De snelheid van een baksteen die in een zwart gat valt

De baksteen nadert de horizon van het zwarte gat,
een kabouter heeft zichzelf gepromoveerd tot meebeweger
door zich aan de baksteen vast te laten ketenen

Ik laat vanaf grote afstand een baksteen in een zwart gat
vallen en een kabouter, met een groen mutsje, heeft zichzelf laten vastketenen aan de baksteen en zichzelf daarmee
tot meebewegende waarnemer [Engels: comoving observer of free falling observer of
rain observer (regendruppels zijn in vrije val als je de luchtweerstand verwaarloost)] gepromoveerd.
Op het plaatje hiernaast zie je de kabouter, die zichzelf vrijwillig gemeld heeft, vastgeketend aan de baksteen.
Wat is de snelheid van de baksteen in zijn referentiekader, zijn referentiestelsel, zijn coördinatenstelsel?
Het simpele antwoord is: nul.
De snelheid van de baksteen in het referentiestelsel van de kabouter is nul komma nul.
Ook al suist de kabouter met toenemende snelheid richting het
zwarte gat, bezien vanuit de achterblijvers, voor de
kabouter beweegt de baksteen niet, hij is immers meebeweger, hij zit er zelfs aan vastgeketend.
Voor de kabouter is het niet anders dan wanneer hij in zijn achtertuin op de baksteen zou zitten, de baksteen is
voor hem in rust en heeft geen snelheid.
Dat de baksteen zich in dit geval ergens in de ruimte bevindt en richting een
zwart gat beweegt is totaal niet relevant.
Sterker nog, dat de baksteen richting een zwart gat
beweegt daar merkt de kabouter helemaal niets van.
Als hem dat vooraf niet verteld was dan zou hij dat zelfs niet weten of merken.
Zweven in de ruimte of richting een zwart gat bewegen
zijn voor de kabouter ononderscheidbaar (zie de pagina over het
equivalentieprincipe).
Oftewel, gedurende het hele traject dat de baksteen aflegt is voor de kabouter de snelheid van de baksteen gelijk
aan nul.
Ook wanneer hij de horizon passeert.
 Deze tabel geldt voor een niet-roterend zwart gat |
 Voor een verre stationaire waarnemer |
 Voor een nabije stationaire waarnemer |
 Voor een meebewegende waarnemer |
| De invaltijd van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
|
| De snelheid van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
Toon uitwerking (= deze pagina) |
| De versnelling van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
Toon uitwerking |
 Door naar het volgende vraagstuk: de naam van een zwart gat
Door naar het volgende vraagstuk: de naam van een zwart gat Terug naar het vorige vraagstuk: de invaltijd van een baksteen die in een zwart gat valt
Terug naar het vorige vraagstuk: de invaltijd van een baksteen die in een zwart gat valt Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie Het equivalentieprincipe
Het equivalentieprincipe Wat maakt een zwart gat tot een zwart gat?
Wat maakt een zwart gat tot een zwart gat? De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van De integralen van
De integralen van Vectoren
Vectoren Vectoren, vraagstuk 40
Vectoren, vraagstuk 40 Vectoren, vraagstuk 85
Vectoren, vraagstuk 85 Taylor-reeksen
Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van De stelling van Green
De stelling van Green Holomorfie van de functie
Holomorfie van de functie Integreren van complexe functies
Integreren van complexe functies Uitleg artikel algemene relativiteitstheorie: paragraaf 13
Uitleg artikel algemene relativiteitstheorie: paragraaf 13 De tweelingparadox
De tweelingparadox De energie van gravitatiestraling
De energie van gravitatiestraling Een dag zonder verjaardagen
Een dag zonder verjaardagen Het vermogen van gravitatiestraling
Het vermogen van gravitatiestraling Tijdsvertraging van een lichtstraal (2e orde benadering)
Tijdsvertraging van een lichtstraal (2e orde benadering)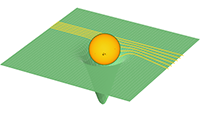 Tijdsvertraging van een lichtstraal (1e orde benadering)
Tijdsvertraging van een lichtstraal (1e orde benadering)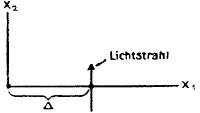 Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein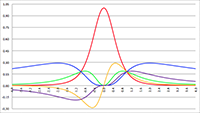 De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen