Tijdsvertraging van een lichtstraal, 2e orde benadering
Bereken de vertraging die een lichtstraal oploopt tijdens het passeren van een massa
(in een tweede orde benadering).
Wanneer een lichtstraal een (significante) massa passeert dan gebeuren er twee dingen:
- de lichtstraal wordt afgebogen,
- de lichtstraal loopt vertraging op.
We gaan ons richten op dat tweede punt, de tijdsvertraging van de lichtstraal.
De lichtstraal loopt natuurlijk niet echt vertraging op, maar vergeleken met een newtoniaanse zienswijze wel
want daar bestaat helemaal geen ruimtetijdkromming.
Ik zal dat even illustreren met een plaatje.

Lichtstralen worden afgebogen wanneer die langs een massa scheren
Ik zal voor de duidelijkheid er nog een lichtstraal aan toevoegen die perfect rechtdoor gaat.

Lichtstralen worden afgebogen wanneer die langs een massa scheren,
de rode lichtstraal gaat rechtdoor
Behalve dat die lichtstralen afgebogen worden moeten ze ook nog door die ‘kuil’ als gevolg van de ruimtetijdkromming
(deze kuil die ik in de plaatjes heb getekend is puur ter illustratie, het is een handige analogie, maar het voegt
een extra dimensie toe die er in werkelijkheid helemaal niet is).
Ik zal het hemellichaam even weghalen zodat dat beter zichtbaar wordt.

Lichtstralen worden afgebogen wanneer die langs een massa scheren
en lopen tijdsvertraging op door de ruimtetijdkromming
Ook hier zal ik er voor de duidelijkheid nog een lichtstraal aan toevoegen die geen tijdsvertraging oploopt
(maar wel afgebogen wordt).

Lichtstralen worden afgebogen wanneer die langs een massa scheren
en lopen tijdsvertraging op door de ruimtetijdkromming,
de rode lichtstraal loopt geen vertraging op
Ik zal de andere lichtstralen weghalen op één na.

De gele lichtstraal wordt afgebogen en loopt tijdsvertraging op,
de rode lichtstraal wordt afgebogen en loopt geen vertraging op
De lichtstraal komt ergens van ‘ver weg’ en de loodrechte afstand van dit begintraject tot een as precies door
het middelpunt van het hemellichaam is de
impactparameter b.

b is de impactparameter, voor grote waarden van b gebeurt er niets,
voor b = 0 heb je een frontale botsing
Ik maak een plaatje van het bovenaanzicht, het punt van dichtste nadering tot het hemellichaam noem ik A.
Op
deze pagina heb ik de vergelijking afgeleid van de lichtstraal:
De lichtstraal komt van ver weg en beweegt richting het hemellichaam, waar zich de oorsprong bevindt, en dus is dr
negatief en moeten we het minteken gebruiken:
Hierin is Rs de Schwarzschild-straal,
de horizon
van een zwart gat:
P is een constante van de beweging:
Die op zijn beurt is opgebouwd uit twee andere constanten van de beweging plus de lichtsnelheid:
De lichtstraal beweegt richting het hemellichaam, dr/dt is dan negatief, bereikt het punt van dichtste nadering waar dr/dt
gelijk aan nul is, en beweegt zich vervolgens weer bij het hemellichaam vandaan, dr/dt is dan positief.
Het punt A is dus een interessant punt, want daar is dr/dt nul:
De linkerterm van het rechterlid kan niet nul worden, want R
s ligt ver binnen het hemellichaam en
dat wordt duidelijk uit onderstaande tabel (R is de straal van het betreffende hemellichaam, voor de gegevens
van de hemellichamen zie de
tabel met fysische gegevens).
| Gerangschikt naar oplopende waarden van Rs/R |
| Hemellichaam: | Rs/R: |

Baksteen | ≈ 0.00000000000000000000000003 = 3 ∙ 10−26 |

Rotsblok van 100 kg,
(diameter = 1 meter) | ≈ 0.0000000000000000000000003 = 3 ∙ 10−25 |

Pluto | 0.0000000000163 = 1.63 ∙ 10−11 |

Maan | 0.0000000000628 = 6.28 ∙ 10−11 |

Mercurius | 0.000000000201 = 2.01 ∙ 10−10 |

Mars | 0.000000000281 = 2.81 ∙ 10−10 |

Venus | 0.00000000119 = 1.19 ∙ 10−9 |

Aarde | 0.00000000139 = 1.39 ∙ 10−9 |

Uranus | 0.00000000504 = 5.04 ∙ 10−9 |

Neptunus | 0.00000000614 = 6.14 ∙ 10−9 |

Saturnus | 0.0000000140 = 1.40 ∙ 10−8 |

Jupiter | 0.0000000394 = 3.94 ∙ 10−8 |

Canis Majoris | ≈ 0.00000005 = 5 ∙ 10−8 |

Betelgeuse | ≈ 0.0000001 = 1 ∙ 10−7 |

Aldebaran | ≈ 0.0000001 = 1 ∙ 10−7 |

Zon | 0.00000425 = 4.25 ∙ 10−6 |

Andromeda | ≈ 0.000006 = 6 ∙ 10−6 |

Witte dwerg | ≈ 0.0005 = 5 ∙ 10−4 |

Neutronenster | ≈ 0.5 = 5 ∙ 10−1 |

Zwart gat | 1 = 1 ∙ 100 |
| (Credits voor de foto’s van de hemellichamen: NASA) |
Vergelijking (6) wordt dan:
In het punt A is de afstand tot de oorsprong r
A:
Dit vul ik in in vergelijking (2):
Vervolgens schrijf ik dit iets anders op:
Nu ga ik beide zijden
integreren met
als
grenzen het beginpunt van de
lichtstraal (r
0, t
0) en het punt A (r
A, t
A):
Het eerste probleem is dat deze
integraal
niet rechtstreeks op te lossen is.
Daar komt nog bij dat de
integrand
oneindig wordt in het punt r = r
A, omdat daar het deel onder het
wortelteken nul wordt
(zie de vergelijkingen (6) en (7)).

De grafiek van f (r), de
integrand,
voor r
A = 2 (de rode lijn),
r
A = 5 (de oranje lijn), r
A = 10 (de groene lijn),
r
A = 20 (de paarse lijn), r
A = 50 (de blauwe lijn)
en r
A = 100 (de grijze lijn), R
s = 1
Ik heb de term met de wortel afgesplitst,
en de breuk die daarvoor staat ga ik ontwikkelen in een Taylor-reeks.
In de tabel met Taylor-reeksen vinden we:
Hiermee wordt vergelijking (11):
Omdat R
s/r heel erg klein is, is (R
s/r)
2 heeeeeeeeeel erg klein en kan ik de
termen met (R
s/r)
3 en hogere ordes verwaarlozen (want ik doe immers een tweede orde benadering).
Dus als ik de eerste drie termen van de reeks meeneem dan ben ik nog steeds goed bezig:
De term met de
wortel zou ik ook kunnen ontwikkelen
in een Taylor-reeks.
In de
tabel met Taylor-reeksen vinden we:
Echter, hiermee kom ik gegarandeerd in de problemen, omdat de
convergentie dan weg is (want het deel onder de
wortel wordt nul).
Daarom voer ik de volgende splitsingstruc uit:
Wat concreter ziet dat er zo uit:
Door de vergelijkingen (14) en (17) te vergelijken vind ik voor a:
Die breuk noem ik voor het gemak (van wat komen gaat) B:
Hiermee kan ik a
2 heel compact schrijven als:
En door nogmaals de vergelijkingen (14) en (17) te vergelijken vind ik voor x:
In de
tabel met gesplitste Taylor-reeksen vinden we
de coëfficiënten c
n:
Ik ga a
2, vergelijking (20), invullen in de coëfficiënten c
n en hogere orde termen
van R
s/r (derde orde en hoger) gooi ik gelijk overboord:
De regelmaat moge duidelijk zijn:
Ik ga B, vergelijking (19), weer invullen:
De term met de
wortel uit vergelijking (14)
neem ik even apart onder handen:
Met behulp van al het voorgaande ga ik nu de splitsing uitvoeren:
Ik breng vergelijking (12) weer even voor het voetlicht:
Hiermee kan ik de eerste - en de derde somreeks wegwerken uit vergelijking (27):
In de
tabel met Taylor-reeksen vinden we ook nog:
Met behulp hiervan kan ik ook de resterende somreeks wegwerken:
Met al deze ingrediënten wordt de
integraal,
vergelijking (14):
Ik ga haakjes wegwerken en hogere orde termen van R
s/r (derde orde en hoger) gooi ik weer overboord:
Ik heb nu zeven
integralen en die werk ik
apart uit.
De oplossing van de
integraal
van x/(x
2 − a
2)
1/2 kun je vinden in de
tabel met integralen.
Daarmee kan ik de eerste
integraal uitwerken:
De oplossing van de
integraal
van 1/((x + a) (x
2 − a
2))
1/2) kun je vinden in de
tabel met integralen.
Daarmee kan ik de tweede
integraal uitwerken:
De oplossing van de
integraal
van 1/((x + a) (x
2 − a
2))
1/2) kun je vinden in de
tabel met integralen en
de oplossing van de
integraal
van 1/((x + a)
2 (x
2 − a
2))
1/2) kun je vinden in de
tabel met integralen.
Daarmee kan ik de derde
integraal uitwerken
(waarbij ik gebruik maak van
breuksplitsing):
De oplossing van de
integraal
van 1/((x + a) (x
2 − a
2))
1/2) kun je vinden in de
tabel met integralen en
de oplossing van de
integraal
van 1/(x (x
2 − a
2)
1/2) kun je vinden in de
tabel met integralen.
Daarmee kan ik de vierde
integraal uitwerken
(waarbij ik weer gebruik maak van
breuksplitsing):
De oplossing van de
integraal
van 1/(x
2 − a
2)
1/2 kun je vinden in de
tabel met integralen.
Daarmee kan ik de vijfde
integraal uitwerken:
De oplossing van de
integraal
van 1/(x (x
2 − a
2)
1/2) kun je vinden in de
tabel met integralen en
de oplossing van de
integraal
van 1/((x + a) (x
2 − a
2))
1/2) kun je vinden in de
tabel met integralen.
Daarmee kan ik de zesde
integraal uitwerken
(waarbij ik nogmaals gebruik maak van
breuksplitsing):
De oplossing van de
integraal
van 1/(x (x
2 − a
2)
1/2) kun je vinden in de
tabel met integralen.
Daarmee kan ik de zevende
integraal uitwerken:
Met al deze deeloplossingen kom ik tot het volgende resultaat:
De eerste term is simpelweg de
stelling van Pythagoras.
Logisch, want newtoniaans bezien is de ruimtetijd vlak.
Het blijkt ook uit het feit dat het de enige term is waar geen Rs in voorkomt.
Ik ben op zoek naar de relativistische vertraging die de lichtstraal oploopt, dus dat is dan het resultaat volgens
vergelijking (34) minus het newtoniaanse resultaat (de eerste term).
Aldus kom ik tot de volgende vertraging, gemeten vanaf het beginpunt (r
0, t
0) tot aan het punt A:
Dan rest nog de taak om r
A te bepalen.
Zoals ik aan het begin al aangaf loopt de lichtstraal vertraging op én de lichtstraal wordt afgebogen.
In een eveneens tweede orde benadering is de afbuigingshoek van de lichtstraal wanneer die het traject doorloopt van
r = −∞ tot r = +∞ (voor de berekening zie
deze pagina):
In het punt A is de afbuigingshoek precies de helft hiervan:
De afbuigingsafstand is dan:
Hieruit volgt voor r
A:
Door vergelijking (39) in te vullen in vergelijking (35) heb ik tenslotte de tijdsvertraging tot aan het punt A als functie van b,
r
0 en R
s.

De grafiek van t
v (b) voor R
s = 1000 (de rode lijn),
R
s = 2000 (de groene lijn) en R
s = 3000 (de blauwe lijn),
c = 299792458, r
0 = 10
11
Ik zal ter illustratie de grafiek combineren met het resultaat van de
eerste orde berekening.

De grafiek van t
v (b), eerste orde (de oranje/paarse/grijze lijnen)
met daaroverheen de grafiek van t
v (b), tweede orde (de rode/groene/blauwe lijnen),
c = 299792458, r
0 = 10
11
De eerste orde grafiek wordt volledig bedekt door de tweede orde grafiek.
Ik laat daarom ook nog het verschil zien tussen de
eerste orde berekening en de tweede orde berekening.

De grafiek van t
v (b) voor R
s = 1000 (de rode lijn),
R
s = 2000 (de groene lijn) en R
s = 3000 (de blauwe lijn),
alleen de tweede orde termen, c = 299792458, r
0 = 10
11































































































 Door naar het volgende vraagstuk: het vermogen van gravitatiestraling
Door naar het volgende vraagstuk: het vermogen van gravitatiestraling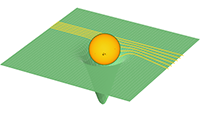 Terug naar het vorige vraagstuk: tijdsvertraging van een lichtstraal, 1e orde benadering
Terug naar het vorige vraagstuk: tijdsvertraging van een lichtstraal, 1e orde benadering Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie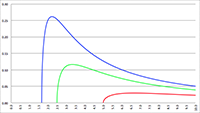 De integraal van
De integraal van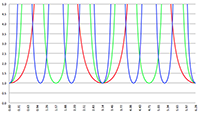 De integraal van
De integraal van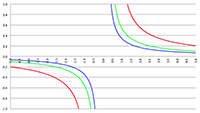 De integraal van
De integraal van De integraal van
De integraal van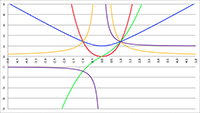 De integralen van
De integralen van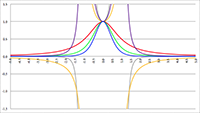 De integralen van
De integralen van Vectoren, vraagstuk 7
Vectoren, vraagstuk 7 Vectoren, vraagstuk 52
Vectoren, vraagstuk 52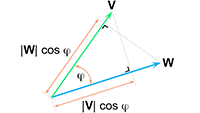 Invariantie van het inwendig product
Invariantie van het inwendig product Taylor-reeksen
Taylor-reeksen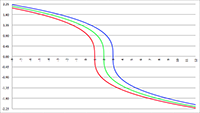 De Taylor-reeks van
De Taylor-reeks van Een reeks afsplitsen van
Een reeks afsplitsen van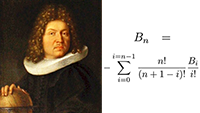 Bernoulli-getallen
Bernoulli-getallen Holomorfie van de functie
Holomorfie van de functie Relativiteitstheorie basic, hoofdstuk 3: het balletje
Relativiteitstheorie basic, hoofdstuk 3: het balletje Uitleg artikel precessie van Mercurius
Uitleg artikel precessie van Mercurius Het relativistische impulsmoment van een holle bol
Het relativistische impulsmoment van een holle bol Een lichtstraal bij een massa
Een lichtstraal bij een massa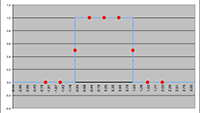 Fourier-analyse van het onzekerheidsprincipe van Heisenberg (I)
Fourier-analyse van het onzekerheidsprincipe van Heisenberg (I) Hoe ziet de wereld er morgen uit?
Hoe ziet de wereld er morgen uit? De tweelingparadox
De tweelingparadox De energie van gravitatiestraling
De energie van gravitatiestraling Een dag zonder verjaardagen
Een dag zonder verjaardagen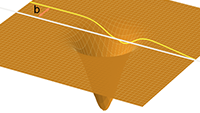 Tijdsvertraging van een lichtstraal (2e orde benadering)
Tijdsvertraging van een lichtstraal (2e orde benadering)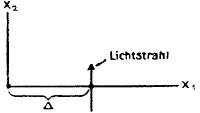 Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein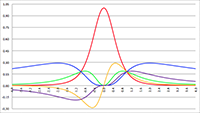 De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen