Wat maakt een zwart gat tot een zwart gat?
Met behulp van de wetten van Newton kun je de ontsnappingssnelheid van een hemellichaam berekenen, de snelheid die nodig is om het oppervlak van dat hemellichaam te verlaten en er nooit meer op terug te vallen:
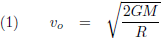

De ontsnappingssnelheid van de Aarde is elf kilometer per seconde,
ook de Space Shuttle haalt dat niet en is dus ongeschikt voor interplanetair reizen
(Credits: NASA)
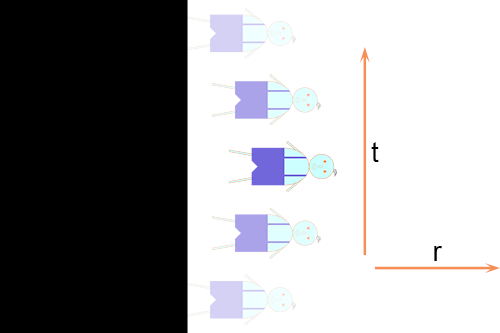
De Engelsman Michell (in de literatuur vaak foutief geschreven als Mitchell) en de Fransman Laplace hadden ruwweg honderd jaar nadat Newton zijn wetten had neergeschreven, onafhankelijk van elkaar, als eersten de overpeinzing hoe het zou zijn indien deze ontsnappingssnelheid de snelheid van het licht zou overschrijden. Michell schreef hier in 1783 over in een brief aan Cavendish en Laplace komt er in 1796 mee voor de dag in zijn boek Exposition du système du Monde. Daarmee was het concept van een donkere ster, een onzichtbare ster, geboren:
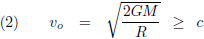
Men had inmiddels al geruimte tijd een aardig idee van de snelheid van het licht door het werk van de Deense astronoom Rømer (in de literatuur vaak foutief geschreven als Römer). Wanneer de manen van de planeet Jupiter achter de planeet langsdraaien (vanaf de Aarde gezien uiteraard) en ze komen op enig moment weer te voorschijn, bleek dat op een enigszins variabel tijdstip te gebeuren. Terwijl andere natuurkundigen, die een verklaring zochten voor de afwijking, zich afvroegen wat er zich bij Jupiter zou kunnen afspelen verplaatste Rømer het probleem naar de Aarde. Deze verandering van gezichtspunt leidde naar de oplossing, want afhankelijk van de positie van de Aarde ten opzichte van Jupiter verandert de weglengte die het licht moet afleggen, in het uiterste geval is het verschil de diameter van de aardbaan. Deel de diameter van de aardbaan (300 miljoen kilometer) door het verschil in uiterste tijdstippen dat de manen van Jupiter zichtbaar worden (bijna zeventien minuten) en je hebt de lichtsnelheid: 300.000 kilometer per seconde. De oplossing is altijd simpel en Rømer zat er, in 1676, maar een procent of twintig naast.

Rømer gebruikte de verschijning van de maan Io (bij de pijl) als ijkpunt voor zijn metingen,
links staan de oorspronkelijke aantekeningen van Rømer
(Io is voor de duidelijkheid overdreven groot weergegeven)

De lichtsnelheid is de diameter van de aardbaan gedeeld door het verschil
in uiterste tijdstippen dat de manen van Jupiter zichtbaar worden
(niet op schaal weergegeven)
| Metaal | Dichtheid [kg/m3] |
Diameter [m] |
Diameter/diameter Zon | Massa [kg] |
Massa/massa Zon |
| Goud | 19320 | 1.824 ∙ 1011 | 131 | 6.141 ∙ 1037 | 3.087 ∙ 107 |
| Lood | 11340 | 2.381 ∙ 1011 | 171 | 8.016 ∙ 1037 | 4.030 ∙ 107 |
| Platina | 21450 | 1.731 ∙ 1011 | 124 | 5.828 ∙ 1037 | 2.930 ∙ 107 |
Het onderwerp verdwijnt naar de achtergrond, maar ruim honderd jaar later verschijnt het opnieuw op de radar wanneer de Duitser Schwarzschild eind 1915 (in de literatuur vaak foutief genoemd als 1916) de eerste exacte oplossing vindt voor de vergelijkingen van de algemene relativiteitstheorie, de Schwarzschild-oplossing:
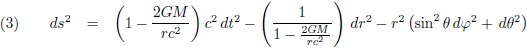
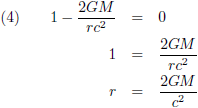
En dit komt overeen met de vergelijkingen (1) en (2): de straal van een massa met een ontsnappingssnelheid gelijk aan de lichtsnelheid. Velen, te beginnen met Einstein zelf, zagen dit als een wiskundig akkefietje. Bovendien was algemene relativiteitstheorie verre van een ‘hot topic’ in die dagen, het verklaarde de periheliumprecessie van Mercurius en daarmee was alles wel zo’n beetje uitgewerkt voor wat betreft het praktische nut. Kwantummechanica en deeltjesfysica, daar gebeurde het!
We maken weer een sprong voorwaarts in de tijd, ditmaal een halve eeuw, en dan begint algemene relativiteitstheorie eindelijk de aandacht te krijgen die het verdient. Langzaam maar zeker dringt het besef door dat Moeder Natuur daadwerkelijk objecten creëert waarbij alle massa is samengeperst binnen de afstand:
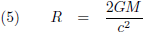
Ondanks de overeenkomsten tussen de vergelijkingen (1), (2), (4) en (5) verschilt de donkere ster van Michell en Laplace, een newtoniaanse zienswijze, fundamenteel van een zwart gat, de relativistische zienswijze. Ik ga dat illustreren aan de hand van een massa van 1.55 biljoen zonsmassa’s. De afstand tot het centrum waarbij de ontsnappingssnelheid gelijk is aan de lichtsnelheid is R = 4.579 ∙ 1015 m. De valversnelling bij die afstand is g = 9.81 m/s2, dus gelijk aan hier op Aarde.
Stel dat de massa zich precies uitstrekt tot aan de afstand R, dan zou een persoon daar gewoon kunnen staan net als op Aarde. Ik heb daar een ruimtetijddiagram van gemaakt, zie het plaatje hiernaast. Horizontaal is de ruimtelijke coördinaat r uitgezet en verticaal de tijd t. Het zwarte vlak is de graviterende massa.
Ik kan de wereldlijn van deze persoon erbij intekenen, de groene lijn, en de bijbehorende lichtkegel. De lichtkegel is weliswaar een relativistisch ingrediënt, maar dat neemt niet weg dat deze persoon zowel newtoniaans als relativistisch kan doen en laten wat hij wil binnen de grenzen van de lichtkegel.
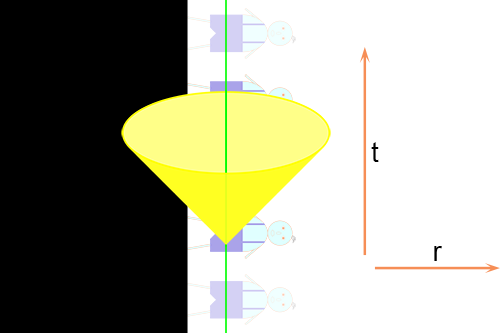
Hij zou bijvoorbeeld een sprongetje kunnen maken ondanks het feit dat de ontsnappingssnelheid gelijk is aan de lichtsnelheid. Vergelijk het met de Aarde, die heeft een ontsnappingssnelheid van ruim elf kilometer per seconde maar dat weerhoudt mij er niet van om te kunnen springen (ook al ontwikkel ik natuurlijk in de verste verte geen snelheid van elf kilometer per seconde).

Ook al ontwikkelt een mens maar een fractie van de ontsnappingssnelheid,
daarom kan een mens nog wel springen
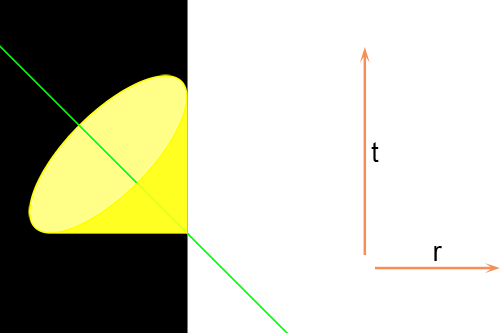
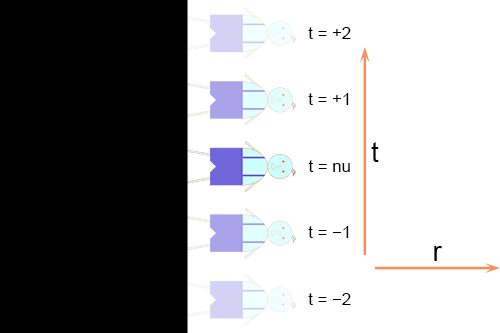
Hoe anders is de situatie vanuit een relativistisch oogpunt. Door de kromming van de ruimtetijd is de lichtkegel gekanteld. De centrale as van de lichtkegel representeert de actie “ik doe niets” en die leidt onvermijdelijk naar het middelpunt van het zwarte gat.

Zelfs indien de persoon in kwestie alle hypothetische zeilen bijzet en de lichtsnelheid ontwikkelt is het beste dat hij kan bereiken zich handhaven aan de rand van het zwarte gat (de groene lijn). Omdat de lichtsnelheid de maximale snelheid is kan hij alleen bewegen binnen de lichtkegel en is het verlaten van het zwarte gat geen optie: de natuurkundewetten verbieden het. Is dat ook wiskundig te onderbouwen? Uiteraard.
Middels de volgende transformatie ga ik de Schwarzschild-oplossing omschrijven naar Eddington-Finkelstein-coördinaten:
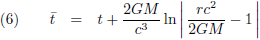
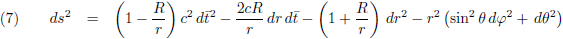
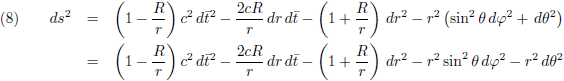
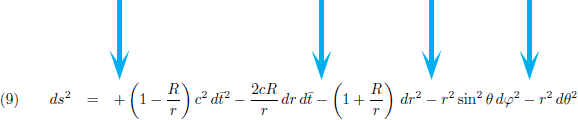
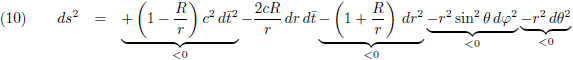
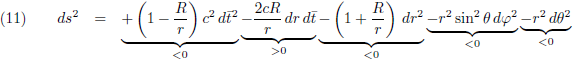
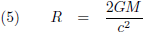

In twee dimensies zou je de kromming van de vierdimensionale ruimtetijd kunnen weergeven
als een trechter waarbij je voorbij een bepaald punt (r = R = de blauwe lijn = de horizon)
niet anders meer kunt dan verder de trechter in, voortgedreven door de tijd










 Door naar het volgende vraagstuk: de race tegen de lichtstraal
Door naar het volgende vraagstuk: de race tegen de lichtstraal Terug naar het vorige vraagstuk: de Ricci-scalar van de Schwarzschild-metriek
Terug naar het vorige vraagstuk: de Ricci-scalar van de Schwarzschild-metriek Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie Uitleg artikel algemene relativiteitstheorie
Uitleg artikel algemene relativiteitstheorie De ontsnappingssnelheid
De ontsnappingssnelheid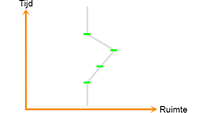 Het tekenen van een wereldlijn
Het tekenen van een wereldlijn Afleiding van de Schwarzschild-oplossing
Afleiding van de Schwarzschild-oplossing Stabiliteit van cirkelvormige banen om een centrale massa
Stabiliteit van cirkelvormige banen om een centrale massa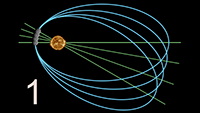 Relativistische periheliumprecessie, 1e orde benadering
Relativistische periheliumprecessie, 1e orde benadering Eddington-Finkelstein-coördinaten
Eddington-Finkelstein-coördinaten De maximale snelheid
De maximale snelheid De Schwarzschild-metriek in isotrope coördinaten
De Schwarzschild-metriek in isotrope coördinaten De Schwarzschild-oplossing van de algemene relativiteitstheorie
De Schwarzschild-oplossing van de algemene relativiteitstheorie Klassieke periheliumprecessie
Klassieke periheliumprecessie Periheliumprecessie als gevolg van een oblate ster
Periheliumprecessie als gevolg van een oblate ster Zou je als kind geïnspireerd zijn?
Zou je als kind geïnspireerd zijn? De illusie dat ik milieubewust ben
De illusie dat ik milieubewust ben De reis naar de werkelijkheid van Carl Jung
De reis naar de werkelijkheid van Carl Jung De Natuur spreekt: Mother Nature/Moeder Natuur
De Natuur spreekt: Mother Nature/Moeder Natuur De integraal van
De integraal van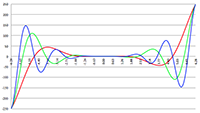 De integraal van
De integraal van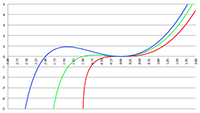 De integraal van
De integraal van De contourintegraal van
De contourintegraal van Afbuiging van een lichtstraal (2e orde benadering)
Afbuiging van een lichtstraal (2e orde benadering) Afbuiging van een lichtstraal (1e orde benadering)
Afbuiging van een lichtstraal (1e orde benadering) Bewerkingen met reeksen
Bewerkingen met reeksen De Taylor-reeksen van
De Taylor-reeksen van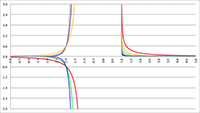 De integralen van
De integralen van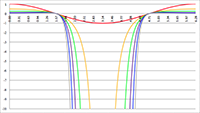 De integralen van
De integralen van De integralen van
De integralen van De massa van de atmosfeer
De massa van de atmosfeer Hyper-Catalan-getallen
Hyper-Catalan-getallen Een ontmoeting met aliens
Een ontmoeting met aliens Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen