Een dag zonder verjaardagen
Hoe groot is de kans dat er op minstens één dag in het jaar niemand op Aarde jarig is?
Ga ervanuit dat een jaar 365 dagen heeft en dat er acht miljard mensen op Aarde zijn.

Één dag in het jaar geen verjaardag...
Wanneer er drie dagen in een jaar zitten en er is maar één mens op Aarde dan is die ene mens uiteraard op één van die drie dagen jarig. Die drie mogelijkheden noem ik combinaties en ik nummer de dagen als 1, 2, 3. In een tabel ziet dat er als volgt uit:
| Combinaties |
| 1 |
| 2 |
| 3 |
| Combinaties |
| 11 |
| 12 |
| 13 |
| 21 |
| 22 |
| 23 |
| 31 |
| 32 |
| 33 |
| Combinaties |
| 111 |
| 112 |
| 113 |
| 121 |
| 122 |
| 123 |
| 131 |
| 132 |
| 133 |
| 211 |
| 212 |
| 213 |
| 221 |
| 222 |
| 223 |
| 231 |
| 232 |
| 233 |
| 311 |
| 312 |
| 313 |
| 321 |
| 322 |
| 323 |
| 331 |
| 332 |
| 333 |
| Combinaties | Kolom0: nul dagen niemand jarig |
Kolom1: één dag niemand jarig |
Kolom2: twee dagen niemand jarig |
| 111 | 1 | ||
| 112 | 1 | ||
| 113 | 1 | ||
| 121 | 1 | ||
| 122 | 1 | ||
| 123 | 1 | ||
| 131 | 1 | ||
| 132 | 1 | ||
| 133 | 1 | ||
| 211 | 1 | ||
| 212 | 1 | ||
| 213 | 1 | ||
| 221 | 1 | ||
| 222 | 1 | ||
| 223 | 1 | ||
| 231 | 1 | ||
| 232 | 1 | ||
| 233 | 1 | ||
| 311 | 1 | ||
| 312 | 1 | ||
| 313 | 1 | ||
| 321 | 1 | ||
| 322 | 1 | ||
| 323 | 1 | ||
| 331 | 1 | ||
| 332 | 1 | ||
| 333 | 1 | ||
| 27 | 6 | 18 | 3 |
| Combinaties | Kolom0: nul dagen niemand jarig |
Kolom1: één dag niemand jarig |
Kolom2: twee dagen niemand jarig |
| 1111 | 1 | ||
| 1112 | 1 | ||
| 1113 | 1 | ||
| 1121 | 1 | ||
| 1122 | 1 | ||
| 1123 | 1 | ||
| 1131 | 1 | ||
| 1132 | 1 | ||
| 1133 | 1 | ||
| 1211 | 1 | ||
| 1212 | 1 | ||
| 1213 | 1 | ||
| 1221 | 1 | ||
| 1222 | 1 | ||
| 1223 | 1 | ||
| 1231 | 1 | ||
| 1232 | 1 | ||
| 1233 | 1 | ||
| 1311 | 1 | ||
| 1312 | 1 | ||
| 1313 | 1 | ||
| 1321 | 1 | ||
| 1322 | 1 | ||
| 1323 | 1 | ||
| 1331 | 1 | ||
| 1332 | 1 | ||
| 1333 | 1 | ||
| 2111 | 1 | ||
| 2112 | 1 | ||
| 2113 | 1 | ||
| 2121 | 1 | ||
| 2122 | 1 | ||
| 2123 | 1 | ||
| 2131 | 1 | ||
| 2132 | 1 | ||
| 2133 | 1 | ||
| 2211 | 1 | ||
| 2212 | 1 | ||
| 2213 | 1 | ||
| 2221 | 1 | ||
| 2222 | 1 | ||
| 2223 | 1 | ||
| 2231 | 1 | ||
| 2232 | 1 | ||
| 2233 | 1 | ||
| 2311 | 1 | ||
| 2312 | 1 | ||
| 2313 | 1 | ||
| 2321 | 1 | ||
| 2322 | 1 | ||
| 2323 | 1 | ||
| 2331 | 1 | ||
| 2332 | 1 | ||
| 2333 | 1 | ||
| 3111 | 1 | ||
| 3112 | 1 | ||
| 3113 | 1 | ||
| 3121 | 1 | ||
| 3122 | 1 | ||
| 3123 | 1 | ||
| 3131 | 1 | ||
| 3132 | 1 | ||
| 3133 | 1 | ||
| 3211 | 1 | ||
| 3212 | 1 | ||
| 3213 | 1 | ||
| 3221 | 1 | ||
| 3222 | 1 | ||
| 3223 | 1 | ||
| 3231 | 1 | ||
| 3232 | 1 | ||
| 3233 | 1 | ||
| 3311 | 1 | ||
| 3312 | 1 | ||
| 3313 | 1 | ||
| 3321 | 1 | ||
| 3322 | 1 | ||
| 3323 | 1 | ||
| 3331 | 1 | ||
| 3332 | 1 | ||
| 3333 | 1 | ||
| 81 | 36 | 42 | 3 |
| Combinaties | Kolom0: nul dagen niemand jarig |
Kolom1: één dag niemand jarig |
Kolom2: twee dagen niemand jarig |
| 11111 | 1 | ||
| 11112 | 1 | ||
| 11113 | 1 | ||
| 11121 | 1 | ||
| 11122 | 1 | ||
| 11123 | 1 | ||
| 11131 | 1 | ||
| 11132 | 1 | ||
| 11133 | 1 | ||
| 11211 | 1 | ||
| 11212 | 1 | ||
| 11213 | 1 | ||
| 11221 | 1 | ||
| 11222 | 1 | ||
| 11223 | 1 | ||
| 11231 | 1 | ||
| 11232 | 1 | ||
| 11233 | 1 | ||
| 11311 | 1 | ||
| 11312 | 1 | ||
| 11313 | 1 | ||
| 11321 | 1 | ||
| 11322 | 1 | ||
| 11323 | 1 | ||
| 11331 | 1 | ||
| 11332 | 1 | ||
| 11333 | 1 | ||
| 12111 | 1 | ||
| 12112 | 1 | ||
| 12113 | 1 | ||
| 12121 | 1 | ||
| 12122 | 1 | ||
| 12123 | 1 | ||
| 12131 | 1 | ||
| 12132 | 1 | ||
| 12133 | 1 | ||
| 12211 | 1 | ||
| 12212 | 1 | ||
| 12213 | 1 | ||
| 12221 | 1 | ||
| 12222 | 1 | ||
| 12223 | 1 | ||
| 12231 | 1 | ||
| 12232 | 1 | ||
| 12233 | 1 | ||
| 12311 | 1 | ||
| 12312 | 1 | ||
| 12313 | 1 | ||
| 12321 | 1 | ||
| 12322 | 1 | ||
| 12323 | 1 | ||
| 12331 | 1 | ||
| 12332 | 1 | ||
| 12333 | 1 | ||
| 13111 | 1 | ||
| 13112 | 1 | ||
| 13113 | 1 | ||
| 13121 | 1 | ||
| 13122 | 1 | ||
| 13123 | 1 | ||
| 13131 | 1 | ||
| 13132 | 1 | ||
| 13133 | 1 | ||
| 13211 | 1 | ||
| 13212 | 1 | ||
| 13213 | 1 | ||
| 13221 | 1 | ||
| 13222 | 1 | ||
| 13223 | 1 | ||
| 13231 | 1 | ||
| 13232 | 1 | ||
| 13233 | 1 | ||
| 13311 | 1 | ||
| 13312 | 1 | ||
| 13313 | 1 | ||
| 13321 | 1 | ||
| 13322 | 1 | ||
| 13323 | 1 | ||
| 13331 | 1 | ||
| 13332 | 1 | ||
| 13333 | 1 | ||
| 21111 | 1 | ||
| 21112 | 1 | ||
| 21113 | 1 | ||
| 21121 | 1 | ||
| 21122 | 1 | ||
| 21123 | 1 | ||
| 21131 | 1 | ||
| 21132 | 1 | ||
| 21133 | 1 | ||
| 21211 | 1 | ||
| 21212 | 1 | ||
| 21213 | 1 | ||
| 21221 | 1 | ||
| 21222 | 1 | ||
| 21223 | 1 | ||
| 21231 | 1 | ||
| 21232 | 1 | ||
| 21233 | 1 | ||
| 21311 | 1 | ||
| 21312 | 1 | ||
| 21313 | 1 | ||
| 21321 | 1 | ||
| 21322 | 1 | ||
| 21323 | 1 | ||
| 21331 | 1 | ||
| 21332 | 1 | ||
| 21333 | 1 | ||
| 22111 | 1 | ||
| 22112 | 1 | ||
| 22113 | 1 | ||
| 22121 | 1 | ||
| 22122 | 1 | ||
| 22123 | 1 | ||
| 22131 | 1 | ||
| 22132 | 1 | ||
| 22133 | 1 | ||
| 22211 | 1 | ||
| 22212 | 1 | ||
| 22213 | 1 | ||
| 22221 | 1 | ||
| 22222 | 1 | ||
| 22223 | 1 | ||
| 22231 | 1 | ||
| 22232 | 1 | ||
| 22233 | 1 | ||
| 22311 | 1 | ||
| 22312 | 1 | ||
| 22313 | 1 | ||
| 22321 | 1 | ||
| 22322 | 1 | ||
| 22323 | 1 | ||
| 22331 | 1 | ||
| 22332 | 1 | ||
| 22333 | 1 | ||
| 23111 | 1 | ||
| 23112 | 1 | ||
| 23113 | 1 | ||
| 23121 | 1 | ||
| 23122 | 1 | ||
| 23123 | 1 | ||
| 23131 | 1 | ||
| 23132 | 1 | ||
| 23133 | 1 | ||
| 23211 | 1 | ||
| 23212 | 1 | ||
| 23213 | 1 | ||
| 23221 | 1 | ||
| 23222 | 1 | ||
| 23223 | 1 | ||
| 23231 | 1 | ||
| 23232 | 1 | ||
| 23233 | 1 | ||
| 23311 | 1 | ||
| 23312 | 1 | ||
| 23313 | 1 | ||
| 23321 | 1 | ||
| 23322 | 1 | ||
| 23323 | 1 | ||
| 23331 | 1 | ||
| 23332 | 1 | ||
| 23333 | 1 | ||
| 31111 | 1 | ||
| 31112 | 1 | ||
| 31113 | 1 | ||
| 31121 | 1 | ||
| 31122 | 1 | ||
| 31123 | 1 | ||
| 31131 | 1 | ||
| 31132 | 1 | ||
| 31133 | 1 | ||
| 31211 | 1 | ||
| 31212 | 1 | ||
| 31213 | 1 | ||
| 31221 | 1 | ||
| 31222 | 1 | ||
| 31223 | 1 | ||
| 31231 | 1 | ||
| 31232 | 1 | ||
| 31233 | 1 | ||
| 31311 | 1 | ||
| 31312 | 1 | ||
| 31313 | 1 | ||
| 31321 | 1 | ||
| 31322 | 1 | ||
| 31323 | 1 | ||
| 31331 | 1 | ||
| 31332 | 1 | ||
| 31333 | 1 | ||
| 32111 | 1 | ||
| 32112 | 1 | ||
| 32113 | 1 | ||
| 32121 | 1 | ||
| 32122 | 1 | ||
| 32123 | 1 | ||
| 32131 | 1 | ||
| 32132 | 1 | ||
| 32133 | 1 | ||
| 32211 | 1 | ||
| 32212 | 1 | ||
| 32213 | 1 | ||
| 32221 | 1 | ||
| 32222 | 1 | ||
| 32223 | 1 | ||
| 32231 | 1 | ||
| 32232 | 1 | ||
| 32233 | 1 | ||
| 32311 | 1 | ||
| 32312 | 1 | ||
| 32313 | 1 | ||
| 32321 | 1 | ||
| 32322 | 1 | ||
| 32323 | 1 | ||
| 32331 | 1 | ||
| 32332 | 1 | ||
| 32333 | 1 | ||
| 33111 | 1 | ||
| 33112 | 1 | ||
| 33113 | 1 | ||
| 33121 | 1 | ||
| 33122 | 1 | ||
| 33123 | 1 | ||
| 33131 | 1 | ||
| 33132 | 1 | ||
| 33133 | 1 | ||
| 33211 | 1 | ||
| 33212 | 1 | ||
| 33213 | 1 | ||
| 33221 | 1 | ||
| 33222 | 1 | ||
| 33223 | 1 | ||
| 33231 | 1 | ||
| 33232 | 1 | ||
| 33233 | 1 | ||
| 33311 | 1 | ||
| 33312 | 1 | ||
| 33313 | 1 | ||
| 33321 | 1 | ||
| 33322 | 1 | ||
| 33323 | 1 | ||
| 33331 | 1 | ||
| 33332 | 1 | ||
| 33333 | 1 | ||
| 243 | 150 | 90 | 3 |
| Aantal mensen |
Aantal combinaties |
Kolom0: nul dagen niemand jarig |
Kolom1: één dag niemand jarig |
Kolom2: twee dagen niemand jarig |
| 1 | 3 | 0 | 0 | 3 |
| 2 | 9 | 0 | 6 | 3 |
| 3 | 27 | 6 | 18 | 3 |
| 4 | 81 | 36 | 42 | 3 |
| 5 | 243 | 150 | 90 | 3 |
- gaan er nul eentjes naar links indien ze in kolom0 staan,
- gaat er één eentje naar links indien ze in kolom1 staan,
- gaan er twee eentjes naar links indien ze in kolom2 staan.
| Aantal mensen = n |
Aantal combinaties = c |
Kolom0: nul dagen niemand jarig = k0 |
Kolom1: één dag niemand jarig = k1 |
Kolom2: twee dagen niemand jarig = k2 |
| 1 | 3 = 31 | 0 | 0 | 3 |
| 2 | 9 = 32 | 0 | 6 | 3 |
| 3 | 27 = 33 | 6 | 18 | 3 |
| 4 | 81 = 34 | 36 | 42 | 3 |
| 5 | 243 = 35 | 150 | 90 | 3 |
 |  |
 |  |
 |
 |  |
 |  |
 |
| Aantal mensen = n |
Aantal combinaties = c |
Kolom0: nul dagen niemand jarig = k0 |
Kolom1: één dag niemand jarig = k1 |
Kolom2: twee dagen niemand jarig = k2 |
| 1 | 3 | 0 | 0 | 3 |
| 2 | 9 | 0 | 6 | 3 |
| 3 | 27 | 6 | 18 | 3 |
| 4 | 81 | 36 | 42 | 3 |
| 5 | 243 | 150 | 90 | 3 |
| 6 | 729 | 540 | 186 | 3 |
| 7 | 2187 | 1806 | 378 | 3 |
| 8 | 6561 | 5796 | 762 | 3 |
| 9 | 19683 | 18150 | 1530 | 3 |
| 10 | 59049 | 55980 | 3066 | 3 |
 |  |
 |  |
 |
 |  |
 |  |
 |

| Aantal mensen = n |
Aantal combinaties = c |
Kolom0: nul dagen niemand jarig = k0 |
Kans = K |
| 1 | 3 | 0 | 1.00000 |
| 2 | 9 | 0 | 1.00000 |
| 3 | 27 | 6 | 0.77778 |
| 4 | 81 | 36 | 0.55556 |
| 5 | 243 | 150 | 0.38272 |
| 6 | 729 | 540 | 0.25926 |
| 7 | 2187 | 1806 | 0.17421 |
| 8 | 6561 | 5796 | 0.11660 |
| 9 | 19683 | 18150 | 0.07788 |
| 10 | 59049 | 55980 | 0.05197 |
| Aantal mensen = n |
Aantal combinaties = c |
Kolom0: nul dagen niemand jarig = k0 |
Kans = K |
| 1 | 3 | 0 | 1.00000 |
| 2 | 9 | 0 | 1.00000 |
| 3 | 27 | 6 | 0.77778 |
| 4 | 81 | 36 | 0.55556 |
| 5 | 243 | 150 | 0.38272 |
| 6 | 729 | 540 | 0.25926 |
| 7 | 2187 | 1806 | 0.17421 |
| 8 | 6561 | 5796 | 0.11660 |
| 9 | 19683 | 18150 | 0.07788 |
| 10 | 59049 | 55980 | 0.05197 |
| 11 | 177147 | 171006 | 0.03467 |
| 12 | 531441 | 519156 | 0.02312 |
| 13 | 1594323 | 1569750 | 0.01541 |
| 14 | 4782969 | 4733820 | 0.01028 |
| 15 | 14348907 | 14250606 | 0.00685 |
| 16 | 43046721 | 42850116 | 0.00457 |
| 17 | 129140163 | 128746950 | 0.00304 |
| 18 | 387420489 | 386634060 | 0.00203 |
| 19 | 1162261467 | 1160688606 | 0.00135 |
| 20 | 3486784401 | 3483638676 | 0.00090 |
| 21 | 10460353203 | 10454061750 | 0.00060 |
| 22 | 31381059609 | 31368476700 | 0.00040 |
| 23 | 94143178827 | 94118013006 | 0.00027 |
| 24 | 282429536481 | 282379204836 | 0.00018 |
| 25 | 847288609443 | 847187946150 | 0.00012 |
| 26 | 2541865828329 | 2541664501740 | 0.00008 |
| 27 | 7625597484987 | 7625194831806 | 0.00005 |
| 28 | 22876792454961 | 22875987148596 | 0.00004 |
| 29 | 68630377364883 | 68628766752150 | 0.00002 |
| 30 | 205891132094649 | 205887910869180 | 0.00002 |
| 31 | 617673396283947 | 617666953833006 | 0.00001 |
| 32 | 1853020188851841 | 1853007303949956 | 0.00001 |
| 33 | 5559060566555523 | 5559034796751750 | 0.00000 |
| Aantal mensen = n |
Aantal combinaties = c |
Kolom0: nul dagen niemand jarig = k0 |
Kolom1: één dag niemand jarig = k1 |
Kolom2: twee dagen niemand jarig = k2 |
| 1 | 3 | 0 | 0 | 3 |
| 2 | 9 | 0 | 6 | 3 |
| 3 | 27 | 6 | 18 | 3 |
| 4 | 81 | 36 | 42 | 3 |
| 5 | 243 | 150 | 90 | 3 |
| 6 | 729 | 540 | 186 | 3 |
| 7 | 2187 | 1806 | 378 | 3 |
| 8 | 6561 | 5796 | 762 | 3 |
| 9 | 19683 | 18150 | 1530 | 3 |
| 10 | 59049 | 55980 | 3066 | 3 |
 |  |
 |  |
 |
 |  |
 |  |
 |
| Aantal mensen = n |
Aantal combinaties = c |
Kolom0: nul dagen niemand jarig = k0 |
Kolom1: één dag niemand jarig = k1 |
Kolom2: twee dagen niemand jarig = k2 |
| 1 | 1 | 0.00000 | 0.00000 | 1.00000 |
| 2 | 1 | 0.00000 | 0.66667 | 0.33333 |
| 3 | 1 | 0.22222 | 0.66667 | 0.11111 |
| 4 | 1 | 0.44444 | 0.51852 | 0.03704 |
| 5 | 1 | 0.61728 | 0.37037 | 0.01235 |
| 6 | 1 | 0.74074 | 0.25514 | 0.00412 |
| 7 | 1 | 0.82579 | 0.17284 | 0.00137 |
| 8 | 1 | 0.88340 | 0.11614 | 0.00046 |
| 9 | 1 | 0.92212 | 0.07773 | 0.00015 |
| 10 | 1 | 0.94803 | 0.05192 | 0.00005 |
 |  |
 |  |
 |
 |  |
 |  |
 |
| Aantal mensen = n |
Kolom0: nul dagen niemand jarig = k0 |
Kolom1: één dag niemand jarig = k1 |
Kolom2: twee dagen niemand jarig = k2 |
 |
Kolom364: 364 dagen niemand jarig = k364 |
| 1 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 1.0000000000 ∙ 100 |
| 2 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 2.7397260274 ∙ 10−3 |
| 3 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 7.5060987052 ∙ 10−6 |
| 4 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 2.0564653987 ∙ 10−8 |
| 5 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 5.6341517772 ∙ 10−11 |
| 6 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 1.5436032266 ∙ 10−13 |
| 7 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 4.2290499360 ∙ 10−16 |
| 8 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 1.1586438181 ∙ 10−18 |
| 9 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 3.1743666249 ∙ 10−21 |
| 10 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 8.6968948627 ∙ 10−24 |
| 20 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 2.0722186370 ∙ 10−49 |
| 50 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 2.8031713233 ∙ 10−126 |
| 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 2.1528135528 ∙ 10−254 |
| 200 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 | 0.0000000000 ∙ 100 |  | 1.2697551214 ∙ 10−510 |
| 364 | 0.0000000000 ∙ 100 | 5.3105865370 ∙ 10−155 | 1.7542460508 ∙ 10−150 |  | 7.7212960109 ∙ 10−931 |
| 365 | 1.4549552156 ∙ 10−157 | 9.6652674974 ∙ 10−153 | 1.5934401628 ∙ 10−148 |  | 2.1154235646 ∙ 10−933 |
| 366 | 2.6625680446 ∙ 10−155 | 8.8275668473 ∙ 10−151 | 9.6844619110 ∙ 10−147 |  | 5.7956809990 ∙ 10−936 |
| 500 | 9.8026681438 ∙ 10−70 | 3.7393395217 ∙ 10−67 | 7.0234614296 ∙ 10−65 |  | 2.6053173774 ∙ 10−1279 |
| 1000 | 1.7123209304 ∙ 10−12 | 5.4431049243 ∙ 10−11 | 8.5445507611 ∙ 10−10 |  | 1.8596379827 ∙ 10−2560 |
| 2000 | 2.1611945163 ∙ 10−1 | 3.3566254507 ∙ 10−1 | 2.5596478898 ∙ 10−1 |  | 9.4746669229 ∙ 10−5123 |
| 5000 | 9.9959746387 ∙ 10−1 | 4.0245831990 ∙ 10−4 | 7.7804717399 ∙ 10−8 |  | 1.2530562935 ∙ 10−12809 |
| 10000 | 9.9999999956 ∙ 10−1 | 4.4410410763 ∙ 10−10 | 9.1194794422 ∙ 10−20 |  | 4.3017810263 ∙ 10−25621 |
| 20000 | 1.0000000000 ∙ 100 | 5.4035194130 ∙ 10−22 | 1.2519178889 ∙ 10−43 |  | 5.0699506845 ∙ 10−51244 |
| 50000 | 1.0000000000 ∙ 100 | 9.7331293159 ∙ 10−58 | 3.2388678928 ∙ 10−115 |  | 8.2998461226 ∙ 10−128113 |
| 99998 | 1.0000000000 ∙ 100 | 2.6097270327 ∙ 10−117 | 1.5965947434 ∙ 10−234 |  | 2.5143917665 ∙ 10−256222 |
| 99999 | 1.0000000000 ∙ 100 | 2.6025770956 ∙ 10−117 | 1.5878462790 ∙ 10−234 |  | 6.8887445658 ∙ 10−256225 |
| 100000 | 1.0000000000 ∙ 100 | 2.5954467474 ∙ 10−117 | 1.5791457515 ∙ 10−234 |  | 1.8873272783 ∙ 10−256227 |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Echter, wanneer we goed kijken naar de bovenstaande tabel dan zien we dat in de laatste regel Kolom1 gigantisch veel kleiner is dan Kolom0, en Kolom2 is vervolgens gigantisch veel kleiner dan Kolom1, enzovoort. Kolom0 geeft de kans aan dat er iedere dag iemand jarig is, en de som van alle overige kolommen geeft de kans aan dat er op minstens één dag niemand jarig is. Maar als de kolommen Kolom2 tot en met Kolom364 in het niet vallen bij Kolom1, dan wordt de kans die we zoeken dus volledig bepaald door Kolom1 (tenzij je een nauwkeurigheid wilt van vele miljoenen significante cijfers, maar dat willen we niet). Het is wel boeiend om te zien hoe de kansverdeling zich door de kolommen verplaatst bij toenemende waarden van n. In onderstaande grafiek is horizontaal de nummering van de kolommen uitgezet, en verticaal de kans van die 365 verschillende kolommen voor verschillende waarden van n.

De grafiek van ki voor n = 1 (de rode lijn),
n = 10 (de lichtgroene lijn), n = 50 (de oranje lijn),
n = 100 (de paarse lijn), n = 200 (de blauwe lijn),
n = 365 (de grijze lijn), n = 500 (de bruine lijn),
n = 1000 (de lichtbruine lijn), n = 2000 (de donkergroene lijn),
n = 5000 (de gele lijn) en n = 10000 (de lichtblauwe lijn)

Het is vanaf hier een balletjesprobleem





Laten we het blijven beschouwen als balletjesprobleem, dus één bijzonder balletje mag niet gepakt worden. Echter, aan het begin is er nog helemaal geen bijzonder balletje, dus dat bijzondere balletje kan op 365 manieren ontstaan. Daarom moet het laatste sommetje nog met 365 vermenigvuldigd worden om tot een goed antwoord te komen:



| Aantal mensen | K1 | K2 |
| 1 | 1.0000000000 ∙ 100 | 3.6400000000 ∙ 102 |
| 2 | 1.0000000000 ∙ 100 | 3.6300273973 ∙ 102 |
| 3 | 1.0000000000 ∙ 100 | 3.6200821167 ∙ 102 |
| 4 | 1.0000000000 ∙ 100 | 3.6101640835 ∙ 102 |
| 5 | 1.0000000000 ∙ 100 | 3.6002732230 ∙ 102 |
| 6 | 1.0000000000 ∙ 100 | 3.5904094608 ∙ 102 |
| 7 | 1.0000000000 ∙ 100 | 3.5805727225 ∙ 102 |
| 8 | 1.0000000000 ∙ 100 | 3.5707629342 ∙ 102 |
| 9 | 1.0000000000 ∙ 100 | 3.5609800221 ∙ 102 |
| 10 | 1.0000000000 ∙ 100 | 3.5512239124 ∙ 102 |
| 20 | 1.0000000000 ∙ 100 | 3.4551208976 ∙ 102 |
| 50 | 1.0000000000 ∙ 100 | 3.1821366393 ∙ 102 |
| 100 | 1.0000000000 ∙ 100 | 2.7742448194 ∙ 102 |
| 200 | 1.0000000000 ∙ 100 | 2.1086121420 ∙ 102 |
| 364 | 1.0000000000 ∙ 100 | 1.3446023023 ∙ 102 |
| 365 | 1.0000000000 ∙ 100 | 1.3409184604 ∙ 102 |
| 366 | 1.0000000000 ∙ 100 | 1.3372447112 ∙ 102 |
| 500 | 1.0000000000 ∙ 100 | 9.2587521977 ∙ 101 |
| 1000 | 1.0000000000 ∙ 100 | 2.3486162263 ∙ 101 |
| 2000 | 7.8388054837 ∙ 10−1 | 1.5112323776 ∙ 100 |
| 5000 | 4.0253613424 ∙ 10−4 | 4.0261395822 ∙ 10−4 |
| 10000 | 4.4410410772 ∙ 10−10 | 4.4410410781 ∙ 10−10 |

De grafiek van K1 (n) (de blauwe lijn)
en van K2 (n) (de rode lijn)

De grafiek van K1 (n) (de blauwe lijn)
en van K2 (n) (de rode lijn)
Voor hele grote waarden van n, zoals n = acht miljard, wordt de berekening van K1 nagenoeg ondoenlijk en zou mijn computer jaren rekentijd nodig hebben terwijl de berekening van K2 dan binnen een seconde is uitgevoerd. Voor lage waarden van n, ongeveer wanneer n < 5000, is de berekening van K2 veel te onnauwkeurig (en geeft zelfs uitkomsten groter dan één) en voldoet alleen de berekening van K1 (maar dat is dan ook binnen een paar minuten gefikst).
Dat allemaal ter harte nemend is de kans dat er op minstens één dag in het jaar niemand op Aarde jarig is, uitgaande van een jaar met 365 dagen en acht miljard mensen, dus:


 Door naar het volgende raadsel: een oneindig groot oppervlak verven
Door naar het volgende raadsel: een oneindig groot oppervlak verven Terug naar het vorige raadsel: vind de nulpunten van f (x) = ax − xa
Terug naar het vorige raadsel: vind de nulpunten van f (x) = ax − xa Overzichtspagina met raadsels
Overzichtspagina met raadsels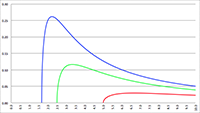 De integraal van
De integraal van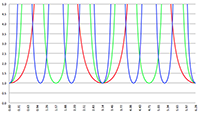 De integraal van
De integraal van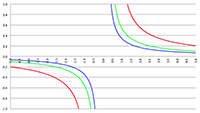 De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van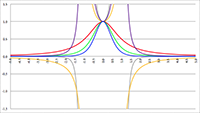 De integralen van
De integralen van Vectoren, vraagstuk 7
Vectoren, vraagstuk 7 Vectoren, vraagstuk 52
Vectoren, vraagstuk 52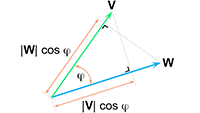 Invariantie van het inwendig product
Invariantie van het inwendig product Taylor-reeksen
Taylor-reeksen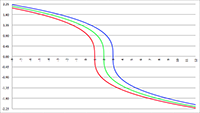 De Taylor-reeks van
De Taylor-reeks van Een reeks afsplitsen van
Een reeks afsplitsen van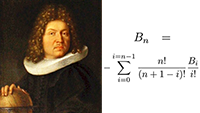 Bernoulli-getallen
Bernoulli-getallen Holomorfie van de functie
Holomorfie van de functie Relativiteitstheorie basic, hoofdstuk 3: het balletje
Relativiteitstheorie basic, hoofdstuk 3: het balletje Uitleg artikel precessie van Mercurius
Uitleg artikel precessie van Mercurius Het relativistische impulsmoment van een holle bol
Het relativistische impulsmoment van een holle bol Een lichtstraal bij een massa
Een lichtstraal bij een massa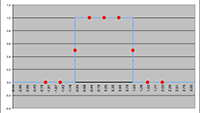 Fourier-analyse van het onzekerheidsprincipe van Heisenberg (I)
Fourier-analyse van het onzekerheidsprincipe van Heisenberg (I) Hoe ziet de wereld er morgen uit?
Hoe ziet de wereld er morgen uit? De illusie dat mijn geld mijn geld is
De illusie dat mijn geld mijn geld is De tweelingparadox
De tweelingparadox De energie van gravitatiestraling
De energie van gravitatiestraling Een dag zonder verjaardagen
Een dag zonder verjaardagen Het vermogen van gravitatiestraling
Het vermogen van gravitatiestraling Tijdsvertraging van een lichtstraal (2e orde benadering)
Tijdsvertraging van een lichtstraal (2e orde benadering) Tijdsvertraging van een lichtstraal (1e orde benadering)
Tijdsvertraging van een lichtstraal (1e orde benadering) Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein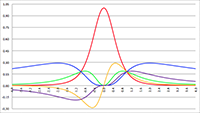 De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen