Differentiaal geometrie
Vaak wordt een functie beschreven als:
Maar om verschillende redenen kan het handig zijn, of zelfs noodzakelijk, om een
hulpvariabele of
parameter erbij te betrekken.
De functiebeschrijving wordt dan als volgt (in dit geval met gebruik van de parameter t):
In dergelijke gevallen zeggen we dat de functie gegeven is in
parametervorm.
Wanneer we doelbewust dit proces ingaan dan spreken we over het
parametriseren van een functie.
Dit is een voorbeeld van een functie in parametervorm:
Als je dit tekent dan krijg je een
astroïde:
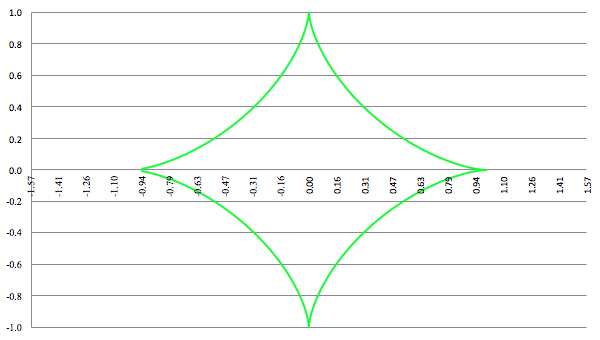
De grafiek van x (t) = cos
3 t, y (t) = sin
3 t
In dit voorbeeld is de parameter t op zich niet noodzakelijk, want we kunnen t uitdrukken als functie van x:
En dit kunnen we invullen in de functiebeschrijving van y:
Zo zijn we de parameter t kwijtgeraakt, maar geef toe dat deze laatste vergelijking er niet zo aantrekkelijk uitziet.
En er zijn genoeg gevallen waarbij het sterk gewenst is, of noodzakelijk is, om over te gaan op een functie
in parametervorm.
Een geparametriseerde functie is uiteraard ook te
differentiëren:
Het volgende onderwerp dat ik aan wil snijden is
booglengte.
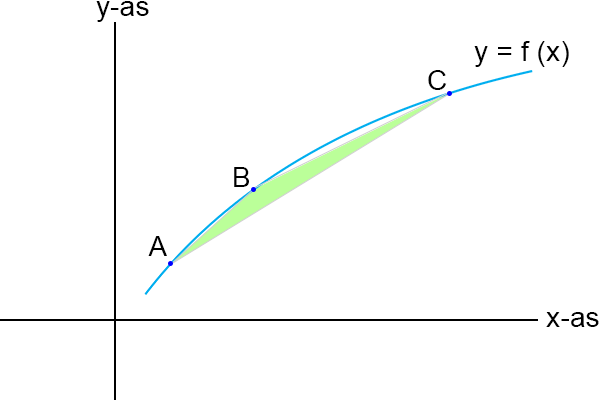
Stel, ik heb een bepaalde functie y = f (x) (waarvan ik hier maar een stukje getekend heb):
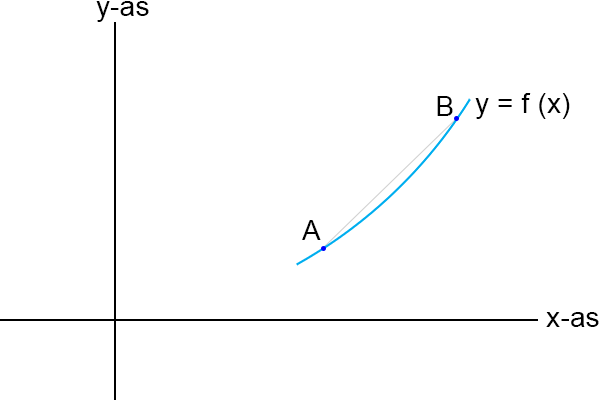
Ik kies vervolgens twee punten, A en B, die ik verbind middels een rechte lijn, een
koorde.
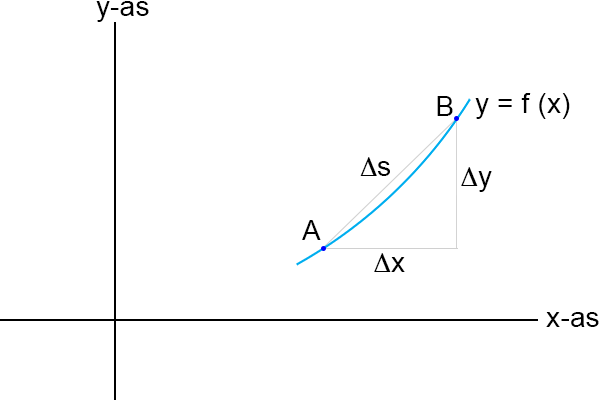
Laat ik ook even wat afstanden aangeven:
De horizontale afstand tussen A en B is ∆x, de verticale afstand tussen A en B is ∆y
en de lengte van de koorde is ∆s.
Dan geldt volgens de stelling van Pythagoras:
En als ik dan vervolgens ∆x en ∆y infinitesimaal klein laat worden ontstaat:
In dit geval dat dx en dy infinitesimaal klein zijn valt de koorde ds samen met de kromme en
is ds
de lengte van dat hele kleine stukje kromme.
De volgende stap is dan uiteraard om al die stukjes ds samen te nemen, door te
integreren, waaruit dan de
booglengte van de kromme ontstaat:
Voor een geparametriseerde functie is de afleiding als volgt:
Nu ga ik dit verhaal over booglengte knopen aan het verhaal over het parametriseren van functies.
Voor het parametriseren van een functie mag ik met een willekeurige parameter aan komen zetten.
Stel ik heb de volgende functie:
En vervolgens introduceer ik de parameter t:
Dit is niet echt bijzonder, maar ik kan ook het volgende doen:
Wanneer ik nu 1 eenheid t ‘verder ga’, dan komt dat overeen met 0.1 eenheid x (x = 10t, dus t = 0.1x).
Je zou kunnen zeggen dat ik kleinere stapjes geïntroduceerd heb, stapjes die 10 maal zo klein zijn.
En zo kan ik van alles bedenken om te gebruiken als parameter.
Ik zou ook de booglengte s als parameter kunnen gebruiken!
Hoe moet je je dat voorstellen?
Laten we eens uitgaan van de volgende functie, een parabool:
De
afgeleide hiervan is:
En daarmee wordt de booglengte:
Voor het oplossen van deze
integraal
heb ik gebruik gemaakt van de
tabel met integralen.
Nu kan ik voor iedere waarde van x de functiewaarde y (vergelijking (31)) en de booglengte s (vergelijking (33)) uitrekenen
en dat ziet er dan zo uit:
| x |
y |
s |
| 0.000 |
0.000 |
0.000 |
| 1.000 |
0.500 |
1.148 |
| 2.000 |
2.000 |
2.958 |
| 3.000 |
4.500 |
5.653 |
| 4.000 |
8.000 |
9.294 |
| 5.000 |
12.500 |
13.904 |
| 6.000 |
18.000 |
19.494 |
| 7.000 |
24.500 |
26.071 |
| 8.000 |
32.000 |
33.637 |
| 9.000 |
40.500 |
42.196 |
| 10.000 |
50.000 |
51.748 |
| Tabel 1 |
In de bovenstaande tabel bepaalt x eigenlijk het ‘marstempo’, maar ik kan dat natuurlijk ook door y laten bepalen
(y = 0.5x
2, dus x = √(2y)).
| x |
y |
s |
| 0.000 |
0.000 |
0.000 |
| 1.414 |
1.000 |
1.798 |
| 2.000 |
2.000 |
2.958 |
| 2.449 |
3.000 |
4.055 |
| 2.828 |
4.000 |
5.124 |
| 3.162 |
5.000 |
6.178 |
| 3.464 |
6.000 |
7.223 |
| 3.742 |
7.000 |
8.261 |
| 4.000 |
8.000 |
9.294 |
| 4.243 |
9.000 |
10.323 |
| 4.472 |
10.000 |
11.349 |
| Tabel 2 |
En de derde variant is uiteraard dat ik s gebruik als parameter:
| x |
y |
s |
| 0.000 |
0.000 |
0.000 |
| 0.893 |
0.398 |
1.000 |
| 1.528 |
1.167 |
2.000 |
| 2.019 |
2.038 |
3.000 |
| 2.429 |
2.950 |
4.000 |
| 2.787 |
3.883 |
5.000 |
| 3.108 |
4.830 |
6.000 |
| 3.402 |
5.786 |
7.000 |
| 3.674 |
6.748 |
8.000 |
| 3.928 |
7.715 |
9.000 |
| 4.168 |
8.686 |
10.000 |
| Tabel 3 |
Wanneer ik de booglengte s als parameter gebruik dan wordt de kromme zelf, in dit voorbeeld de parabool,
een soort flexibele as waar overal markeringsstreepjes staan telkens als ik 1 eenheid s verder ga.
Parametriseren met de booglengte is buitengewoon prettig, omdat dan de kromme zelf te beschouwen is
als een as: de s-as.
Hier zit nog wel een probleem, want vergelijking (33) geeft s als functie van x: s (x).
Maar wat ik eigenlijk wil weten is hoe x zich gedraagt als functie van s: x (s).
Kijk nog maar eens naar de vergelijkingen (2) en (3), daar staan x en y als functie van de parameter t.
Dus eigenlijk zou vergelijking (33) omgebouwd moeten worden zodat er geen s (x) staat, maar x (s).
Helaas, dat gaat mij niet lukken, en waarschijnlijk krijgt helemaal niemand dat voor elkaar.
Dus we zeggen wel heel gemakkelijk dat we een functie parametriseren met de booglengte, maar heel vaak
ontbreekt de exacte wiskundige beschrijving daarvoor.
En ergens is dat dan ook wel weer de charme van de wiskunde, want zolang we daar geen last van hebben
kunnen we gewoon doorgaan met waar we mee bezig zijn.
Het is net als praten over roze olifanten met drie slurfen, ze bestaan niet maar daarom hoeft dat een
goed gesprek niet in de weg te staan.
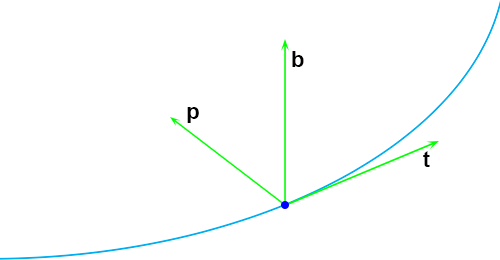
Indien ik een functie parametriseer met een willekeurige parameter t, dan vormen de
afgeleiden dx/dt en
dy/dt de componenten van de
raakvector r.
De lengte van deze raakvector is:
En toen ik hierboven de afleiding deed voor de booglengte van een geparametriseerde functie kwam het
volgende langs (vergelijking (23)):
Wanneer ik er voor kies om als parameter s te nemen (dus in plaats van t kies ik s) dan geldt voor
de raakvector:
En voor de booglengte:
Uit de combinatie van de vergelijkingen (35) en (37) volgt:
Voor een functie die geparametriseerd is met de booglengte is de raakvector altijd een eenheidsvector.
Deze eenheidsraakvector noem ik
t, en er geldt dus altijd |
t | = 1.
In zijn algemeenheid geldt voor iedere willekeurige functie
t =
r/|
r |.
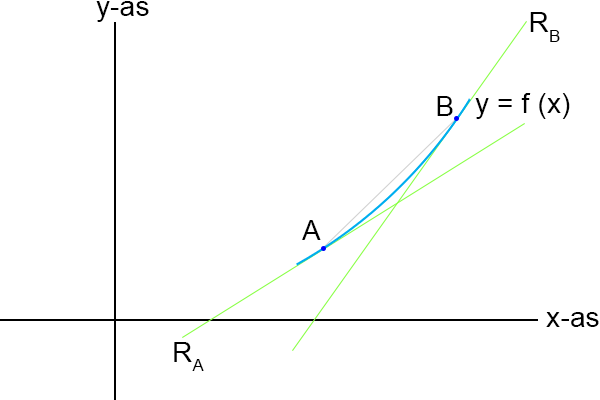
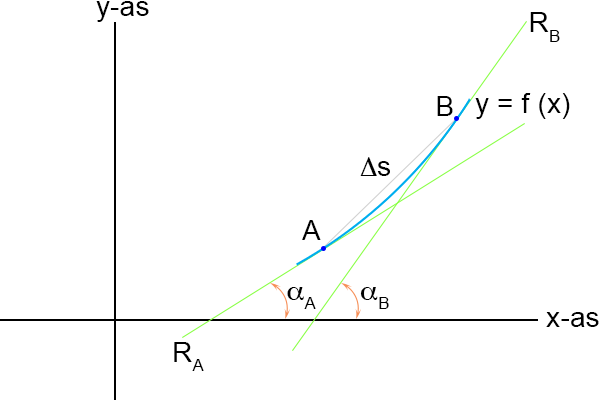
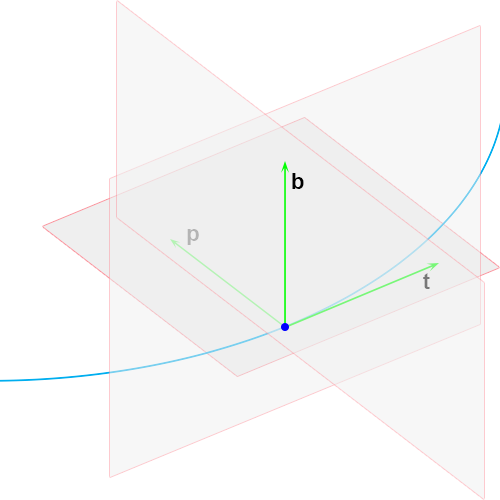
Laten we eens kijken naar het volgende plaatje:
De lijnen R
A en R
B zijn de raaklijnen in de punten A respectievelijk B.
Deze raaklijnen lopen niet evenwijdig aan elkaar, ze staan allebei onder een andere hoek.
Die hoeken noem ik α
A en α
B en die geef ik ook even aan in de grafiek.
Ik heb ook gelijk de lengte van de koorde, ∆s, aangegeven.
Het verschil tussen de hoeken α
A en α
B is een maat voor de
kromming van
de kromme.
Dit verschil noem ik ∆α en indien die nul zou zijn dan is het vrij simpel in te zien dat er geen
kromming is (wanneer ∆α = 0, dan valt de raaklijn in A samen met de raaklijn in B en is de kromme
een rechte lijn, en een rechte lijn is niet-krom, de kromming is nul).
Nu heb ik nog een zinvolle grootheid nodig om ∆α aan te relateren en dan is het het meest logische om
daar de kromme zelf voor te nemen, met andere woorden: door ∆α te relateren aan de booglengte ∆s.
Kromming geef ik aan met de letter κ.
Op deze manier hebben we de gemiddelde kromming over het stukje kromme van A naar B.
Indien we de kromming willen weten
in een bepaald punt (en dat willen we) dan zullen we ∆
infinitesimaal klein moeten maken:
De
tangens van α is gelijk aan dy/dx
(
overstaande zijde/
aanliggende zijde):
Waaruit volgt voor dα:
Let op: (dy/dx)
2 is de
afgeleide in het
kwadraat en d
2y/dx
2 is de
tweede afgeleide!
Hiervoor kwam tijdens de afleiding van de booglengte het volgende langs (vergelijking (17)):
Als ik dit allemaal samenvoeg (vergelijkingen (17), (40) en (43)) dan ontstaat een indrukwekkende vergelijking voor de kromming:
De reciproke waarde hiervan is de
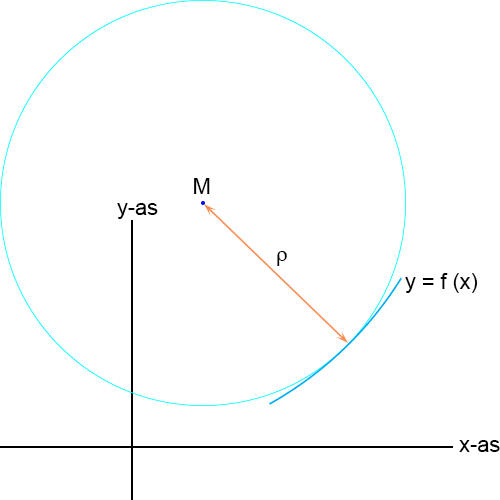
kromtestraal ρ:
Indien ik op een willekeurig punt van een kromme een cirkel tegen die kromme aanleg met een straal die gelijk is
aan de kromtestraal van de kromme in dat punt, dan komen de kromming van de cirkel en van de kromme in dat punt
met elkaar overeen.
Die denkbeeldige cirkel heet de
kromtecirkel of
raakcirkel of
osculatiecirkel
(osculation is het Engelse woord voor aanraking).
In een plaatje ziet dat er zo uit:
Het punt M heet het
kromtemiddelpunt.
Doorgaans zal ieder punt van een kromme een andere kromming hebben, dus ook een andere kromtestraal en dus ook
een ander kromtemiddelpunt.
Al die kromtemiddelpunten samen vormen uiteraard ook weer een kromme die we kunnen aangeven met m (x).
- De kromme m (x) is de evolute van f (x).
- De kromme f (x) is de involute of evolvente van m (x).
En hierbij wil ik ook nog even vermelden dat het de Nederlander Christiaan Huygens was die deze termen, evolute en involute, heeft geïntroduceerd.
Vergelijking (44) geeft de kromming van een functie y = f (x), maar hoe pakt dit nou uit voor een geparametriseerde functie?
Stel dat x = f (t) en y = g (t), de
afgeleide hiervan gaat volgens vergelijking (12):
Maar wat wordt dan de
tweede afgeleide?
Die vinden we met behulp van de
quotiëntregel:
De vergelijkingen (12) en (46) vullen we in in vergelijking (44):
Nu gaan we weer een stap verder door opnieuw een kromme te beschouwen en daar
drie punten op te kiezen,
A, B en C, en die verbind ik alledrie middels drie koordes.
Door deze drie punten A, B en C kan ik een vlak tekenen en dat vlak wil ik gaan beschrijven.
Dat is op zich simpel, ik neem
A als
steunvector en
AB en
AC allebei als
richtingsvector en klaar is Kees.
Maar ik wil uiteindelijk graag de beschrijving hebben van dit vlak
in het punt A.
Het is een (ingewikkelder) variant op het probleem van: hoe stel ik de vergelijking op van een raaklijn?
Indien ik de raaklijn in het punt A wil bepalen dan ga ik uit van het lijnstuk AB en vervolgens laat ik het
punt B naderen naar het punt A.
Maar nu gaat het niet om een raaklijn, maar om een
raakvlak.
Dat betekent logischerwijs dat ik zowel het punt B als het punt C naar het punt A moet laten naderen.
Om een raaklijn aan een kromme te definiëren heb ik een richtingsvector nodig en dat is dan de raakvector
aan de kromme.
Maar voor een raakvlak heb ik
twee richtingsvectoren nodig.
Een van die twee heb ik al, dat is de raakvector die ik verkrijg door het punt B naar A te laten naderen
en dan wordt de vector
AB de raakvector in het punt A.
Indien ik dit ook zou doen voor het punt C dan schiet ik daar niets mee op, want ik volg dan hetzelfde
procedé en dat levert nogmaals dezelfde raakvector op.
Dit soort situaties vraagt gewoon om gebruik van de trucendoos.
We gaan gebruik maken van de
reeksontwikkeling van Brook Taylor, een Engels wiskundige.
Daarbij geldt dat een functie te ontwikkelen is naar een polynoom, een functie met allemaal
machten van x,
door de functie telkens weer te differentiëren.
Dat ziet er dan als volgt uit (we ontwikkelen vanuit het startpunt x = a en we sommeren over n = 0, 1, 2, 3, 4, enzovoort):
Hierin is f
n de n
e
afgeleide van f (x).
Wil je wat voorbeelden zien?
Kijk dan in de
tabel met Taylor-reeksen.
We gaan uit van een functie die geparametriseerd is met een willekeurige parameter t en als startpunt kiezen we
uiteraard het punt A.
De vectoren
OA,
OB en
OC zijn
plaatsvectoren vanuit de oorsprong O.
Het punt B is ∆t
b verwijderd van het punt A en het punt C is ∆t
c verwijderd
van het punt A.
Nu kan ik de vectoren
OA,
OB en
OC als volgt beschrijven:
Hiermee ga ik de koordes
AB,
AC en
BC beschrijven:
Nu ga ik de vector
AB delen door ∆t
b.
Dan wordt de lengte van
AB weliswaar anders, maar hij ligt nog steeds in het vlak ABC.
Deze vector noem ik
AB*.
In het limietgeval dat ∆t
b naar nul nadert vallen alle termen met ∆t
b eruit en gaat
de vergelijking over in:
En dit is de ‘gewone’ raakvector aan de kromme, dus dit levert geen extra informatie op.
Voor de vector
AC kunnen we dit ook doen, maar dat zal dezelfde uitkomst opleveren.
Het zal daarom moeten gebeuren met de vector
BC.
Ik ga het
AB-deel van
BC delen door ∆t
b,
daarnaast ga ik het
AC-deel van
BC delen door ∆t
c
en bovendien ga ik alles vermenigvuldigen met 2.
Dit zijn allemaal getallen dus dat tast alleen de lengte van de vector aan en niet de richting.
Nu is het een goed moment om de haakjes weg te werken:
Vervolgens ga ik alles delen door (∆t
c − ∆t
b).
Dit zijn wederom allebei getallen dus dat tast alleen de lengte van de vector aan en niet de richting.
Tenslotte vervang ik (∆t
c + ∆t
b) door (∆t):
In het limietgeval dat ∆t
b en ∆t
c naar nul naderen vallen alle termen met ∆t
eruit en gaat de vergelijking over in:
Oftewel, de
tweede afgeleide!
De eerste richtingsvector die we zochten was de
eerste afgeleide
en de tweede richtingsvector is de
tweede afgeleide.
Verder wil ik even de
afgeleide
van het
inwendig product
van twee vectoren
V en
W doornemen:
Wanneer ik het
inwendig product
neem van een willekeurige vector met zichzelf ziet dat er zo uit:
Vergelijking (60) ga ik nu
differentiëren:
En als ik dan
V vervang door de raakvector d
A/dt:
Het
inwendig product
is alleen nul indien twee vectoren loodrecht op elkaar staan (of indien een van beide vectoren
de
nulvector is, de nulvector is een vector waarvan alle componenten nul zijn), oftewel de vectoren
d
A/dt en d
2A/dt
2 staan loodrecht op elkaar.
De raakvector aan de kromme,
de
eerste afgeleide dus, noem ik
r.
De vector d
2A/dt
2 staat hier loodrecht op en dus ook loodrecht op de kromme, deze
vector heet de
hoofdnormaal h.
Het raakvlak aan de kromme, waarin de raakvector en de hoofdnormaal liggen, heet het
osculatievlak.
Van de vectoren
h en
r kan ik eenheidsvectoren maken als volgt:
Ik noem vanaf nu de kromme
c (
vet gedrukt, dus
c is een vectorfunctie, ieder punt van
c is een plaatsvector vanuit de oorsprong naar een punt op de kromme), en
c is geparametriseerd
met een willekeurige parameter t, oftewel
c (t).
Wat weten we inmiddels?
De raakvector aan een kromme wordt gegeven door:
En de hoofdnormaal volgt uit:
Vergelijking (63) kan ik ook anders schrijven, waarbij ik vanaf nu nauwkeurig aangeef of ik te maken heb met de parameter s of met de
parameter t, dus of het
h (s) is of
h (t):
Ik neem aan beide zijden van vergelijking (67) het
uitwendig product met
t (s):
De vectoren
t en
p zijn eenheidsvectoren en staan loodrecht op elkaar, dus |
t ×
p | = 1:
De kromme
c (t) is in elk punt een vector met componenten x (t) en y (t).
Hieruit volgt voor het
uitwendig product
van de
eerste afgeleide met de
tweede afgeleide:
In combinatie met vergelijking (23) kan ik ook schrijven voor ds/dt:
En hier staat hetzelfde als vergelijking (47)!
Conclusie:
Vergelijking (63) is daarmee ook te schrijven als:
De normaalvector die loodrecht op het osculatievlak staat heet de
binormaal b en ontstaat uit het
uitwendig product
van de raakvector
t en de hoofdnormaal
p.
De vectoren
t en
p zijn beide eenheidsvectoren en staan loodrecht op elkaar, daardoor is
b per
definitie een eenheidsvector:
Ik kan me voorstellen dat het nu een beetje duizelt, dus tijd voor een overzicht:
Deze vectoren spannen een drietal vlakken op:
- De raakvector en de hoofdnormaal spannen het osculatievlak op.
De normaalvector van dit vlak is de binormaal.
Osculation (Engels) betekent aanraking.
- De hoofdnormaal en de binormaal spannen het normaalvlak op.
De normaalvector van dit vlak is de raakvector.
Het normaalvlak kun je zien als een soort kraagje van de kromme waar de kromme precies
loodrecht doorheen prikt.
- De binormaal en de raakvector spannen het rectifiërend vlak op.
De normaalvector van dit vlak is de hoofdnormaal.
Rectificeren betekent rechtzetten, in de elektronica heet een gelijkrichter in het
Engels rectifier.
De ruimte die door het drietal vectoren
b,
p en
t opgespannen wordt heet de
triëder.
Nu komt het allerergste: ik ga proberen het te tekenen.
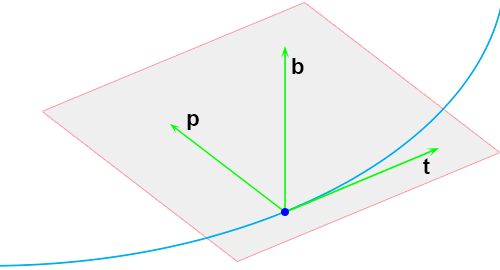
Allereerst het osculatievlak dat opgespannen wordt door
p en
t, de vector
b staat hier loodrecht op.
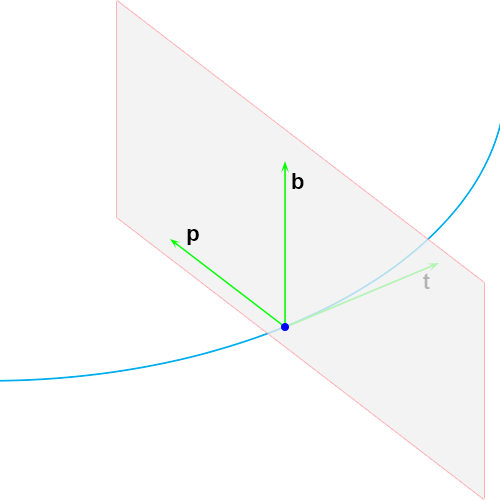
Vervolgens het normaalvlak dat opgespannen wordt door
b en
p, de vector
t staat hier loodrecht op.
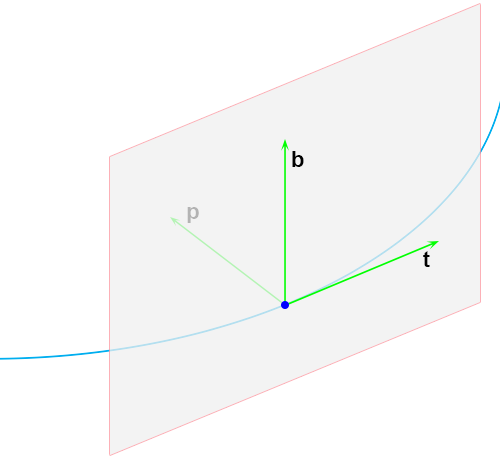
En tenslotte het rectifiërend vlak dat opgespannen wordt door
b en
t, de vector
p staat hier loodrecht op.
En voor de volledigheid alle vlakken samen:
Dat is inderdaad een grote puinhoop, maar het idee is overgekomen (hoop ik).
Ik laat ook een keer alle vlakken weg zodat alleen de triëder zichtbaar is:
De triëder is een
orthonormale vectorbasis (de basisvectoren staan allemaal loodrecht op elkaar
(= orthogonaal) én de basisvectoren zijn eenheidsvectoren) die in ieder punt van de kromme een andere
oriëntatie kan hebben.
Daarom wordt er ook vaak gesproken over de
bewegende triëder.
En daar gaan we op voortborduren, waarbij we vanaf nu uitgaan van een kromme die met de booglengte s is
geparametriseerd.
Stel, ik zit op het osculatievlak van de kromme en ik glij al zittend op dit vlak over de kromme.
Ik zie de raakvector
t recht vooruit wijzen (ik zit met mijn gezicht in de richting van de raakvector),
de hoofdnormaal
p wijst naar links en ik houd mij stevig vast aan de binormaal
b die loodrecht
op het osculatievlak staat.
De raakvector, de hoofdnormaal en de binormaal kun je zien als de assen waarom ik kan bewegen.
Wanneer ik draai om de hoofdnormaal-as dan ga ik omhoog of omlaag, oftewel er zit buiging (kromming) in de kromme.
Wanneer ik draai om de binormaal-as dan buig ik naar links of naar rechts, ook dit is buiging (kromming)
van de kromme.
Maar wanneer ik draai om de raakvector-as dan is het anders, want ik kan over een kaarsrechte kromme glijden
en toch draaien om de raakvector-as.
Dit is de draaiing die ik maak en loodrecht staat op mijn bewegingsrichting.
Deze draaiing noemen we
torsie en geven we aan met de letter τ.
Wanneer de binormaal ‘heen en weer’ gaat dan is er mogelijk torsie, dus torsie ontstaat door een d
b/ds.
En ik zeg mogelijk, want de d
b/ds die naar voren of naar achteren is gericht duidt op kromming en alleen
de d
b/ds die naar links of rechts is gericht geeft torsie aan.
Torsie is dus alleen de links-rechts gerichte component van d
b/ds, oftewel de projectie van
d
b/ds op de hoofdnormaal:
Omdat men torsie naar rechts als positief heeft gedefinieerd en de hoofdnormaal naar links wijst komt het
minteken in de vergelijking.
Gewoon een kwestie van afspraken.
De reciproke waarde van de torsie is de
torsiestraal σ:
Door vergelijking (61) weet ik dat een vector en zijn
afgeleide loodrecht op elkaar staan, dus
b en
d
b/ds staan loodrecht op elkaar.
Verder weet ik dat
b en
t loodrecht op elkaar staan en hun
inwendig product daarom nul is.
Daaruit kan ik het volgende afleiden:
Oftewel, d
b/ds staat zowel loodrecht op
b als op
t.
Hieruit volgt dat de vectoren
p en d
b/ds parallel lopen, waarbij d
b/ds het τ-de deel
is van
p (vergelijking (78)).
De afleiding volgens vergelijking (80) ga ik ook doen voor de vectoren
p en
t (die ook loodrecht op
elkaar staan):
En dit doen we dan ook nog maar even voor de vectoren
b en
p (die ook loodrecht op
elkaar staan):
Vergelijking (81) vertelt ons dat de projectie van d
p/ds op
t het −κ-de deel is van
t.
En vergelijking (82) vertelt ons dat de projectie van d
p/ds op
b het τ-de deel is van
b.
Verder weten we uit vergelijking (61) dat d
p/ds loodrecht op
p staat en dus in het rectifiërend vlak ligt.
Uit al deze wijsheid samen volgt:
Of via een andere weg:
Dit brengt ons bij een indrukwekkend trio vergelijkingen.
Uit vergelijking (73) volgt:
Uit de vergelijkingen (83) en (84) volgt:
En uit vergelijking (78) volgt:
Deze vergelijkingen zien er in matrixvorm nog mooier uit (en de punt boven de vectoren betekent
“
differentiëren naar s”):
Deze drie vergelijkingen zijn de geschiedenis ingegaan als de vergelijkingen van Frenet.
Maar ze worden ook vaak de vergelijkingen van Frenet-Serret genoemd.
En om niemand geweld aan te doen zouden ze eigenlijk de vergelijkingen van Frenet-Pagani-Serret genoemd moeten worden.
Deze drie mannen waren alledrie wiskundig (zeer) actief en hebben in de negentiende eeuw, onafhankelijk van elkaar,
de triëder van een willekeurige kromme ontdekt en beschreven.
Frenet staat in de geschiedenisboekjes, Serret staat in de kantlijn en Pagani ontbreekt.
Ik weet niet of het opgevallen is, maar ik begon dit wiskundehoofdstuk met de beschrijving van een kromme in twee
dimensies (vergelijkingen (1), (2), (3), enzovoort).
Maar gaandeweg ging ik steeds meer over vectoren praten waarvan de componenten geparametriseerd waren met t of s.
En toen maakte het eigenlijk helemaal niet meer uit of de kromme zich in een plat vlak (twee-dimensionaal) bevond
of vrij kronkelde in de ruimte (drie-dimensionaal).
Ik kan een twee-dimensionale kromme
c beschrijven als:
En
c is
vet gedrukt, want
c is een vectorfunctie.
De componenten van
c zijn x (t) en y (t).
De uitbreiding naar drie dimensies is simpel (en voor de hand liggend):
Ik kan x natuurlijk x
1 noemen, y noem ik dan x
2 en z is x
3.
Voor een willeurig aantal dimensies n geldt dan:
Dit verandert helemaal niets aan alles wat ik tot nu toe heb verteld.
Ook al slingert de kromme door een honderd-dimensionale ruimte dan verandert dat helemaal niets aan de
vergelijkingen die (bijvoorbeeld) de triëder beschrijven.
We gaan weer een stap verder.
Ik neem nogmaals vergelijking (90) erbij, maar in plaats van één parameter, t, beschrijf ik
c met twee
parameters: t
1 en t
2.
En later zal duidelijk worden waarom, maar ik heb goede redenen om de indices bij de parameters niet
laag maar hoog te schrijven.
Dus vanaf nu is het niet meer t
1 en t
2, maar t
1 en t
2.
Bovendien duid ik dit nieuwe ‘ding’ niet meer aan met
c maar met
v (en
v is
vet gedrukt want dit is ook een vectorfunctie):
Stel dat ik t
1 constant houd, t
1 is bijvoorbeeld 1, en t
2 laat ik variëren
van −∞ tot +∞, dan ontstaan er allemaal punten die uiteindelijk een bepaalde kromme vormen.
Wanneer ik vervolgens t
1 een beetje groter maak, bijvoorbeeld 1.001, en ik doorloop weer dezelfde
procedure dan vormt zich weer een kromme die (zeer waarschijnlijk) vlakbij de kromme ligt waar gold
t
1 = 1.
En zo kan ik dit ook doen voor t
1 = 1.002, t
1 = 1.003, t
1 = 1.004, enzovoort.
Uiteindelijk heb ik heel veel krommes die samen een vlak vormen.
Vergelijking (92) is de beschrijving van een vlak!
Ik heb het vlak
v visueel laten ontstaan door voor t
1 telkens een vaste waarde te nemen en
t
2 te variëren van −∞ tot +∞.
Op die manier ontstonden er allemaal krommes die samen het vlak vormden.
Met andere woorden, wanneer ik één parameter ‘vastzet’ dan heb ik de vergelijking van een kromme en die
kromme ligt in het vlak.
Dit kan ik op de volgende manieren doen, allereerst door één van beide parameters constant te maken
(a is een willekeurige constante, t is een willekeurige parameter):
Of door de parameters t
1 en t
2 ‘aan elkaar te knopen’ zodat ze niet meer onafhankelijk
van elkaar van −∞ tot +∞ kunnen gaan.
Dit is het geval indien de ene parameter een functie is van de ander of ze zijn allebei een functie van een
derde parameter:
Net als ik voorheen met de kromme heb gedaan kan ik nu ook het vlak
differentiëren.
En omdat er nu twee parameters zijn kan ik
differentiëren naar t
1 en t
2.
We moeten even afspreken hoe we dat gaan noteren.
De
eerste afgeleide naar t
1:
De
eerste afgeleide naar t
2:
De
tweede afgeleide naar t
1:
De
afgeleide
naar t
1 en naar t
2:
De
afgeleide
naar t
2 en naar t
1:
De
tweede afgeleide naar t
2:
Omdat het niet uitmaakt of ik eerst naar t
1 differentieer en daarna naar t
2 of andersom
volgt hieruit dat
v12 en
v21 gelijk zijn.
Wat verder nog heel interessant is om op te merken is dat
v1 en
v2
raakvectoren zijn aan het vlak
v.
En die twee raakvectoren kan ik gebruiken als de richtingsvectoren van een
raakvlak.
De beschrijving van het raakvlak
w in een punt P wordt dan (de plaatsvector
P van het punt P
gebruik ik als steunvector voor het raakvlak):
We kunnen het vlak ook
differentiëren
naar een willekeurige parameter t als volgt:
De vector d
v is een raakvector aan het vlak en is samengesteld uit de raakvectoren
v1 en
v2.
De lengte van de vector d
v is | d
v | en dat noem ik ds.
Nu ga ik het
inwendig product
nemen van de vector d
v met zichzelf.
Die
inwendige producten
leveren getallen op en daar ga ik ook namen voor bedenken:
Dit maakt ook duidelijk dat g
12 = g
21 en uiteindelijk ontstaat het volgende:
Vooral in wat oudere literatuur zie je ook wel staan:
Dit is de notatie zoals die gebruikt werd door Gauss, de grondlegger van de differentiaal geometrie.
Of nog anders opgeschreven, met indexnotatie (degenen die zich al verdiept hebben in de paragrafen over
relativiteitstheorie zullen dit zeker herkennen):
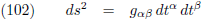
Deze uitdrukking heet de eerste fundamentele vorm (en of je het opschrijft als
vergelijking (100) of (101) of (102) mag je zelf weten, dat doet aan het principe niets af).
De componenten gαβ vormen samen de metrische tensor waarbij α
en β beide van 1 tot n lopen en n is het aantal dimensies van de ruimte (n = 1 voor een lijn,
n = 2 voor een vlak, enzovoort).
En nu valt ook alles op zijn plaats voor wat betreft de indices (hoog of laag).
De hoge indices staan voor contravariant en de lage indices voor covariant.
In de uitleg van paragraaf 5
van het artikel van Einstein over de algemene relativiteitstheorie
wordt alles precies uit de doeken
gedaan over coördinatentransformaties en wat de samenhang daarvan is met het covariant of contravariant
zijn van een vector (of in zijn algemeenheid: een tensor).
‘Gewone’ vectoren, zoals plaatsvectoren, steunvectoren en richtingsvectoren, zijn contravariant.
Voorbeelden van covariante vectoren zijn de basisvectoren van een vectorbasis en de
gradiëntvector van
een scalarveld.
En zoals je net hebt gezien is de metrische tensor ook covariant.
Wat je verder nog kunt zien aan de vergelijkingen (99b) en (99c) is dat de metrische tensor altijd symmetrisch is:
gαβ = gβα.
En aan de vergelijking (99a) en (99d) kun je aflezen wat de lengte van de vectoren v1 en
v2 is:
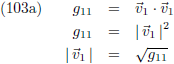
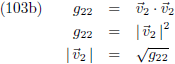
Wellicht is de vraag al opgekomen waarom je dit in het voortgezet onderwijs nooit hebt zien langskomen.
Dat komt omdat alle assenstelsels samengesteld waren uit assen die allemaal loodrecht op elkaar staan.
En alle coördinatenstelsels hadden mazen die allemaal even groot en vierkant zijn.
Dat de assen loodrecht op elkaar staan heet orthogonaal.
Een stelsel met orthogonale assen én regelmatige afstanden tussen de getallen heet Cartesisch
(naar de Franse wiskundige René Descartes).
De ruimte waar je dan over praat heet een Euclidische ruimte (vernoemd naar de Griek Euclides).
De metrische tensor van een Euclidische ruimte is heel simpel: een
hoofddiagonaal gevuld met enen
en verder allemaal nullen, oftewel de
eenheidsmatrix, en die kun je dus
net zo goed weglaten uit de vergelijkingen.
Het verschil tussen covariante vectoren en contravariante vectoren valt dan ook helemaal weg,
kortom het leven wordt buitengewoon eenvoudig.
In feite krijg je op school een zeer beperkte voorstelling van de werkelijkheid voorgeschoteld (en niet
alleen bij wiskunde, en niet alleen op school), die je vervolgens onbewust opneemt als de absolute waarheid.
Tijdens onze groei naar volwassenheid gebeurt dit talloze malen en indien we ons dat niet bewust worden
leven we de rest van ons leven binnen al die illusoire beperkingen.
Feitelijk leeft de overgrote meerderheid van de mensen daarom niet echt maar zijn we collectief aan het
‘slaapwandelen’ (zoals dat in spirituele teksten vaak genoemd wordt).
Maar binnen de algemene relativiteitstheorie
willen we absoluut van al die beperkingen af (in ieder geval van de wiskundige beperkingen ☺).
De assen van een assenstelsel hoeven niet loodrecht op elkaar te staan en de mazen van een coördinatenstelsel hoeven noch gelijk noch vierkant te zijn.
De ruimte waar je dan over praat heet een Riemann-ruimte (vernoemd naar Bernhard Riemann).
In een Riemann-ruimte ontkom je er niet aan om de metrische tensor aan boord te halen (en alles wat ik hier al besproken heb en nog ga bespreken).
De vectoren
v1 en
v2 zijn allebei raakvectoren aan het vlak
v
(vergelijkingen (95a) en (95b)).
Samen spannen ze het raakvlak
w op (vergelijking (96)).
Door het
uitwendig product
te nemen van de vectoren
v1 en
v2 ontstaat een
vector die loodrecht op het raakvlak staat, een normaalvector.
Van deze vector maak ik gelijk een eenheidsvector:
De noemer ga ik even apart uitwerken (φ is de hoek tussen de raakvectoren):
En dit stop ik weer in vergelijking (104a):
De vectoren
v1,
v2 en
n vormen samen een soort triëder
net zoals we eerder al gezien hebben bij de kromme.
Maar de triëder van de kromme bestaat uit drie eenheidsvectoren die allemaal loodrecht op elkaar
staan, terwijl
v1 en
v2 alleen eenheidsvectoren zijn als
g
11 respectievelijk g
22 gelijk aan één zijn (vergelijkingen (103a) en (103b)).
Bovendien staan
v1 en
v2 alleen loodrecht op elkaar indien
g
12 en g
21 nul zijn (vergelijkingen (99b) en (99c)).
Volgens vergelijking (89) kan ik een kromme beschrijven als volgt:
Deze kromme kan ik
differentiëren en dat ziet er dan zo uit:
Of iets anders opgeschreven:
Van deze vector ga ik het
inwendig product nemen met zichzelf:
Ik haal ook even vergelijking (24) terug in herinnering:
De vergelijkingen (24) en (107) ga ik combineren:
Ongemerkt doen we hier iets heel belangrijks.
De vergelijkingen (24) en (108) beschrijven allebei ds, maar vergelijking (24) is afgeleid van vergelijking (13) waarbij ik gebruik
heb gemaakt van de
stelling van Pythagoras.
Dat is op zich prima, maar dat mag alleen als ∆x en ∆y loodrecht op elkaar staan en voor
vergelijking (24) geldt dat dx/dt en dy/dt loodrecht op elkaar moeten staan.
Dus zonder het expliciet te vermelden ben ik uitgegaan van een Cartesisch coördinatenstelsel, maar
vergelijking (108) is uitgedrukt in vectoren.
Vectoren staan ‘los’ van coördinatenstelsels.
Hun componenten niet maar daar heeft vergelijking (108) geen boodschap aan.
Heel belangrijk om je dit te realiseren, vergelijking (108) geldt altijd, ongeacht het coördinatenstelsel en
ongeacht het aantal dimensies.
Wanneer ik overga van twee naar drie of vier of honderd dimensies dan moet ik vergelijking (24) herschrijven
terwijl er aan vergelijking (108) helemaal niets verandert.
Vergelijking (97) kan ik ook schrijven als:
De combinatie van de vergelijkingen (108) en (109) levert op:
De metrische tensor maakt het ons dus ook mogelijk om stukjes booglengte van een oppervlak te berekenen.
We gaan nog steeds uit van een willekeurig vlak
v volgens vergelijking (92).
En door (of over?) dat vlak kronkelt een willekeurige kromme
c.
Vervolgens beschouwen we een punt Ж ergens op de kromme en dus ook ergens op het vlak.
In het punt Ж is uiteraard de triëder aanwezig met de eenheidsvectoren
t,
p en
b
die allemaal onderling loodrecht op elkaar staan.
En in het punt Ж is er uiteraard ook een normaalvector
n die loodrecht op het vlak staat.
We weten inmiddels dat de vector
p in de richting wijst waar de kromme heenbuigt.
En we weten ook dat de vectoren
n en
p allebei in het normaalvlak van de kromme liggen.
Het normaalvlak is een soort kraagje om de kromme dat opgespannen wordt door de hoofdnormaal
p en
de binormaal
b.
In het willekeurige punt Ж staat de normaalvector
n loodrecht op het vlak
v en daardoor
ook loodrecht op de kromme
c die door het punt Ж kronkelt, dus
n ligt in het normaalvlak.
Allereerst nemen we nu het
inwendig product
van de eenheidsvectoren
p en
n (φ is de hoek tussen de vectoren):
Indien we een punt Ж beschouwen op een vlak dat ook ‘echt vlak is’, bijvoorbeeld de tafel waaraan je
nu zit te werken, dan steekt de normaalvector
n recht omhoog.
Hoe de kromme door het punt Ж kronkelt maakt dan helemaal niets uit, want de vector
p ligt
dan altijd in het vlak en de hoek φ is dan altijd 90° en cos φ = 0.
Uit vergelijking (66) weten we dat
h de
tweede afgeleide
is van de kromme en vergelijking (73) vertelt ons hoe we
daar de eenheidsvector
p van hebben gemaakt.
Daarmee kunnen we vergelijking (112) ook schrijven als:
In lijn met de notatie van de vergelijkingen (95c/d/e/f) kan ik de
tweede afgeleide van het vlak schrijven als:
En dit kan ik net zoals in vergelijking (97) omschrijven in het geval dat we
differentiëren naar een willekeurige parameter t:
Vervolgens nemen we aan beide zijden het
inwendig product
met de normaalvector
n:
Nu introduceer ik een nieuw ‘ding’ genaamd b:
Dit nieuwe ‘ding’ b bestaat uit de
tweede afgeleide
van het vlak (
vαβ) en
de normaalvector van het vlak (
n), oftewel b wordt volledig bepaald door het vlak en is
onafhankelijk van de kromme die over het vlak kronkelt.
Ik kan nu het rechterlid van vergelijking (116) schrijven als:
Deze uitdrukking noemen we de
tweede fundamentele vorm.
In wat oudere literatuur zie je ook wel staan:
Tenslotte pakken we de vergelijkingen (113), (116) en (117) samen:
In vergelijking (115) heb ik gedifferentieerd naar een willekeurige parameter t, maar ik kan natuurlijk ook
differentiëren naar de parameter s (de booglengte).
Vergelijking (120) gaat dan over in:
En ik introduceer de
normale kromming κ
n:
Zodat we na al dit geknutsel het volgende resultaat hebben:
De teller van deze vergelijking, b
αβ dt
α dt
β, wordt
volledig bepaald door het vlak en de noemer van deze vergelijking,
g
αβ dt
α dt
β, wordt volledig bepaald door de
kromme die over het vlak kronkelt.
De raaklijnen
vα van het vlak
v (zie vergelijkingen (95a) en (95b)) staan uiteraard
loodrecht op de normaalvector
n van het vlak.
Er geldt dus:
Door vergelijking (124) te
differentiëren ontstaat:
Met gebruikmaking van vergelijking (117) kan ik ook schrijven:
Aldus geldt volgens de vergelijkingen (98) en (102):
En volgens de vergelijkingen (116), (118) en (126) geldt:
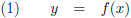
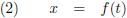
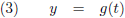
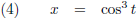
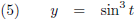

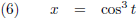
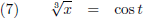
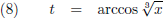
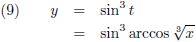
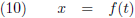
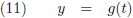
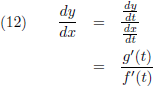
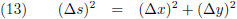
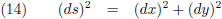
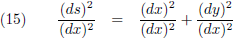
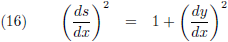
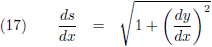
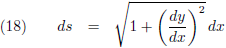
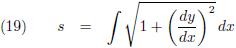
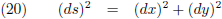
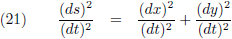
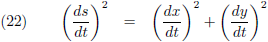
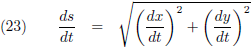
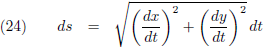
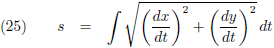
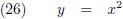
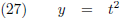
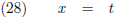
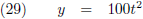
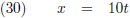
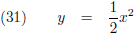
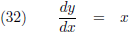
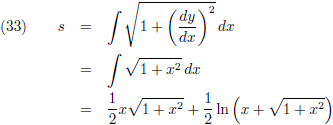
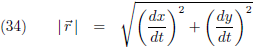
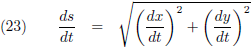
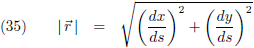
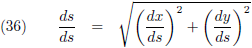
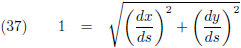
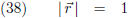
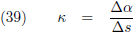
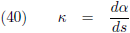
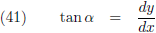
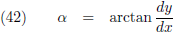
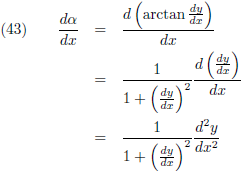
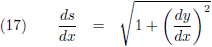
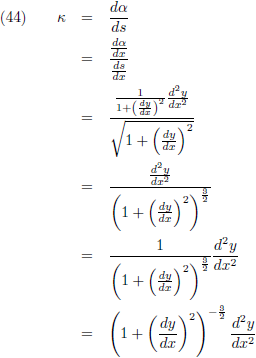
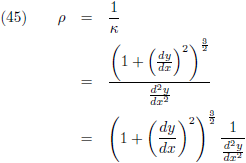
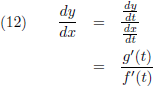
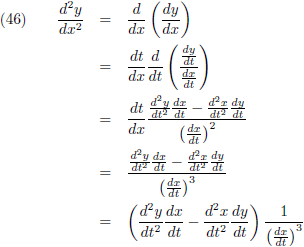
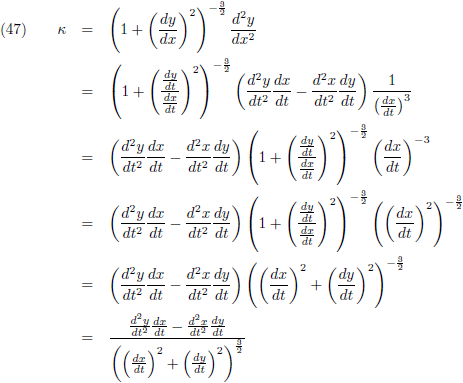
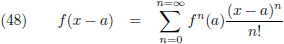
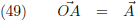
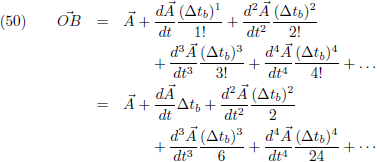
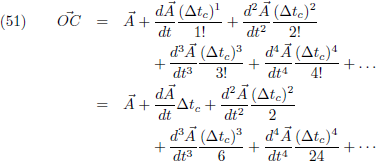
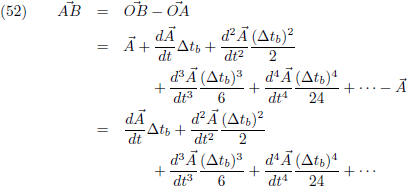
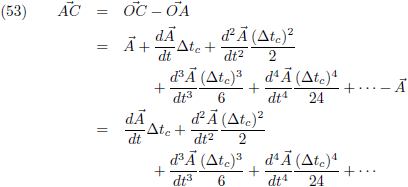
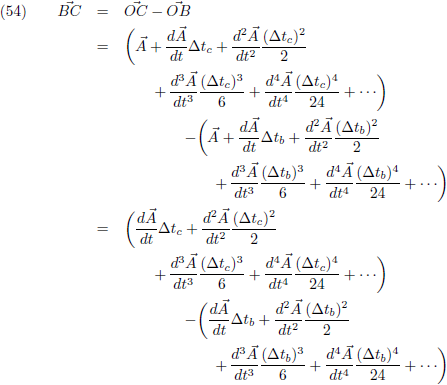
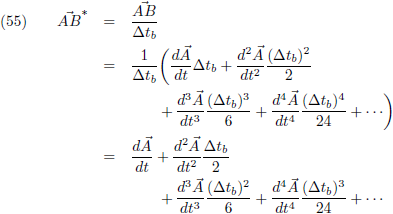
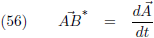
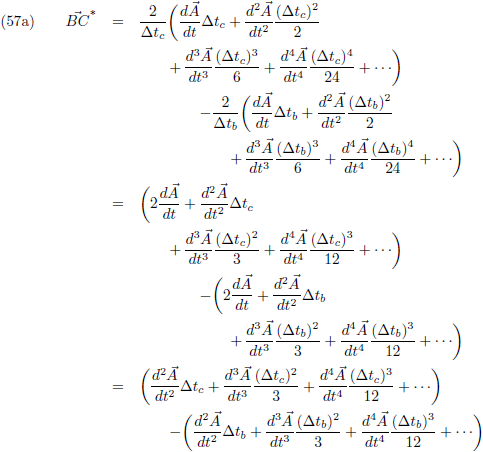
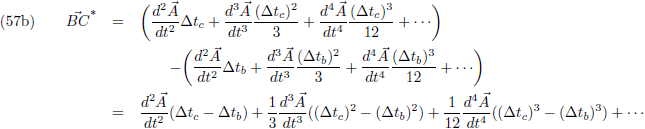
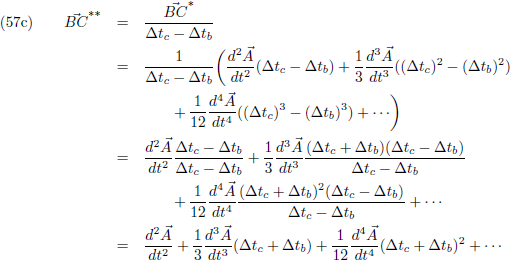
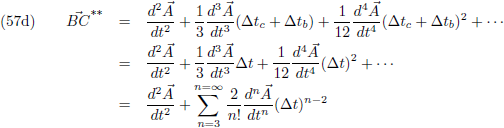
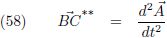
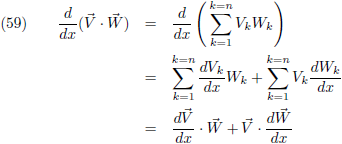
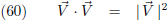
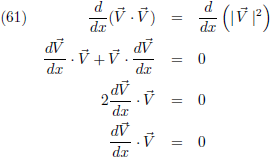
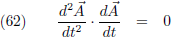
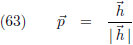
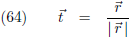
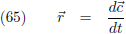
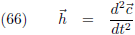
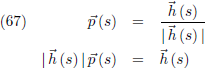
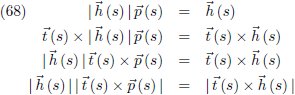
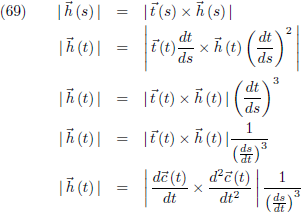
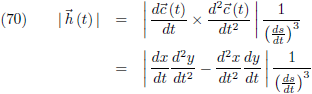
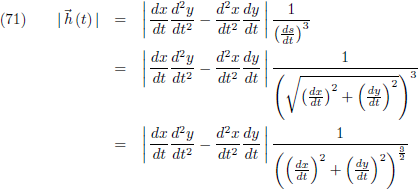
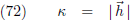
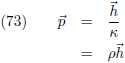
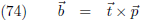
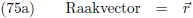
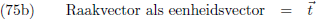
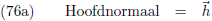
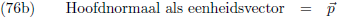
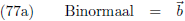
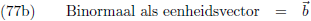
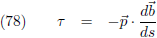
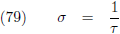
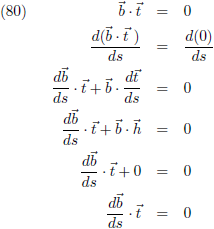
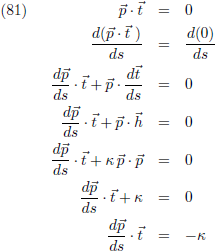
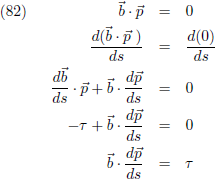
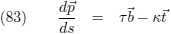
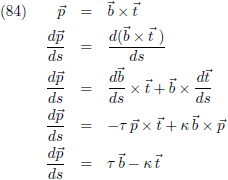
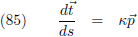
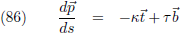
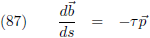
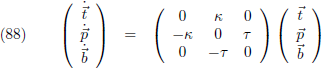
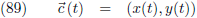
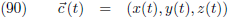
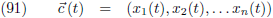
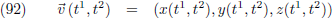
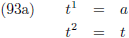
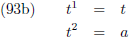
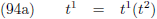
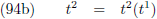
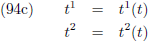
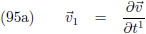
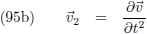
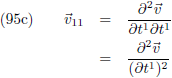
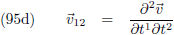
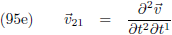
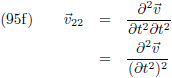
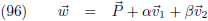
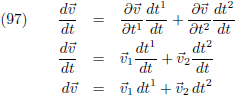
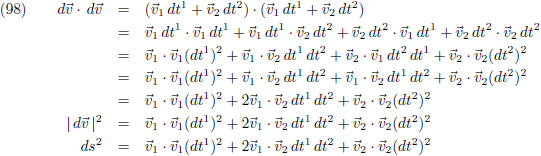
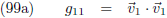
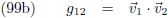
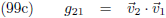

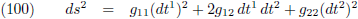
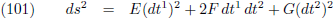
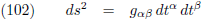
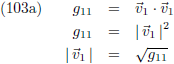
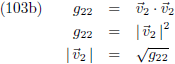
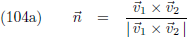

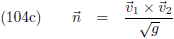
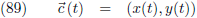
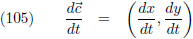
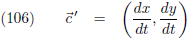
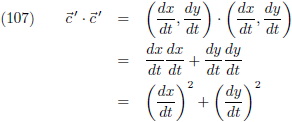
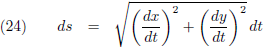
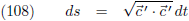
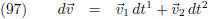
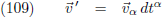
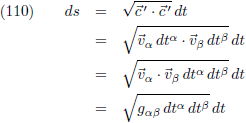
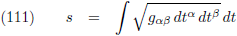
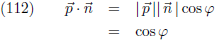
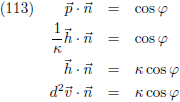
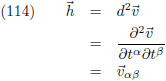
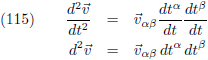
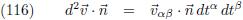
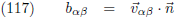
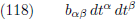
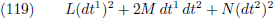
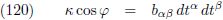
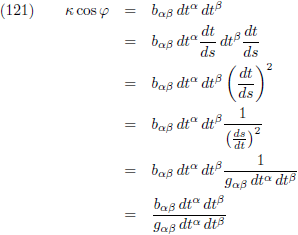

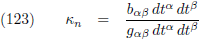
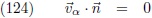
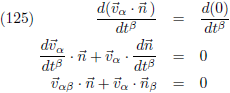
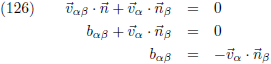
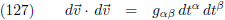
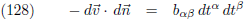










 De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 21
Vectoren, vraagstuk 21 Vectoren, vraagstuk 59
Vectoren, vraagstuk 59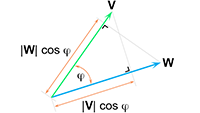 Invariantie van het inwendig product
Invariantie van het inwendig product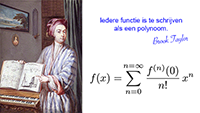 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 4: de zaklamp
Relativiteitstheorie basic, hoofdstuk 4: de zaklamp Uitleg artikel algemene relativiteitstheorie: inleiding hoofdstuk D
Uitleg artikel algemene relativiteitstheorie: inleiding hoofdstuk D Wat is geodetisch?
Wat is geodetisch? De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt Kwantummechanica
Kwantummechanica Afleiding van de algemene golfvergelijking
Afleiding van de algemene golfvergelijking De illusie van ons onderwijssysteem
De illusie van ons onderwijssysteem De reis naar de werkelijkheid van Anky van Grunsven
De reis naar de werkelijkheid van Anky van Grunsven De djembé
De djembé De Natuur spreekt: The Soil/De Grond
De Natuur spreekt: The Soil/De Grond Natuurkundeclub Gℏc
Natuurkundeclub Gℏc LaTeX code
LaTeX code Kalender van de jaren 0181 − 0190 met weekdagen
Kalender van de jaren 0181 − 0190 met weekdagen Kalender van de jaren 0561 − 0570 met weekdagen
Kalender van de jaren 0561 − 0570 met weekdagen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen