Het vermogen van gravitatiestraling
Bereken het vermogen dat twee hemellichamen, die om elkaar heen draaien in een elliptische baan,
genereren aan gravitatiestraling.
Ga ervanuit dat het zwaartekrachtveld zwak is en dat de snelheden niet-relativistisch zijn
(v

c).
Zoals een speedboot golven veroorzaakt in het water, zie het plaatje hieronder, zo is het ook met
objecten die zich bewegen door de ruimtetijd, zij veroorzaken golven in de ruimtetijd.

Een speedboot veroorzaakt golven in het water
Omdat de ruimtetijd een ‘starre constructie’ is zijn golven in de ruimtetijd, zwaartekrachtgolven, minimaal.
Zelfs een groot object als een planeet genereert zwaartekrachtgolven met een totaal onmeetbare amplitude.

Een planeet veroorzaakt golven in de ruimtetijd
Omdat het betreffende object door de ruimtetijd ‘ploegt’ kost dat vermogen.
Hoeveel?
Dat ga ik op deze pagina uitrekenen voor twee hemellichamen die om elkaar heen draaien in een elliptische baan.
De oorsprong van het assenstelsel plaats ik in (het zwaartepunt van) één der beide hemellichamen, dus
één hemellichaam ‘beweegt niet’.
Daarnaast is het belangrijk om de notatie duidelijk te maken, zodat daar geen verwarring over kan ontstaan.
De afstand tussen (de zwaartepunten van) beide hemellichamen is
r, een
vector met de volgende componenten:
De snelheid is de
afgeleide hiervan,
respectievelijk als
vector, in
componenten en radieel (gericht langs r, daarom de index r):
De kracht die beide hemellichamen op elkaar uitoefenen is uiteraard gericht langs r, en uit de eerste
wet van Newton volgt dat geldt voor de versnelling:
Omdat m een scalaire grootheid is, een getal, volgt hieruit dat de versnelling ook gericht is langs r.
De versnelling is de
afgeleide van de
snelheid, wederom als
vector, in
componenten en radieel (gericht langs r, daarom de index r):
Voor dit probleem hebben we ook nog de
schok [Engels:
jerk, vandaar de letter j] nodig, de
afgeleide van de
versnelling, nogmaals als
vector, in
componenten en radieel (gericht langs r, daarom de index r):
Omdat het zwaartekrachtveld zwak is én omdat de snelheden niet-relativistisch zijn mag ik Newtonse
hemelmechanica gebruiken.
Daarom haal ik even wat vergelijkingen op van de pagina
hemelmechanica, om te beginnen de totale massa
(vergelijking (21a) op die pagina):
De afstand r (vergelijking (58) op de pagina
hemelmechanica):
De snelheid v (vergelijking (63) op de pagina
hemelmechanica):
De radiële snelheid v
r (vergelijking (65) op de pagina
hemelmechanica):
Verder definieer ik de
gereduceerde massa:
Ik gebruik uiteraard de gravitatiewet van Newton:
Hieruit volgt voor de versnelling:
Of als
vector geschreven (het dakje boven de r
betekent dat het een
eenheidsvector is):
Door de versnelling te
differentiëren naar de tijd
vind ik de schok:
En om voorbereid te zijn op wat komen gaat ga ik een aantal
inwendige producten uitrekenen:
De volgende stap is om het
traagheidsmoment
uit te rekenen, de wiskundige definitie van het
traagheidsmoment is:
Omdat het hier gaat om twee hemellichamen, die ik voorstel als puntmassa’s, wordt het
traagheidsmoment:
Dit moet ik driemaal
differentiëren naar t
(de tijd, weldra zal duidelijk worden waarom).
De
eerste afgeleide is:
De
tweede afgeleide is:
En de derde
afgeleide is:
Met behulp van de vergelijkingen (2), (4) en (5) wordt dit:
Vervolgens ga ik
kwadrateren:
Nu ga ik sommeren over de indices:
Dit gaan we even in stukken hakken, ik begin met de eerste term tussen de haakjes:
Vervolgens de tweede term:
En tenslotte de derde term:
Vervolgens stop ik dit alles in vergelijking (23):
Het
spoor [Engels:
trace, de som van de
componenten op de
hoofddiagonaal]
van het
traagheidsmoment (in tensorvorm) is:
Ook dit moet ik driemaal
differentiëren naar t.
De
eerste afgeleide is:
De
tweede afgeleide is:
En de derde
afgeleide is:
Met behulp van de vergelijkingen (2), (4) en (5) wordt dit:
Vervolgens ga ik weer
kwadrateren:
Dan kunnen we nu echt beginnen aan het oorspronkelijke probleem.
Het gravitatiestralingvermogen dat de beide hemellichamen genereren volgt uit de
massaquadrupoolvergelijking [Engels:
mass quadrupole equation, dat zijn drie woorden,
maar in correct Nederlands moet het aan elkaar]:
Q is de
quadrupooltensor en de hoge index T betekent dat het spoor van de tensor
niet meegenomen dient te worden [Engels:
trace-free of
traceless].
In meer detail ziet de massaquadrupoolvergelijking er als volgt uit:
Al het voorwerk is al verricht, dus ik kan de vergelijkingen (25) en (31) direct invullen:
Nu ga ik de
inwendige producten,
de vergelijkingen (15), inzetten om orde te scheppen in deze chaos:
Kijk, dat ziet er een stuk netter uit.
Merk ook op dat de schok er helemaal niet meer in voorkomt.
Dan komt nu het moment om
baanelementen
in te brengen:
Met behulp van de vergelijkingen (8), (9) en (12) wordt vergelijking (35):
Vervolgens ga ik r omschrijven middels vergelijking (7) en krijg ik het vermogen als functie van de hoek θ:
De eerste term aan de rechterkant bevat alleen maar constanten, en daarom is het wel zinvol om de overige termen
even onder te brengen in een aparte functie:

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.001 oplopend tot e = 0.01 (de lichtblauwe lijn)

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.01 oplopend tot e = 0.1 (de lichtblauwe lijn)

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.1 oplopend tot e = 0.99 (de lichtblauwe lijn)
De grafieken laten duidelijk zien dat:
- het vermogen constant is voor een cirkelvormige baan (e = 0, de rode lijn in bovenstaande grafieken),
- het vermogen maximaal is voor θ = 0 = 2π, dus tijdens de passage van het
periapsis waar de snelheid het hoogst is,
- het vermogen minimaal is voor θ = π, dus tijdens de passage van het
apoapsis waar de snelheid het laagst is,
- het vermogen zeer sterk toeneemt wanneer de
excentriciteit van de baan toeneemt.

De grafiek van f (e, θ) voor θ = 0

De grafiek van f (e, θ) voor θ = 0,
logaritmische verticale schaalverdeling

De grafiek van f (e, θ) voor θ = π
Ik kijk nog even naar de passage van het
periapsis.
Daar is de hoek θ nul en dan wordt het vermogen maximaal:
De energie die dan in één seconde weggestraald wordt is:
Volgens Einstein’s beroemde formule
is energie equivalent aan massa:
Gecombineerd met vergelijking (40) wordt dit:
Ik raadpleeg de
tabel met fysische gegevens:
| Gravitatieconstante |
G |
6.67428 ∙ 10−11 |
m3/(kg s2) |
| Lichtsnelheid |
c |
(exact) 2.99792458 ∙ 108 |
m/s |

ZON |
| Massa |
m |
1.9891 ∙ 1030 |
kg |

AARDE |
| Halve lange baanas |
a |
7.60487985 ∙ 1010 |
m |
| Excentriciteit van de baan |
e |
0.0167086 |
|
| Massa |
m |
5.9742 ∙ 1024 |
kg |
Waarna een rekenmachine mij vertelt dat wanneer de Aarde door het
perihelium gaat er per seconde 6.4 kJ
aan energie uitgestraald wordt en dat de Aarde daardoor per seconde ruim 70 picogram massa verliest.
 c).
c).
 c).
c).





































































 Door naar het volgende vraagstuk: de energie van gravitatiestraling
Door naar het volgende vraagstuk: de energie van gravitatiestraling Terug naar het vorige vraagstuk: tijdsvertraging van een lichtstraal, 2e orde benadering
Terug naar het vorige vraagstuk: tijdsvertraging van een lichtstraal, 2e orde benadering Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie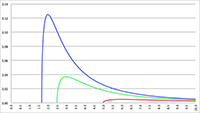 De integraal van
De integraal van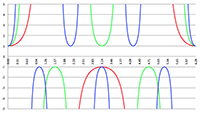 De integraal van
De integraal van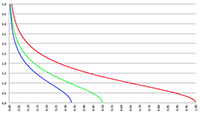 De integraal van
De integraal van De integraal van
De integraal van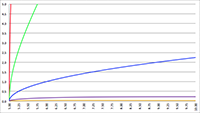 De integralen van
De integralen van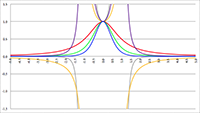 De integralen van
De integralen van Vectoren, vraagstuk 6
Vectoren, vraagstuk 6 Vectoren, vraagstuk 51
Vectoren, vraagstuk 51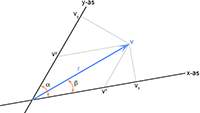 Covariante - en contravariante componenten van een vector
Covariante - en contravariante componenten van een vector Taylor-reeksen
Taylor-reeksen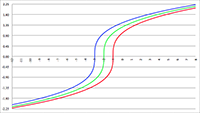 De Taylor-reeks van
De Taylor-reeks van Een reeks afsplitsen van
Een reeks afsplitsen van Faculteiten
Faculteiten Holomorfie van de functie
Holomorfie van de functie Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid
Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie
Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie De relativistische rotatie-energie van een massieve bol
De relativistische rotatie-energie van een massieve bol Een botsing met een zandkorrel
Een botsing met een zandkorrel Een analogie van het onzekerheidsprincipe van Heisenberg
Een analogie van het onzekerheidsprincipe van Heisenberg Terugkijkend vanaf je sterfbed, wat ga je NU doen?
Terugkijkend vanaf je sterfbed, wat ga je NU doen? De tweelingparadox
De tweelingparadox Een dag zonder verjaardagen
Een dag zonder verjaardagen Het vermogen van gravitatiestraling
Het vermogen van gravitatiestraling Tijdsvertraging van een lichtstraal (1e orde benadering)
Tijdsvertraging van een lichtstraal (1e orde benadering) Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein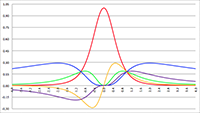 De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen