De massa van de atmosfeer
Bereken de massa van de atmosfeer van de Aarde.
De Aarde wordt omgeven door allerlei gassen die we samen de atmosfeer noemen.
Deze atmosfeer maakt het leven hier op Aarde mogelijk, want de atmosfeer voedt ons en beschermt ons.
De zwaartekracht die de Aarde genereert zorgt dat de atmosfeer bij de Aarde blijft en niet vervliegt
in de ruimte (waarbij de temperatuur ook een rol speelt, want hoe hoger de temperatuur hoe gemakkelijker
de atmosfeer ‘er vandoor gaat’).

Zonder atmosfeer zouden we niet dit soort
spectaculaire zonsondergangen hebben

De Maan heeft geen atmosfeer, omdat de Maan onvoldoende
zwaartekracht genereert om een atmosfeer te behouden

De dwergplaneet Pluto heeft nog minder zwaartekracht
dan de Maan, maar door de zeer lage temperatuur
is er toch een (zeer ijle) atmosfeer
(Credits: NASA)

De planeet Saturnus heeft geen vast oppervlak en
bestaat feitelijk alleen uit atmosfeer
(Credits: NASA)
De vraag waar het hier om gaat is wat de massa is van de aardse atmosfeer.
Stel dat we omringd worden door meetinstrumenten en een rekenmachine, kunnen we dan
ter plekke
de massa van de totale atmosfeer bepalen?
Ja, dat kan.
De definitie van dichtheid is massa gedeeld door het volume van die massa:
Of iets anders opgeschreven:
Ik neem links en rechts de
differentiaal:
Het infinitesimale volume dV is het boloppervlak maal een infinitesimaal afstandje dr:
Vervolgens ga ik links en rechts
integreren
(r
A is de straal van de Aarde):
De dichtheid van de atmosfeer neemt uiteraard af met de hoogte, en omdat alle natuurlijke processen als
e-
macht verlopen geldt
dat ook hier.
Met de index “0” geef ik telkens het aardoppervlak aan en τ is een nog te bepalen constante:
Dit vul ik in in vergelijking (5):
Deze
integraal zoek ik op in de
tabel met integralen:
Hiermee wordt vergelijking (7):
Omdat τ veel kleiner zal zijn dan r
A mag ik dit vereenvoudigen tot:
Nu moet ik de constante τ nog bepalen.
Voor de luchtdruk aan het aardoppervlak geldt:
g is de valversnelling als gevolg van de zwaartekracht en die volgt uit de gravitatiewet van Newton:
De vergelijkingen (7) en (12) vul ik in in vergelijking (11) en die ga ik vervolgens uitwerken:
Oftewel:
Waarmee vergelijking (10) tenslotte wordt:
Vervolgens gebruik ik mijn meetinstrumenten (of ik raadpleeg de
tabel met fysische gegevens) en vind ik:
| Gravitatieconstante |
G |
6.67428 ∙ 10−11 |
m3/(kg s2) |
| Luchtdruk |
p0 |
1.01325 ∙ 105 |
kg/(m s2) |
| Massa van de Aarde |
MA |
5.9742 ∙ 1024 |
kg |
Straal van de Aarde
(bij de evenaar) |
rA |
6.378137 ∙ 106 |
m |
Waarna een rekenmachine mij vertelt:
Deze waarde ligt maar 2.7% (!) boven de waarde die
Wikipedia geeft
(5.1480 ∙ 10
18 kg), terwijl ik helemaal geen rekening houd met het feit dat de Aarde niet
vlak is, dat de Aarde niet homogeen is, dat de Aarde niet perfect bolvormig is en zo zijn er nog wel wat
dingetjes op te noemen.





















 Door naar het volgende vraagstuk: afleiding van de algemene golfvergelijking
Door naar het volgende vraagstuk: afleiding van de algemene golfvergelijking Terug naar het vorige vraagstuk: de opwarming van de Aarde
Terug naar het vorige vraagstuk: de opwarming van de Aarde Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van De integralen van
De integralen van Vectoren, vraagstuk 20
Vectoren, vraagstuk 20 Vectoren, vraagstuk 65
Vectoren, vraagstuk 65 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT De Taylor-reeks van
De Taylor-reeks van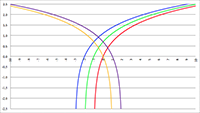 De Taylor-reeksen van
De Taylor-reeksen van Bijzondere figuren
Bijzondere figuren Holomorfie van de functie
Holomorfie van de functie Samenvatting van de holomorfietabel van complexe functies
Samenvatting van de holomorfietabel van complexe functies Uitleg artikel algemene relativiteitstheorie: paragraaf 18
Uitleg artikel algemene relativiteitstheorie: paragraaf 18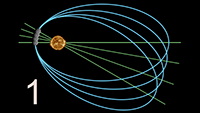 Relativistische periheliumprecessie, 1e orde benadering
Relativistische periheliumprecessie, 1e orde benadering De oppervlaktezwaartekracht van een zwart gat
De oppervlaktezwaartekracht van een zwart gat Elektriciteit en magnetisme
Elektriciteit en magnetisme Wanneer heb je voor het laatst iets nieuws gedaan?
Wanneer heb je voor het laatst iets nieuws gedaan? De illusie dat ik onmisbaar ben
De illusie dat ik onmisbaar ben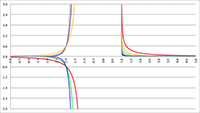 De integralen van
De integralen van De integralen van
De integralen van De integralen van
De integralen van De massa van de atmosfeer
De massa van de atmosfeer Hyper-Catalan-getallen
Hyper-Catalan-getallen Een ontmoeting met aliens
Een ontmoeting met aliens Ze durven niet
Ze durven niet Fuss-getallen
Fuss-getallen Ze mogen niet
Ze mogen niet Catalan-getallen
Catalan-getallen Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen