De energie van gravitatiestraling
Bereken de energie die twee hemellichamen, die om elkaar heen draaien in een elliptische baan,
genereren aan gravitatiestraling:
- als functie van de hoek,
- en gemiddeld per omloop.
Ga ervanuit dat het zwaartekrachtveld zwak is en dat de snelheden niet-relativistisch zijn
(v

c).
Een druppel veroorzaakt golven (golfjes) wanneer die in het water valt, zie het plaatje hieronder.

Een druppel veroorzaakt golven in het water
wanneer die in het water valt
Zo is het ook met objecten die zich bewegen door de ruimtetijd, zij veroorzaken golven in de ruimtetijd.
Een hemellichaam dat valt in de ruimtetijd of als een jojo op en neer gaat veroorzaakt golven (nou niet
erover nadenken
hoe je een hemellichaam laat vallen of als een jojo op en neer laat gaan, dat
doet even niet ter zake).

Een hemellichaam veroorzaakt golven in de ruimtetijd
wanneer die in de ruimte ‘valt’ of op en neer gaat
Middels de gravitatiestraling (zwaartekrachtgolven) wordt er energie weggevoerd uit het systeem.
Op
deze pagina heb ik het vermogen van die
gravitatiestraling uitgerekend:
Voor het vermogen geldt tevens:
Oftewel:
Dit combineer ik met vergelijking (1), het vermogen:
Omdat P een functie is van de hoek θ ga ik over van de
integratievariabele t naar θ:
Omdat het zwaartekrachtveld zwak is én omdat de snelheden niet-relativistisch zijn mag ik Newtonse
hemelmechanica gebruiken.
Daarom haal ik even wat vergelijkingen op van de pagina
hemelmechanica, om te beginnen die breuk dt/dθ
(vergelijking (91) op die pagina):
Hiermee wordt vergelijking (5):
Nu moet ik r nog schrijven als functie van de hoek θ.
Daarvoor gebruik ik vergelijking (58) van de pagina
hemelmechanica:
Hiermee wordt vergelijking (7):
Nu ga ik haakjes wegwerken:
De oplossing van de
integraal
van cos
2 x kun je vinden in de
tabel met integralen,
de oplossing van de
integraal
van cos
3 x kun je vinden in de
tabel met integralen
en de oplossing van de
integraal
van cos
4 x kun je ook vinden in de
tabel met integralen.
Dat brengt ons bij dit resultaat:
Aldus heb ik de uitgezonden energie als functie van de hoek θ gevonden.
De eerste term aan de rechterkant bevat alleen maar constanten, en daarom is het wel zinvol om de overige termen
even onder te brengen in een aparte functie:

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.001 oplopend tot e = 0.01 (de lichtblauwe lijn)

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.01 oplopend tot e = 0.1 (de lichtblauwe lijn)

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.1 oplopend tot e = 0.99 (de lichtblauwe lijn)

De grafiek van f (e, θ) voor e = 0 (de rode lijn),
in stappen van 0.1 oplopend tot e = 0.99 (de lichtblauwe lijn),
logaritmische verticale schaalverdeling
De grafieken laten duidelijk zien dat:
- de energie lineair toeneemt voor een cirkelvormige baan (e = 0, de rode lijn in bovenstaande grafieken),
- de energie zeer sterk toeneemt bij θ = 0 = 2π, dus tijdens de passage van het
periapsis waar de snelheid het hoogst is,
- de energie nagenoeg constant is bij θ = π, dus tijdens de passage van het
apoapsis waar de snelheid het laagst is,
- de energie zeer sterk toeneemt wanneer de
excentriciteit van de baan toeneemt.

De grafiek van f (e, θ) voor θ = 0.001

De grafiek van f (e, θ) voor θ = 0.001,
logaritmische verticale schaalverdeling

De grafiek van f (e, θ) voor θ = π

De grafiek van f (e, θ) voor θ = π,
logaritmische verticale schaalverdeling
Om de energie te vinden die gemiddeld per omloop uitgezonden wordt moet ik de energie, vergelijking (11),
sommeren én middelen over één omlooptijd:
De omlooptijd T vind ik ook op de pagina
hemelmechanica (vergelijking (61) op die pagina):
Dit vul ik in in vergelijking (13), de energie haal ik uit vergelijking (11), en omdat de energie een
functie is van θ verander ik de
grenzen in 0 en 2π:
Al die
sinustermen zijn gemiddeld over een hele
periode nul en mag ik daarom probleemloos verwijderen:
De eerste term aan de rechterkant bevat alleen maar constanten, en daarom is het weer zinvol om de overige termen
onder te brengen in een aparte functie:

De grafiek van g (e)

De grafiek van g (e),
logaritmische verticale schaalverdeling
Samengevat:
- de uitgestraalde energie als functie van de hoek:
- de uitgestraalde energie gemiddeld per omloop:
 c).
c).
 c).
c).































 Door naar het volgende vraagstuk: de tweelingparadox
Door naar het volgende vraagstuk: de tweelingparadox Terug naar het vorige vraagstuk: het vermogen van gravitatiestraling
Terug naar het vorige vraagstuk: het vermogen van gravitatiestraling Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie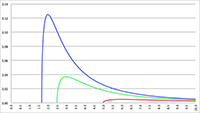 De integraal van
De integraal van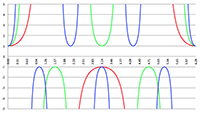 De integraal van
De integraal van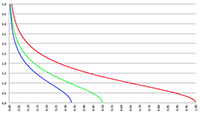 De integraal van
De integraal van De integraal van
De integraal van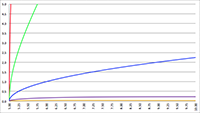 De integralen van
De integralen van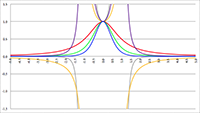 De integralen van
De integralen van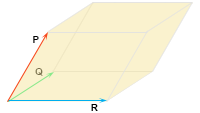 Vectoren, vraagstuk 6
Vectoren, vraagstuk 6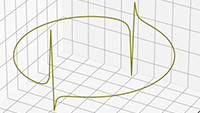 Vectoren, vraagstuk 51
Vectoren, vraagstuk 51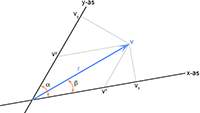 Covariante - en contravariante componenten van een vector
Covariante - en contravariante componenten van een vector Taylor-reeksen
Taylor-reeksen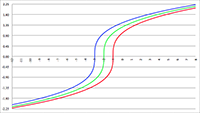 De Taylor-reeks van
De Taylor-reeks van Een reeks afsplitsen van
Een reeks afsplitsen van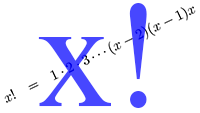 Faculteiten
Faculteiten Holomorfie van de functie
Holomorfie van de functie Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid
Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie
Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie De relativistische rotatie-energie van een massieve bol
De relativistische rotatie-energie van een massieve bol Een botsing met een zandkorrel
Een botsing met een zandkorrel Een analogie van het onzekerheidsprincipe van Heisenberg
Een analogie van het onzekerheidsprincipe van Heisenberg Terugkijkend vanaf je sterfbed, wat ga je NU doen?
Terugkijkend vanaf je sterfbed, wat ga je NU doen? De energie van gravitatiestraling
De energie van gravitatiestraling Een dag zonder verjaardagen
Een dag zonder verjaardagen Tijdsvertraging van een lichtstraal (2e orde benadering)
Tijdsvertraging van een lichtstraal (2e orde benadering) Tijdsvertraging van een lichtstraal (1e orde benadering)
Tijdsvertraging van een lichtstraal (1e orde benadering) Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein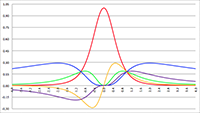 De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen