De invaltijd van een baksteen die in een zwart gat valt
Wanneer ik vanaf grote afstand een baksteen in een niet-roterend zwart gat laat vallen, hoe lang duurt het dan totdat
de baksteen de horizon passeert bezien vanuit een waarnemer die met de baksteen meebeweegt?

De baksteen nadert de horizon van het zwarte gat,
een kabouter heeft zichzelf gepromoveerd tot meebeweger
door zich aan de baksteen vast te laten ketenen

Ik laat vanaf grote afstand een baksteen in een zwart gat vallen en een kabouter, met een oranje mutsje, heeft zichzelf laten vastketenen aan de baksteen en zichzelf daarmee tot meebewegende waarnemer [Engels: comoving observer of free falling observer of rain observer (regendruppels zijn in vrije val als je de luchtweerstand verwaarloost)] gepromoveerd. Op het plaatje hiernaast zie je de kabouter, die zichzelf vrijwillig gemeld heeft, vastgeketend aan de baksteen. Hoeveel tijd verstrijkt er in zijn referentiekader, zijn referentiestelsel, zijn coördinatenstelsel, voordat hij de horizon van het zwarte gat passeert?
In dit vraagstuk heb ik de snelheid afgeleid van een baksteen die in een niet-roterend zwart gat valt. Vergelijking (6) van die pagina geeft de snelheid: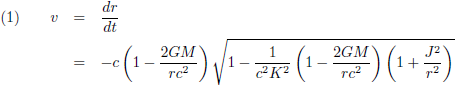
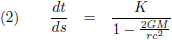
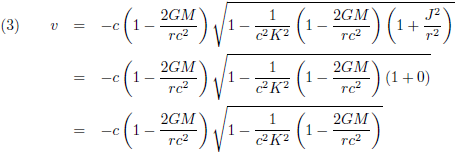
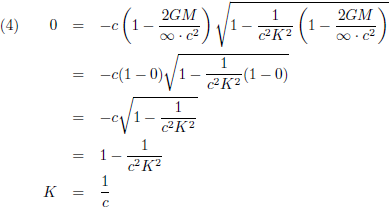
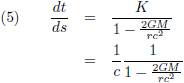
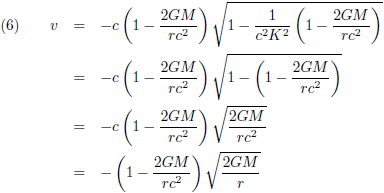
Ik haal even de Schwarzschild-oplossing (oftewel de Schwarzschild-metriek) op, want die is hier van toepassing:
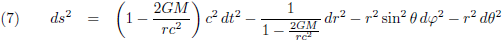
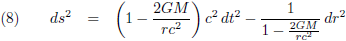
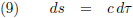
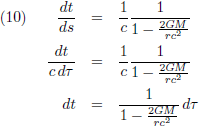
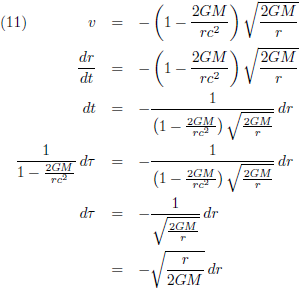
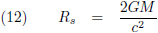
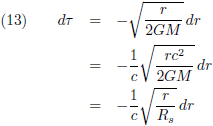
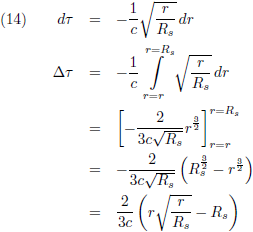

De grafiek van ∆τ
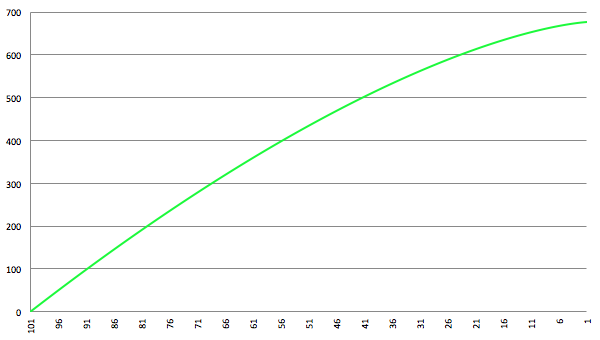
De grafiek van ∆τ
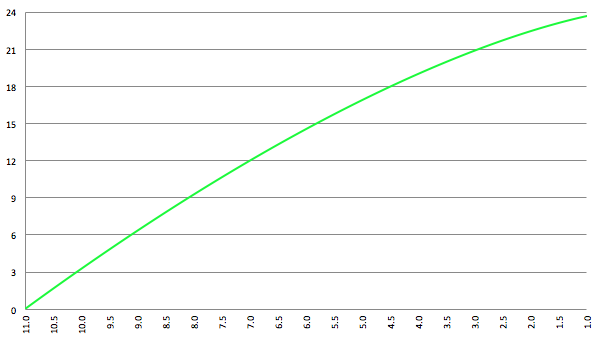
De grafiek van ∆τ
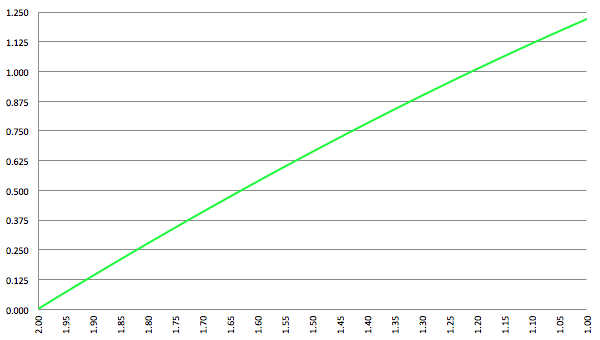
De grafiek van ∆τ
 Deze tabel geldt voor een niet-roterend zwart gat |
 Voor een verre stationaire waarnemer |
 Voor een nabije stationaire waarnemer |
 Voor een meebewegende waarnemer |
| De invaltijd van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking (= deze pagina) |
|
| De snelheid van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
Toon uitwerking |
| De versnelling van een baksteen die in een zwart gat valt |
Toon uitwerking |
Toon uitwerking |
Toon uitwerking |

 Door naar het volgende vraagstuk: de baan van een baksteen bij een zwart gat
Door naar het volgende vraagstuk: de baan van een baksteen bij een zwart gat Terug naar het vorige vraagstuk: de versnelling van een baksteen die in een zwart gat valt
Terug naar het vorige vraagstuk: de versnelling van een baksteen die in een zwart gat valt Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie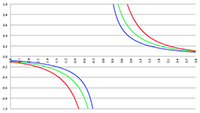 De integraal van
De integraal van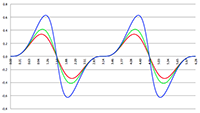 De integraal van
De integraal van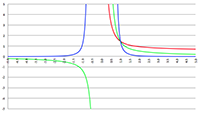 De integraal van
De integraal van De integraal van
De integraal van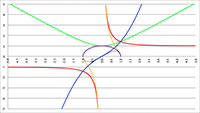 De integralen van
De integralen van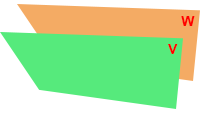 Vectoren, vraagstuk 15
Vectoren, vraagstuk 15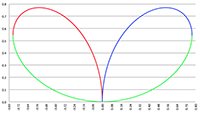 Vectoren, vraagstuk 60
Vectoren, vraagstuk 60 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT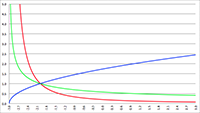 De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking Differentiëren van complexe functies
Differentiëren van complexe functies Holomorfie van de functie
Holomorfie van de functie Uitleg artikel algemene relativiteitstheorie: paragraaf 1
Uitleg artikel algemene relativiteitstheorie: paragraaf 1 Ruimtetijddiagrammen
Ruimtetijddiagrammen Wat maakt een zwart gat tot een zwart gat?
Wat maakt een zwart gat tot een zwart gat? De zwaartekracht van een homogene oblate ster
De zwaartekracht van een homogene oblate ster Vraagstukken algemene natuurkunde
Vraagstukken algemene natuurkunde De illusie van anorexia
De illusie van anorexia Vertellingen
Vertellingen Afbuiging van een lichtstraal (2e orde benadering)
Afbuiging van een lichtstraal (2e orde benadering) Afbuiging van een lichtstraal (1e orde benadering)
Afbuiging van een lichtstraal (1e orde benadering) Bewerkingen met reeksen
Bewerkingen met reeksen De Taylor-reeksen van
De Taylor-reeksen van De integralen van
De integralen van De integralen van
De integralen van De integralen van
De integralen van De massa van de atmosfeer
De massa van de atmosfeer Hyper-Catalan-getallen
Hyper-Catalan-getallen Een ontmoeting met aliens
Een ontmoeting met aliens Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen