Afbuiging van een lichtstraal volgens Einstein
Bereken de afbuiging van een lichtstraal, onder invloed van de zwaartekracht, zoals Einstein dat gedaan heeft.
Tegenwoordig is de berekening van de afbuiging van een lichtstraal een standaardexercitie in ieder boek
over algemene relativiteitstheorie, waarbij men uitgaat van de
Schwarzschild-oplossing, vervolgens de
Euler-Lagrange-vergelijking inzet, en daarna de
resulterende differentiaalvergelijking in
een eerste orde benadering oplost.
Echter, toen Einstein in 1915 met zijn algemene relativiteitstheorie kwam was er nog helemaal geen exacte
oplossing beschikbaar en Einstein heeft daarom flink moeten ‘knutselen’ om het antwoord te vinden.
Hij doet daar redelijk uitgebreid verslag van in zijn artikel en dat pad gaan we hier volgen.
- Geïnteresseerd in het oorspronkelijke artikel?
Stuur mij dan een email (karel@voorbijeinstein.nl)
met als onderwerp “PDF bestand 020106000088” en ik stuur je de file (gratis) toe.
Opmerking: ik kan inderdaad ook zorgen dat je het artikel rechtstreeks van mijn website kunt downloaden,
maar dan schend ik auteursrechten.
De algemene relativiteitstheorie was destijds een gloednieuw stuk natuurkunde en bepaalde notaties, die
tegenwoordig redelijk standaard zijn, waren er toen nog niet.
Daarom moeten we even rekening houden met een aantal zaken:
- tegenwoordig gebruiken we Griekse letters als indices om vier dimensies aan te geven en Latijnse indices om
alleen de drie ruimtelijke dimensies aan te geven, ten tijde van Einstein was dat nog geen gemeengoed,
- tot op de dag van vandaag gebruiken verschillende auteurs verschillende tekens (plussen of minnen)
voor allerlei grootheden, dus her en der staat er een minteken meer of minder, bijvoorbeeld bij het ruimtetijdinterval,
- Einstein gebruikt de vierde coördinaat, x4, voor de tijd terwijl tegenwoordig x0
gebruikelijk is,
- Einstein is slordig, dus bijvoorbeeld indices staan niet altijd op de juiste hoogte, en bovendien
bevat zijn artikel tientallen fouten.

Principia
Het is 1687 wanneer de eerste uitgave (350 exemplaren) van het boek Philosophiae Naturalis Principia Mathematica,
kortweg Principia, van Isaac Newton beschikbaar komt.
In dit boek beschrijft Newton onder andere de zwaartekracht en hij laat de wereld tevens zijn gravitatiewet na:
Nu, ruim driehonderd jaar later, leert iedere scholier op het voortgezet onderwijs met natuurkunde in zijn/haar pakket nog steeds de
werking van de zwaartekracht middels die gravitatiewet van Newton.
Ook echte wetenschappers maken in overgrote meerderheid nog altijd gebruik van Newton’s wet, want die is simpel en voldoet eigenlijk altijd.
Einstein wist dit uiteraard en besefte terdege dat zijn relativiteitstheorie in ‘gewone huis-tuin-en-keuken-gevallen’ in overeenstemming
diende te zijn met de gravitatiewet van Newton om de doodeenvoudige reden dat berekeningen met Newton’s wet heel erg goed overeenstemmen
met de werkelijkheid.
Oftewel, de gravitatiewet van Newton dient als hele goede benadering uit de bus te komen voor de relativiteitstheorie van Einstein.
Einstein wist ook dat de speciale relativiteitstheorie een specifiek geval van de algemene relativiteitstheorie is,
en zich daardoor kenmerkt dat de metrische tensor g in dat geval de volgende vorm aanneemt:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Met andere woorden: in een dergelijk geval is iedere gravitatiewerking afwezig.
Een benadering die dichter bij de werkelijkheid komt is wanneer de g
μν maar een beetje van nul of één afwijken,
waarbij “een beetje” door Einstein gedefinieerd wordt als een eerste orde afwijking.
Afwijkingen van tweede - en hogere orde worden dus verwaarloosd en hij noemt dit het eerste uitgangspunt van de benadering
(de benadering van de algemene relativiteitstheorie die moet leiden tot de gravitatiewet van Newton).
Verder nemen we aan dat de g
μν in het oneindige de waarden van vergelijking (2)
aannemen en dat alle afwijkingen van de g
μν (afwijkingen van vergelijking (2)) het gevolg zijn van massa
die zich op eindige afstanden bevindt (waarbij ‘eindig’ natuurlijk een rekbaar begrip is, maar Einstein gaat ervanuit
(en ik ook) dat je gevoelsmatig wel snapt wat hij bedoelt).
Met deze aannames zouden we op Newton’s theorie uit moeten komen, maar Einstein komt met nog een tweede uitgangspunt.
Volgens de volgende wet van Newton bepaalt de kracht die wordt uitgeoefend op een object de versnelling (snelheidsverandering)
van dat object:
Volgens bovenstaande wet van Newton beweegt ieder object waar geen kracht op wordt uitgeoefend (F = 0) zich met constante snelheid
langs een rechte lijn (en in de Newtonse benadering is de massa constant):
Dit gaan we vergelijken met de vergelijking van een geodetische lijn:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

In onze dagelijkse ervaring treden alleen maar snelheden op die veel kleiner zijn dan de snelheid van het licht
(v

c) en dit betekent dat zowel voor een eerste - als
tweede orde benadering geldt:
We kunnen daarom tevens stellen dat:
Snelheden hebben dan de bekende vorm:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

De componenten van de snelheid (datgene wat in vergelijking (8) onder het
wortelteken tussen de haakjes staat,
oftewel de vergelijkingen (7)) zijn dan tevens als ‘klein’ aan te merken (klein ten opzichte van de lichtsnelheid).
Dat dx
4/ds bij goede benadering gelijk is aan één is het tweede uitgangspunt van Einstein’s benadering
(Einstein gebruikt x
4 voor de tijdcoördinaat, tegenwoordig gebruikt men daar x
0 voor).
Samengevat:
- de gμν wijken slechts tot eerste orde af van nul of één,
- dx4/ds is gelijk aan één.
Omdat volgens de tweede aanname geldt dat ds ≈ dx
4 gaat vergelijking (5) over in:
In de rechterterm van deze vergelijking wordt gesommeerd over de indices μ en ν die allebei de waarden 1, 2, 3, 4 doorlopen
(dus zestien combinaties in totaal).
Maar aangezien we net geconcludeerd hebben dat de componenten van de snelheid, volgens vergelijking (8), klein zijn (ten opzichte
van de lichtsnelheid) zal de term waarbij μ = ν = 4 dominant zijn.
We kunnen dus ook schrijven:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

En dat kan ik ook schrijven als:
Vergelijking (11) ga ik splitsen:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Dus waar Newton zegt dat een vrij deeltje (een deeltje waar geen krachten op inwerken) een rechte lijn volgt:
Daar zegt Einstein dat een vrij deeltje een geodetische lijn volgt:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Het is nu wel heel interessant om vergelijking (12a) aan een nader onderzoek te onderwerpen.
Ik ga daarom die vergelijking nog verder uitschrijven:
Vervolgens stelt Einstein ook nog dat het gravitatieveld quasi-statisch is, want we hebben hiervoor immers aangenomen dat alle snelheden
ver beneden die van de lichtsnelheid liggen (dus ook de snelheden van de massa’s die zwaartekracht genereren).
Daarom kan ik de eerste term aan de rechterkant van bovenstaande vergelijking verwaarlozen omdat dat een
afgeleide naar de tijd
(x
4 = t) is:
Het is tegenwoordig gebruikelijk dat Latijnse indices alleen over de drie ruimtelijke dimensies ‘lopen’ en Griekse indices over alle
vier dimensies.
Dat was in de tijd van Einstein nog niet het geval en daarom zal ik bovenstaande vergelijking even schrijven volgens Einstein’s notatie:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Door hier Newton’s theorie tegenover te zetten
met zwaartekracht ontstaat (waarbij ik naar keuze m
1 of
m
2 uitdeel, en het minteken komt erbij omdat het zwaartekrachtveld richting de oorsprong gericht is):

Het zwaartekrachtveld van een puntmassa
(de z-richting is niet getekend)
Het zwaartekrachtveld is een conservatief veld en er bestaat dus een potentiaalfunctie voor
het zwaartekrachtveld en die noem ik φ:

In een conservatief veld kost de route van A naar B altijd evenveel energie
Dan kan ik (16) ook schrijven als:
Door de vergelijkingen (15) en (18) met elkaar te vergelijken kom ik tot:
Vervolgens merkt Einstein terecht op dat het op zich merkwaardig is dat in eerste benadering alleen de component g
44
van de metrische tensor de uitkomst van de bewegingsvergelijking (15) bepaalt.
Nu richt Einstein zich op de veldvergelijkingen:

 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

De volgende stap is om een benadering te vinden voor de energietensor T.
In
paragraaf 19 (van het artikel van Einstein) vonden we:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

De indices α en β doorlopen ook hier allebei de waarden 1, 2, 3, 4 (dus zestien combinaties in totaal), maar net zoals
in het voorgaande is de dominante component die waarbij α = β = 4.
Bovendien is de energie van de materie (
E = mc2)
normaliter dominant over de energie van de druk (dus ρ

p).
We kunnen dus ook schrijven:
Oftewel:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Dit tussenresultaat vul ik in in vergelijking (20a):
Vervolgens schrijf ik de Christoffel-symbolen iets anders op:
Nu ga ik de Christoffel-symbolen omschrijven van de tweede soort naar de eerste soort:
Voor de Christoffel-symbolen van de eerste soort geldt:
Je zou dus kunnen zeggen dat de eerste term aan de linkerkant van vergelijking (26) g
μν’s bevat
tot de tweede
macht
en de tweede term bevat g
μν’s
tot de vierde
macht.
Omdat de g
μν’s die niet op de
hoofddiagonaal liggen heel klein zijn zal de
eerste term daarom veel meer bijdragen dan de tweede term.
Bij goede benadering kunnen we dus stellen dat:
Omdat de componenten van de metrische tensor die op de
hoofddiagonaal liggen dominant zijn gaat dit over in:
 Oorspronkelijke vergelijking uit het artikel van Einstein (voor het linkerlid):
Oorspronkelijke vergelijking uit het artikel van Einstein (voor het linkerlid):

Er zit helaas niets anders op dan dit helemaal uit te schrijven:
We kiezen natuurlijk weer voor die termen waarvoor geldt dat μ = ν = 4:
En om dezelfde reden als hiervoor gooien we alle
afgeleiden naar de tijd (x
4 = t) weer overboord:
 Oorspronkelijke vergelijkingen uit het artikel van Einstein:
Oorspronkelijke vergelijkingen uit het artikel van Einstein:


Met een kleine aanpassing kan ik ook schrijven:
En door daar vergelijking (19) in in te vullen kom ik tot:
De evenredigheidsconstante

is (Einstein heeft c = 1 gesteld, maar slordig
als hij is doet hij dat niet consequent, bovendien haalt hij

en de gravitatieconstante G (waarvoor hij de letter K gebruikt) door elkaar):
Waarmee vergelijking (34) overeenkomt met de vergelijking van Poisson die we in
paragraaf 16 (van het artikel van Einstein) al tegenkwamen:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

We hebben gezien dat van de zestien g
μν-componenten (waarvan er tien onafhankelijk zijn)
bij eerste benadering alleen de component g
44 de bewegingsvergelijking van een object in een zwaartekrachtveld bepaalt:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Daarbij gingen we ervanuit dat de g
μν maar ‘een beetje’ afwijken van de volgende waarden:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Echter, we zijn er telkens vanuit gegaan dat:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Helemaal uitgeschreven ziet de
determinant
g er zo uit:
Einstein merkt daarom terecht op dat behalve g
44 er ook nog andere componenten van de metrische tensor moeten afwijken van
de waarden van vergelijking (2) in het geval dat we een eerste orde benadering uitvoeren.
Oftewel, we gaan proberen te vinden hoe (de kleine afwijkingen van) de componenten van de metrische tensor g er uit zien:
Einstein gaat uit van een puntmassa die zich in de oorsprong van één of ander coördinatenstelsel bevindt.
Die puntmassa genereert uiteraard een zwaartekrachtveld en dit veld zal symmetrisch zijn in de x, y en z-richting,
want er is verder geen enkel ander object aanwezig die die symmetrie zou kunnen verstoren.

Het zwaartekrachtveld van een puntmassa
(de z-richting is niet getekend)
Indien we denken volgens Newton dan heeft het veld de volgende potentiaal:
Waarbij r gelijk is aan (in een Cartesisch stelsel):
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Ik bepaal even wat
partiële afgeleiden:
Dan kan ik voor het interval schrijven:
Hieruit kunnen we de volgende g
μν-componenten pikken:
Oftewel, in een Euclidische ruimte zou ik hebben:
En alle andere componenten van de metrische tensor zouden dan nul zijn, maar het voorafgaande laat zien dat ik dit breder kan trekken
(dus niet-Euclidisch en niet-Cartesisch beschouwd):
Omdat de puntmassa zich in de oorsprong bevindt en in de tijd gezien niets doet, het veld is dus statisch, kan ik stellen dat:
Met de wijsheid van de vergelijkingen (45) en (46) kan ik de tensor g van vergelijking (39) invullen:
Hierin zijn a en b nog onbekende functies.
Dat de ruimtelijke componenten van de g
μν (μ = 1, 2, 3 en ν = 1, 2, 3) dezelfde afwijking van één hebben
is logisch gezien het feit dat we een volkomen symmetrische situatie hebben rondom de oorsprong.
De voor de hand liggende vraag is natuurlijk: hoe vinden we nu a en b?
Daarvoor gooien we dit probleem over een hele andere boeg.
Binnen de algemene relativiteitstheorie heb ik deze metrische tensor:
En binnen de speciale relativiteitstheorie heb ik deze metrische tensor:
We gaan nu het volgende doen.
Omdat we ervanuit gaan dat de g
μν-componenten maar een beetje afwijken van de η
μν-componenten
stelt ons dit in staat een zogenaamde
lineaire benadering, oftewel een
eerste orde benadering, toe te passen.
Om te beginnen stel ik:
Of voluit geschreven:
In het vervolg dat nu gaat komen neem ik alleen de eerste ordes mee van de
verstoringsparameter ε (we doen immers een eerste orde
benadering), dus
kwadraten
en hogere
machten ga ik verwaarlozen.
Door die verwaarlozingen, die in het hiernavolgende deel gaan plaatsvinden, gaat de sommatieconventie niet meer eenduidig werken.
De sommatieconventie zegt dat er in iedere term van een vergelijking gesommeerd moet worden over de index die precies tweemaal voorkomt,
éénmaal laag en éénmaal hoog, en die duidelijkheid verdwijnt wanneer we gaan verwaarlozen.
Daarom voeg ik tot nader order de sommeringstekens toe zodat er geen verwarring kan ontstaan.
En ik wil er nogmaals op wijzen dat Griekse indices over vier dimensies lopen en Latijnse indices alleen over de drie ruimtelijke dimensies.
De Riemann-tensor luidt:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Door daar een contractie op uit te voeren brengt ons dat bij:
De laatste twee termen (met de vermenigvuldigingen van de Christoffel-symbolen) genereren
kwadraten van de verstoringsparameter ε en in de
lineaire benadering waar we nu mee bezig zijn gooi ik die dus overboord:
In
paragraaf 14 (van het artikel van Einstein)
heeft Einstein de eis geformuleerd dat de bovenstaande tensor verdwijnt (nul wordt) indien er geen massa aanwezig is.
En omdat we het hier hebben over een puntmassa in de oorsprong is er verder helemaal nergens massa.
Oftewel, buiten de oorsprong is de tensor B
μν gelijk aan nul:
Waarmee vergelijking (54) wordt:
In
paragraaf 12 (van het artikel van Einstein) kwam langs:
Hiermee schrijf ik vergelijking (56) om:
We kunnen de
determinant g bepalen als volgt:
Echter, omdat we
kwadraten
en hogere
machten
van ε verwaarlozen reduceert dit tot de eerste term:
Dit resultaat stoppen we in (58):
In de tabel met Taylor-reeksen vinden we:
Als eerste orde benadering geldt dan:
Dit gegeven gebruik ik om vergelijking (60) te vereenvoudigen:
Vervolgens ga ik met de tweede term van de bovenstaande vergelijking knutselen:
De
afgeleiden
van η
μν zijn uiteraard nul, omdat η
μν alleen maar constanten (getallen) bevat.
Daardoor reduceert (64) tot:
De termen met ε
2 kunnen we verwaarlozen en daarna kunnen we ε zelfs uitdelen:
Nu hebben we een vergelijking waarin de parameter ε helemaal niet meer voorkomt!
Het is ook te zien dat alle componenten waarbij α ≠ β nul worden (want η
αβ is dan nul).
Verder ga ik nu onderscheid maken tussen α = β = 4 (= t) en de ruimtelijke dimensies:
We hebben een statische situatie, dus alle
afgeleiden naar de tijd zijn nul en vallen eruit:
Het is op dit punt wel even interessant om te kijken naar de situatie μ = ν = 4 (= t), en alle
afgeleiden naar de tijd er gelijk weer
uit te kieperen:
Hetgeen helemaal overeenkomt met wat we eerder al vonden:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Want we beschouwen nu de ruimte buiten de puntmassa in de oorsprong, en aangezien daar geen massa is, en de massadichtheid dus gelijk aan
nul is, zijn de vergelijkingen (32) en (69) equivalent.
Voor extra duidelijkheid:
Uitgaande van de vergelijkingen (69) en (70) kijk ik vervolgens naar de tensor van vergelijking (47) en dan volgt daar het volgende uit:
Dus we zijn alvast iets wijzer geworden over de onbekende b.
Ik wil nogmaals vermelden dat we een volkomen statische situatie hebben, dus er beweegt niets, er roteert niets, alles ‘staat stil’.
Dan ligt het voor de hand om aan te nemen dat er geen ‘kruisbestuiving’ plaatsvindt tussen de ruimtelijke dimensies en dat in
de metrische tensor alle componenten die niet op de
hoofddiagonaal liggen gelijk aan nul zijn.
Vervolgens keren we terug naar vergelijking (68) en kijken we alleen naar de componenten op de
hoofddiagonaal.
Daarvoor stel ik ν = μ:
Ik ga dit nog iets verder uitwerken en ik vul de componentwaarden van de tensor van vergelijking (47) in (voor zover mogelijk):
Tenslotte sommeer ik over μ = 1, 2, 3, 4:
Volgens goed gebruik gooien we de
afgeleiden naar de tijd eruit:
Omdat er geen ‘kruisbestuiving’ plaatsvindt tussen de ruimtelijke dimensies betekent dat dat in bovenstaande vergelijking alle termen
tussen de haken nul zijn.
Dan gaat (75) over in:
Oftewel, afgezien van eventuele constanten:
Einstein gaat hier zomaar vanuit in zijn artikel en ik vond dat een beetje kort door de bocht, daarom deze vrij lange omweg.
Ik vul dit vervolgens in in de tensor van vergelijking (47):
Nu hebben we de onbekende b geëlimineerd en rest ons nog de taak om een uitdrukking voor a te vinden.
In vergelijking (71) vonden we dat ∆b = 0, en volgens (76) en (77) geldt dan ook dat ∆a = 0.
Vergelijking (19) leerde ons:
Hierin is φ de potentiaalfunctie van het zwaartekrachtveld volgens de newtoniaanse zwaartekracht.
Dit stelt ons in staat om a te bepalen:
Oftewel, afgezien van eventuele constanten:
Nu maken we nogmaals gebruik van vergelijking (17):
Voor a vind ik dan:
Ik stel:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Einstein zit hier even een factor twee verkeerd en schrijft 8π in plaats van 4π, maar verderop doet hij het wel goed.
Nu kan ik voor a schrijven:
En door dit vervolgens in te vullen in de metrische tensor van vergelijking (78) krijg ik tenslotte:
Of in indexnotatie:



 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Einstein merkt nog op dat met de bovenstaande tensor (84) aan de veldvergelijkingen voldaan wordt, in een eerste orde benadering wel te verstaan.
Dat heb ik hiervoor uitgebreid laten zien, want ik ben uitgegaan van een lineaire benadering (= eerste orde), dus dat klopt inderdaad (uiteraard).
Dan stelt Einstein het gedrag van lichtstralen in een zwaartekrachtveld aan de orde.
Een afstand in de vierdimensionale ruimtetijd, het interval, binnen de speciale relativiteitstheorie is:
Het lichtachtige interval, het interval van een lichtstraal, is gelijk is aan nul.
Dan wordt vergelijking (86):
En indien we een klein stukje ruimtetijd beschouwen wordt dit:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Het equivalent van (87) binnen de algemene relativiteitstheorie is:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Indien de richting van de lichtstraal bekend is dan betekent dit dat de verhouding tussen dx, dy en dz bekend is.
Of in indexnotatie geschreven: de verhouding tussen dx
1, dx
2 en dx
3:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Met behulp van vergelijking (89) opent dat de deur om deze grootheden te bepalen:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Dus dat gaan we natuurlijk doen.
Door te stellen dat:
Vervolgens ga ik vergelijking (89) helemaal uitschrijven en ook gebruik maken van de bovenstaande twee vergelijkingen:
Nu heb ik een eenvoudige
tweedegraads vergelijking
waaruit ik de snelheid v
x, de snelheid in de x-richting, kan oplossen.
En door die daarna te vermenigvuldigen met p respectievelijk q vind ik gemakkelijk de snelheden v
y en v
z en
heb ik dus alle componenten van de snelheid v gevonden.
In een Euclidische ruimte (en een heel klein stukje ruimte is altijd Euclidisch, want we komen daar in het limietgeval van de
algemene relativiteitstheorie zijnde de speciale relativiteitstheorie) kan ik dan voor de snelheid schrijven:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Dit kan ik ook schrijven als:
We hebben inmiddels geleerd dat zwaartekracht de ruimte vervormt.
Maar anderzijds hebben we de heilige graal van het elektromagnetisme die zegt dat de snelheid van het licht een absolute constante is.
Indien we te maken hebben met een gekromde ruimte dan zijn de componenten van de metrische tensor, de g
μν, geen
constanten meer maar variabelen.
Volgens vergelijking (92) zal v
x daardoor ook variabel worden en vergelijking (94) zegt dat het daardoor onvermijdelijk
is dat p en q ook variabel worden om de constante lichtsnelheid veilig te stellen.
En omdat p en q de richting bepalen van de lichtstraal betekent dit dat zwaartekracht een lichtstraal laat
afbuigen.
Ieder antwoord dat de mensheid vindt leidt logischerwijs tot de volgende vraag en dat is in dit geval: hoeveel dan?
Hoeveel wordt een lichtstraal afgebogen door de zwaartekracht van een bepaald voorwerp?
Dat gaan we nu berekenen.
In het artikel van Einstein gaat dat vergezeld van een plaatje, het enige plaatje in het artikel, en die heb ik gekopieerd en hieronder
geplaatst:
We gaan uit van een x
1-x
2-vlak (een x-y-vlak) met daarin een lichtstraal die de x
1-as (de x-as) kruist
precies parallel aan de x
2-as (de y-as).
De x
3-as (de z-as) staat loodrecht op het papier en die doet niet mee in het verhaal.
In de oorsprong van dit assenstelsel bevindt zich een puntmassa m en de lichtstraal passeert deze puntmassa op een afstand ∆.
De lichtstraal dendert voort in de richting van zijn snelheid γ (in bovenstaande figuur is dat de
x
2-richting op het moment dat de lichtstraal de x
1-as kruist) en de richting die hier
loodrecht op staat noemen we n (in bovenstaande figuur is dat de x
1-richting op het moment dat de lichtstraal
de x
1-as kruist).
Een afbuiging in een bepaalde richting betekent dat er in die richting een kracht werkt en dus ook een versnelling.
Versnelling is gedefinieerd als:
Of in dit geval:
De afbuiging van de lichtstraal vindt uiteraard plaats in de richting n (of −n) en als we willen weten
hoeveel de
lichtstraal afbuigt, en niet
hoe snel de lichtstraal afbuigt, dan zijn we geïnteresseerd in de volgende grootheid
(met een minteken, want de afbuiging vindt plaats in de richting van de puntmassa):
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

De richting loodrecht op de voortplantingsrichting van de lichtstraal is x
1, en omdat de lichtsnelheid zeer groot is
zal de afbuiging van de lichtstraal gering zijn en staat x
1 bij goede benadering de hele tijd loodrecht op de lichtstraal.
Daarom kunnen we voor (97) ook schrijven:
De afbuiging van de lichtstraal terwijl die een stukje dx
2 aflegt is dan:
Waarmee de totale afbuiging van de lichtstraal wordt:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Goed, het is weer tijd om te knutselen.
Allereerst pak ik vergelijking (92):
Omdat er in de z-richting niets gebeurt is q = 0 en houden we dit over:
Een blik op de metrische tensor van (85) herinnert ons eraan dat g
i4 = 0 waardoor we nog wat termen kunnen wegstrepen:
Ik heb dy en dz middels p en q aan dx gekoppeld, maar ik had ook dy als referentierichting kunnen nemen als volgt:
Vergelijking (102) had er dan op dit punt zo uitgezien (dat mag je zelf narekenen):
Zoals ik hiervoor al aangaf staat x
1 bij goede benadering de hele tijd loodrecht op de lichtstraal en reist de lichtstraal
de hele tijd (ook bij goede benadering) in de richting van x
2.
Dat houdt in dat p = 0 en dan gaat (105) over in:
Dit ga ik gebruiken in (93):
Deze twee componenten kan ik aflezen uit de metrische tensor van (85):
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Dit resultaat ga ik vervolgens
partieel differentiëren
naar x
1, en voor de overzichtelijkheid gebruik ik in de rest van
deze berekening x
1 = x, x
2 = y en x
3 = z:
Nu kan ik de
integraal gaan uitrekenen en die
splits ik op in twee
integralen:
De oplossing van de linker
integraal
zoek ik op in de
tabel met integralen
en de oplossing van de rechter
integraal
zoek ik ook op in de
tabel met integralen.
Dat brengt ons bij dit tussenresultaat:
We weten dat z = 0:
En we weten dat de x-afstand tot de puntmassa gelijk is aan ∆:
Nu ga ik α invullen:
 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Einstein zit hier weer even een factor twee verkeerd en schrijft 4π in plaats van 2π, maar hij rekent het getal wel goed uit.









 c) en dit betekent dat zowel voor een eerste - als
tweede orde benadering geldt:
c) en dit betekent dat zowel voor een eerste - als
tweede orde benadering geldt:
































 p).
We kunnen dus ook schrijven:
p).
We kunnen dus ook schrijven:

















 is (Einstein heeft c = 1 gesteld, maar slordig
als hij is doet hij dat niet consequent, bovendien haalt hij
is (Einstein heeft c = 1 gesteld, maar slordig
als hij is doet hij dat niet consequent, bovendien haalt hij
 en de gravitatieconstante G (waarvoor hij de letter K gebruikt) door elkaar):
en de gravitatieconstante G (waarvoor hij de letter K gebruikt) door elkaar):









































































































































 Door naar het volgende vraagstuk: tijdsvertraging van een lichtstraal, 1e orde benadering
Door naar het volgende vraagstuk: tijdsvertraging van een lichtstraal, 1e orde benadering Terug naar het vorige vraagstuk: afbuiging van een lichtstraal, 2e orde benadering
Terug naar het vorige vraagstuk: afbuiging van een lichtstraal, 2e orde benadering Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Overzichtspagina relativiteitstheorie
Overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van De integralen van
De integralen van Vectoren, vraagstuk 6
Vectoren, vraagstuk 6 Vectoren, vraagstuk 51
Vectoren, vraagstuk 51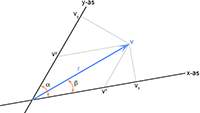 Covariante - en contravariante componenten van een vector
Covariante - en contravariante componenten van een vector Taylor-reeksen
Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van Een reeks afsplitsen van
Een reeks afsplitsen van Faculteiten
Faculteiten Holomorfie van de functie
Holomorfie van de functie Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid
Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie
Fouten in het oorspronkelijke artikel over de algemene relativiteitstheorie De relativistische rotatie-energie van een massieve bol
De relativistische rotatie-energie van een massieve bol Een botsing met een zandkorrel
Een botsing met een zandkorrel Een analogie van het onzekerheidsprincipe van Heisenberg
Een analogie van het onzekerheidsprincipe van Heisenberg Terugkijkend vanaf je sterfbed, wat ga je NU doen?
Terugkijkend vanaf je sterfbed, wat ga je NU doen? De tweelingparadox
De tweelingparadox De energie van gravitatiestraling
De energie van gravitatiestraling Een dag zonder verjaardagen
Een dag zonder verjaardagen Het vermogen van gravitatiestraling
Het vermogen van gravitatiestraling Tijdsvertraging van een lichtstraal (2e orde benadering)
Tijdsvertraging van een lichtstraal (2e orde benadering)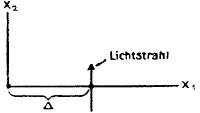 Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen