Vectoren, vraagstuk 53
De (vlakke) kromme C is de grafiek van de functie:
 (ook wel bekend als kettinglijn)
(ook wel bekend als kettinglijn)

- Geef een parametervoorstelling van C.
- Bereken de booglengte van C voor t van 0 naar x.
-
Geef een parametervoorstelling van C.
Er staat in een wat onnatuurlijke notatie dat aan iedere t een cosh t gekoppeld wordt, oftewel in een notatie die meer vertrouwd is: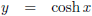 De simpelste parametrisering die we kunnen bedenken (en altijd werkt) is:
De simpelste parametrisering die we kunnen bedenken (en altijd werkt) is: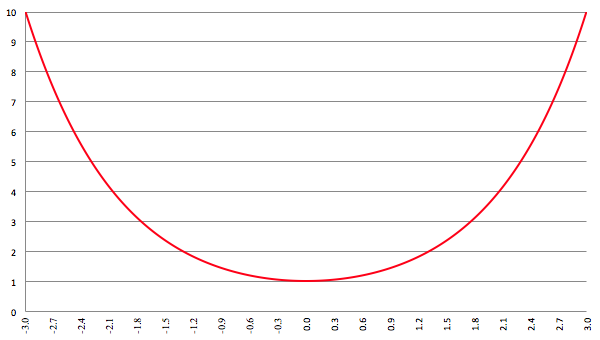
De grafiek van y = cosh xDan wordt y: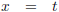 En hieruit volgt de parametrisering van de kromme C:
En hieruit volgt de parametrisering van de kromme C: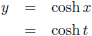
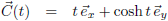
-
Bereken de booglengte van C voor t van 0 naar x.
Hiervoor bepalen we eerst de afgeleide:Daarmee kunnen we de booglengte s berekenen: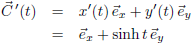
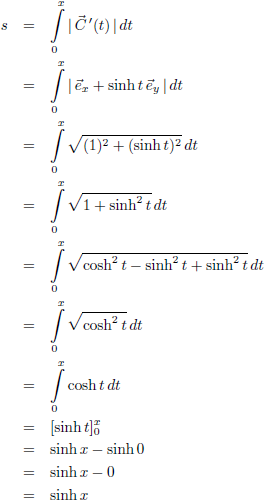
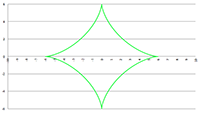 Door naar het volgende vraagstuk: vectoren, vraagstuk 54
Door naar het volgende vraagstuk: vectoren, vraagstuk 54 Terug naar het vorige vraagstuk: vectoren, vraagstuk 52
Terug naar het vorige vraagstuk: vectoren, vraagstuk 52 Overzichtspagina met vraagstukken
Overzichtspagina met vraagstukken Vraagstukken xref voor de UT
Vraagstukken xref voor de UT De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van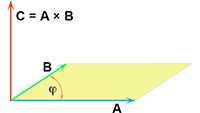 Inwendig product, uitwendig product en dyadisch product
Inwendig product, uitwendig product en dyadisch product Vectoren, vraagstuk 42
Vectoren, vraagstuk 42 Vectoren, vraagstuk 87
Vectoren, vraagstuk 87 Taylor-reeksen
Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De convergentie van een reeks
De convergentie van een reeks De stelling van Green
De stelling van Green Holomorfie van de functie
Holomorfie van de functie Integreren van complexe functies
Integreren van complexe functies Uitleg artikel algemene relativiteitstheorie: paragraaf 15
Uitleg artikel algemene relativiteitstheorie: paragraaf 15 Afleiding van de Reissner-Nordström-oplossing
Afleiding van de Reissner-Nordström-oplossing De pijn als je in een zwart gat valt
De pijn als je in een zwart gat valt Het modelleren van de dichtheid van de Zon
Het modelleren van de dichtheid van de Zon De Boltzmann-verdeling
De Boltzmann-verdeling De illusie van de grote gevaren
De illusie van de grote gevaren De tweelingparadox
De tweelingparadox De energie van gravitatiestraling
De energie van gravitatiestraling Een dag zonder verjaardagen
Een dag zonder verjaardagen Het vermogen van gravitatiestraling
Het vermogen van gravitatiestraling Tijdsvertraging van een lichtstraal (2e orde benadering)
Tijdsvertraging van een lichtstraal (2e orde benadering) Tijdsvertraging van een lichtstraal (1e orde benadering)
Tijdsvertraging van een lichtstraal (1e orde benadering) Afbuiging van een lichtstraal volgens Einstein
Afbuiging van een lichtstraal volgens Einstein De integralen van
De integralen van Een andere manier van leven
Een andere manier van leven Een reeks afsplitsen van een functie
Een reeks afsplitsen van een functie Overzichtspagina wiskunde
Overzichtspagina wiskunde Overzichtspagina natuurkunde
Overzichtspagina natuurkunde Overzichtspagina filosofie
Overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen