Klassieke periheliumprecessie
Trefwoorden/keywords: periheliumprecessie Mercurius/perihelion precession Mercury, klassiek/classical, niet-relativistisch/non-relativistic, volledige berekening/full calculation
Bereken de
periheliumprecessie
van de planeet Mercurius als gevolg van de zwaartekrachtinvloeden van de overige planeten.

Mercurius
(Credits: NASA)
Dit vraagstuk gaat over de wonderschone dans der planeten.
Van alle wiskundige problemen is dit ongetwijfeld één van de allermooiste en het laat op vele momenten
de schoonheid van de wiskunde zien.
Het perihelium,
het punt van dichtste nadering tot de Zon, van de planeet Mercurius verschuift, bij iedere omloop van
de planeet om de Zon, een klein beetje als gevolg van de zwaartekracht die de overige planeten op
Mercurius uitoefenen.
Dit verschuiven van het perihelium
noemen we
periheliumprecessie.
Voor de berekeningsmethode volg ik de methode van Gauss zoals hij die in 1818 uitgedacht heeft.
Deze methode is later, voor praktisch gebruik (rekenlinialen en logaritmetabellen), in enkele stappen verder
uitgewerkt door George Hill tijdens de tweede helft van de negentiende eeuw en tenslotte toegepast door
Eric Doolittle in 1912.
Doolittle heeft de volledige berekening uitgevoerd van de verstoringen die de planeten Venus, Aarde, Mars,
Jupiter, Saturnus, Uranus en Neptunus (de dwergplaneet Pluto was toen nog niet ontdekt) uitoefenen op de
baan van Mercurius.
Dit gebeurde met pen en papier, want computers bestonden er toen nog niet.
Helaas vermeldt het verhaal niet hoeveel mensen er daadwerkelijk bezig geweest zijn, en hoe lang, om dit
intense monnikenwerk uit te voeren.
- Geïnteresseerd in het oorspronkelijke artikel?
Stuur mij dan een email (karel@voorbijeinstein.nl)
met als onderwerp “PDF bestand 020204000006” en ik stuur je de file (gratis) toe.
Omdat dit Mercuriusvraagstuk nogal een uitgebreid verhaal is heb ik het onderverdeeld in vier hoofdstukken
(als je de wiskunde wilt overslaan dan raad ik aan om gelijk naar hoofdstuk drie te gaan):
- Afleiding van de vergelijkingen
- Hoe de berekening uit te voeren
- Berekeningen en resultaten
- Geschiedenis, conclusie en vooruitblik
Afleiding van de vergelijkingen
- Afleiding van de vergelijkingen
- Hoe de berekening uit te voeren
- Berekeningen en resultaten
- Geschiedenis, conclusie en vooruitblik
Ik maak gebruik van de vergelijkingen die ik heb afgeleid op de pagina’s
hemelmechanica en
seculaire verstoringen
(ik ga hierna ook refereren aan deze pagina’s).
Om te beginnen grijp ik terug op vergelijking (36) van de pagina
seculaire verstoringen, want dat is de
vergelijking die aangeeft hoe je de
periheliumprecessie
moet berekenen en daarom tevens mijn startpunt:
De vergelijkingen (7) van de pagina
seculaire verstoringen zijn de componenten
van de verstorende kracht in het x
*-y
*-z
*-stelsel als functie van de componenten
van de verstorende kracht in het x-y-z-stelsel (in de kracht in de z
*-richting zijn we niet geïnteresseerd
omdat die geen invloed heeft op de
periheliumprecessie,
zie de vergelijking hierboven):
De componenten van de verstorende kracht in het x-y-z stelsel kennen we ook (de vergelijkingen (4) van de pagina
seculaire verstoringen):
Waarbij voor de
verstoringsfunctie Θ geldt
(vergelijking (17) van de pagina
hemelmechanica):
Om de
periheliumprecessie
te berekenen zal vergelijking (1)
geïntegreerd
en gemiddeld moeten worden over een totale omloop van m
1:
Middels vergelijking (88) van de pagina
hemelmechanica
maakten we kennis met de
middelbare anomalie:
Hierin is n de
gemiddelde dagelijkse beweging.
Indien ik over een totale omloop praat dan staat er dus:
Door de
differentiaal te nemen van (6)
ontstaat:
Door de vergelijkingen (7) en (8) te combineren krijg ik:
En dit vul ik in in (5):
Volgens vergelijking (89) van de pagina
hemelmechanica kunnen we M schrijven als functie
van de
excentrische anomalie
E als volgt:
Waardoor (10) overgaat in:
Op deze manier vinden we per saldo de
periheliumprecessie
nadat planeet p
1 één omloop heeft voltooid.
Maar terwijl p
1 een omloop aflegt zijn de verstorende planeten uiteraard ook bezig met hun omlopen
om de Zon.
Dus de hoek E varieert, maar tegelijkertijd varieert ook de hoek E van iedere verstorende planeet.
Dit vereist dat we dat in vergelijking (12) gaan inbrengen.
Om te beginnen gaan we uit van één verstorende planeet, p
2, waardoor de
verstoringsfunctie Θ
wordt:
Het optellen van de invloeden van de diverse planeten (het sommeringsteken dat er eerst nog bij stond) stellen we
uit tot later waardoor (12) wordt:
Dat sommeringsteken ga ik niet de hele tijd meeslepen, dus die haal ik gelijk weer weg want het is nogal wiedus
dat we aan het eind de verstorende invloeden van alle planeten bij elkaar op moeten tellen.
En ik moet nauwkeuriger worden in mijn aanduidingen van wat er bij p
1 respectievelijk p
2
hoort door het toevoegen van indices:
We hebben dus een planeet, p
1, die de verstorende invloed ondergaat en één planeet, p
2, die
de verstorende invloed uitoefent.
Deze verstorende invloed is recht evenredig met de massa van p
2 (zie vergelijking (13)).
Ik stel het volgende:
Oftewel, de linkerleden van de bovenstaande drie vergelijkingen zijn de componenten van de verstorende kracht die
teweeg gebracht worden door één kilo m
2.
Vervolgens smeer ik de planeet p
2 uit over zijn gehele baan.
Er ontstaat daardoor een infinitesimaal dunne (oneindig dunne) elliptische ring met de magische eigenschap dat de
dichtheid van de ring op ieder punt evenredig is met de tijd dat de niet-uitgesmeerde-planeet in dat deel van de
ring doorbrengt (niet nadenken hoe zoiets in de praktijk verwezenlijkt zou kunnen worden, dat doet nu niet ter zake,
dit is wiskunde).
Daardoor geldt:
De verstorende kracht die ieder infinitesimale stukje ring uitoefent is:
Door te
integreren krijg ik de verstorende invloed
die de totale ring uitoefent op p
1:
Vervolgens breng ik vergelijking (17) in:
Kortom, we doen de werkelijkheid geen enkel geweld aan door p
2 uit te smeren over de baan die
p
2 doorloopt. Met behulp van (9) en (11) kunnen we de vergelijkingen (20) omschrijven als volgt:
Hierdoor wordt vergelijking (15):
De vergelijkingen (85) van de pagina
hemelmechanica
leerden ons hoe we r kunnen schrijven als functie van de
excentrische anomalie E,
al dan niet in combinatie met de
werkelijke anomalie θ:
Voor latere doeleinden schrijf ik (23b) nog iets anders op:
Vergelijking (23a) stelt ons in staat om (22) als volgt te schrijven:
Ik licht die twee binnenste
integralen er uit:
Vergelijking (24) ziet er dan zo uit:
Volgens de vergelijkingen (16) van de pagina
hemelmechanica kunnen we de componenten van de
verstorende kracht in het x-y-z-stelsel ook als volgt schrijven (waarbij ik uitga van één verstorende planeet,
p
2, en ik vermenigvuldig ook nog met m
1 omdat de vergelijkingen uit versnellingen bestaan
en ik wil daar krachten van maken):
Ik wil het even hebben over de rechtertermen van de bovenstaande vergelijkingen, om te beginnen de rechterterm van de
x-component en die ga ik
integreren en middelen over één
omloop van p
2:
Omdat we het hier over krachten hebben moet het deel binnen de
integraal een versnelling zijn en kan ik dus
ook schrijven:
De snelheid van p
2 is op t = 0 en één omloop verder op t = T niet veranderd en dus levert het antwoord van
de
integraal nul op.
De rechtertermen van de vergelijkingen (27) kunnen in deze berekening daarom weggelaten worden (of heel netjes gezegd:
ze leveren geen bijdrage aan de
seculaire verstoring),
en dat levert voor de componenten van de verstorende kracht de volgende eenvoudiger vergelijkingen op:
We hebben voor wat betreft de componenten van de verstorende kracht dus alleen rekening te houden met de rechtstreekse
aantrekking tussen p
1 en p
2.
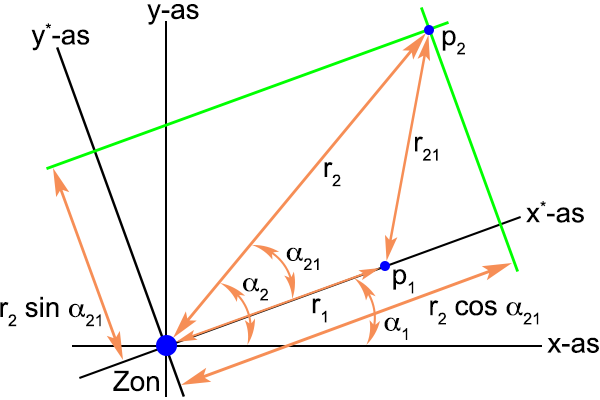
Ik heb daar even een plaatje van gemaakt:
Figuur 2
De vergelijkingen (6) van de pagina
seculaire verstoringen
geven aan hoe we x-y-z-coördinaten kunnen omrekenen naar x
*-y
*-coördinaten:
Door dit te combineren met (30) levert dat het volgende op:
Ik ga gebruik maken van het
inwendig product
van twee
vectoren A en
B:
Hiermee kan ik (32) omschrijven als volgt:
Hetgeen we ook relatief simpel kunnen aflezen uit figuur 2.
Ik ga op zoek naar de andere component van de verstorende kracht waarbij ik onderweg gebruik maak van de
verschilformules
(van twee willekeurige hoeken) uit de
goniometrie:
En ook dit leest gemakkelijk af uit figuur 2.
Voor de totale verstorende kracht geldt uiteraard:
Hier verschijnt uiteraard weer de zwaartekrachtwet van Newton en op deze manier heb ik gecontroleerd dat we nog
op het goede spoor zitten.
Ik heb tijdens deze laatste afleiding trouwens gebruik gemaakt van de
cosinusregel.
Ik heb nogmaals de baan van p
1 getekend met daarin de
knopenlijn (de blauwe lijn),
maar ditmaal zijn de
knopen
niet de plaatsen waar p
1
door het
eclipticavlak
gaat maar waar p
2 door het
baanvlak van p
1 gaat (dus
eigenlijk mag ik in dit geval de
knopenlijn
helemaal geen
knopenlijn noemen):
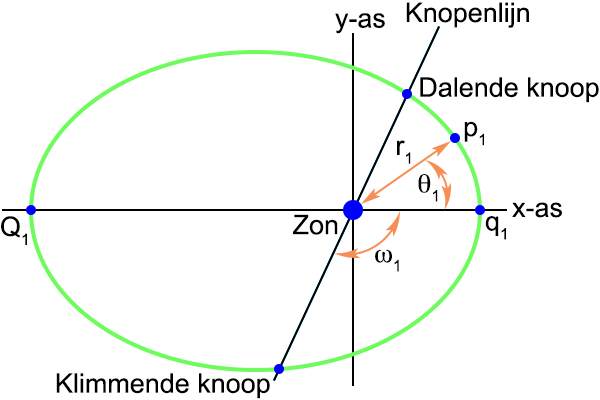
Figuur 3
Van deze
knopenlijn
maak ik een nieuwe X-as, en loodrecht daarop komt een nieuwe Y-as:

Figuur 4
Met de
apsidenlijn
als x-as kan ik voor r
1 schrijven:
Maar met de
knopenlijn
als X-as wordt dat:
De X-Y-Z-coördinaten van p
1 zijn dan:
Ik kan uiteraard ook de X-Y-Z-coördinaten van p
2 opschrijven.
De
baanvlakken
van p
1 en p
2 delen de X-as, want dat is immers de snijlijn van beide
baanvlakken.
Echter, het
baanvlak
van p
2 staat schuin onder een hoek i
21 ten opzichte van het
baanvlak van p
1 dus
daar moet ik even goed op letten:
In vergelijking (34a) zit het
inwendig product verstopt die mij
heel gemakkelijk leidt naar de
cosinus
van de hoek tussen r
1 en r
2:
En in vergelijking (34b) zit het
uitwendig product verstopt die mij
heel gemakkelijk leidt naar de
sinus
van de hoek tussen r
1 en r
2:
Ik ga wat extra constanten in het leven roepen:
Door (42b) te delen door (42a), en (42d) door (42c), kan ik c
12 en c
22 berekenen:
En (42a) en (42d) stellen mij daarna in staat om c
11 en c
21 te berekenen:
Hiermee kan ik de vergelijkingen (40) en (41) omschrijven als volgt:
Dit stoppen we vervolgens in de vergelijkingen (34):
Je vraagt je misschien af of ik wel bezig ben om naar een oplossing toe te werken, maar dat is toch echt wel het geval.
Sterker nog, we beginnen al redelijk in de buurt te komen.
Met behulp van (23b) en (23c) veranderen de vergelijkingen (45) in:
Ik heb in de teller nu nog maar één variabele (voor de eerste
integratie): E
2!
Voor de overzichtelijkheid haal ik er nog een stel hulpvariabelen bij:
Waarmee de vergelijkingen (46) een stuk overzichtelijker worden:
Nu moet ik nog met de noemer aan de slag.
Met behulp van de
cosinusregel kan ik voor
r
21 schrijven:
En met behulp van vergelijking (43) wordt dit:
De vergelijkingen (23) stellen mij in staat de volgende stap te maken:
Ik haal er nog maar een stel hulpvariabelen bij:
Waarmee (51) wordt:
Nu heb ik ook de noemer uitgedrukt in de variabele E
2.
Dit stop ik in de vergelijkingen (48):
En dit stop ik vervolgens in de
integralen
van de vergelijkingen (25):
Het zeer goede nieuws is dat beide
integralen
dezelfde noemer hebben!
Ik stel voor het gemak even:
Dan kan ik de
integralen I
1 en
I
2 als volgt schrijven:
Ik stel:
En dit stop ik allemaal weer terug in vergelijking (26):
De twee
integralen I
1 en I
2
zijn weer samengevoegd tot één
integraal!
Ik neem de teller daarvan apart en ik ga de haken wegwerken:
Dit vraagt gewoon om nog meer hulpvariabelen:
Hiermee kan ik (59) schrijven als volgt:
Nu hebben we weliswaar maar liefst vijf
integralen,
maar de oplossingen daarvan kunnen we allemaal vinden in de
tabel met integralen:
Het resultaat van de eerste keer
integreren wordt aldus:
Wat een zooitje hè, maar we hebben wel een exact antwoord!
Ik stel:
Hiermee wordt vergelijking (63):
En ik stel ook nog:
Hiermee wordt vergelijking (65):
De grootste horde is nu genomen, maar er rest nog een tweede
integraal.
Ik heb zojuist
geïntegreerd naar E
2 en nu
moet ik nog
integreren naar E
1.
Daarvoor zal ik mij moeten wenden tot een numerieke integratiemethode, want de variabele E
1 zit
inmiddels diep verweven in het bovenstaande tussenresultaat.
Dat is in dit geval helemaal niet erg, want ik hoef maar weinig integratieintervallen te berekenen om tot een
nauwkeurig antwoord te komen.
Zo wordt vergelijking (67):
Hierin is c
81-met-een-streepje-erboven de gemiddelde waarde van c
81 voor alle waarden van
E
1.
Nu ga ik nog even knutselen met die breuk met al die constanten die er voor staat.
Voor k' geldt (vergelijking (20) van de pagina
seculaire verstoringen):
En voor p
1 geldt (vergelijking (57) van de pagina
hemelmechanica):
Ik pak ook de
complementaire excentriciteit
er bij (vergelijking (77d) van de pagina
hemelmechanica):
En de
gemiddelde dagelijkse beweging
(vergelijking (82) van de pagina
hemelmechanica):
Dit ga ik allemaal invullen in die breuk van vergelijking (68) en die geef ik gelijk een naampje:
Waarmee vergelijking (68) uiteindelijk wordt:
Hier wil ik enkele opmerkingen over maken:
- Ik heb de
gemiddelde dagelijkse beweging
ingebracht in de constante K1, maar dat hoeft natuurlijk niet.
Ik kan K1 ook volledig uitdrukken in de
baanelementen van een planeet, maar
ergens moet een omrekening plaatsvinden van radialen per jaar naar boogseconden per tropische eeuw hier op Aarde
(periheliumprecessie
wordt doorgaans uitgedrukt in boogseconden per eeuw).
Dit zit allemaal ‘verstopt’ in de
gemiddelde dagelijkse
beweging.
- De complete
elliptische integralen
hebben als grenzen 0 en π/2 terwijl we over een hele planeetomloop willen
integreren, zijnde van 0 tot 2π, daarom
moet het uiteindelijke antwoord (vergelijking (74)) nog met vier vermenigvuldigd worden.
- Bovendien moet ik de berekening telkens opnieuw uitvoeren voor iedere verstorende planeet en alle resultaten
bij elkaar optellen.
Daarom is dit het lang gezochte resultaat:
Dus kunnen we dan nu eindelijk ‘echt’ gaan rekenen?
Nee, er is nog één akkefietje dat uitgezocht moet worden.
Want om te kunnen rekenen hebben we de
baanelementen nodig van de planeten:
- de halve lange baanas: a,
- de
numerieke excentriciteit,
of kortweg
excentriciteit: e,
- de
inclinatiehoek, of kortweg
inclinatie of
baanhelling: i,
- de hoek tussen de
klimmende knoop en het
perihelium, oftewel het
argument van het perihelium: ω,
- de hoek tussen het
lentepunt en de
klimmende knoop, oftewel de
lengte van de klimmende knoop: Ω,
- het tijdstip t waarvoor de bovenstaande vijf parameters gelden, de
epoche: t.
Echter, deze
baanelementen
worden allemaal gegeven ten opzichte van het
eclipticavlak, het vlak waar
de Zon en de Aarde in bewegen.
En omdat we voor dit specifieke probleem te maken hebben met Mercurius en een andere planeet zullen we twee
baanelementen moeten omrekenen:
Ik heb een plaatje gemaakt van de situatie:
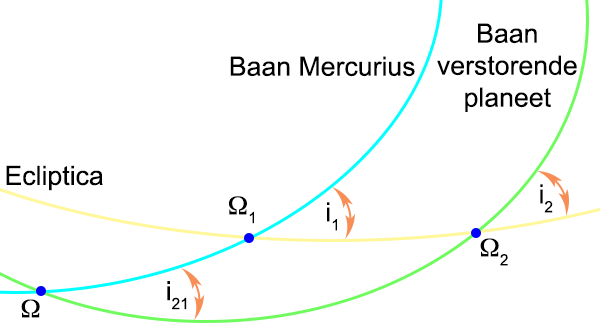
Figuur 5
Hierin is Ω
1 waar Mercurius door het
eclipticavlak gaat,
Ω
2 is waar de verstorende planeet door het
eclipticavlak gaat,
i
1 is de
inclinatiehoek
van het
baanvlak van Mercurius
ten opzichte van het
eclipticavlak
en i
2 is de
inclinatiehoek
van het
baanvlak van de verstorende planeet
ten opzichte van het
eclipticavlak.
Ik ga nu de
inclinatiehoeken
aan de andere kant van de
klimmende knopen
aangeven:
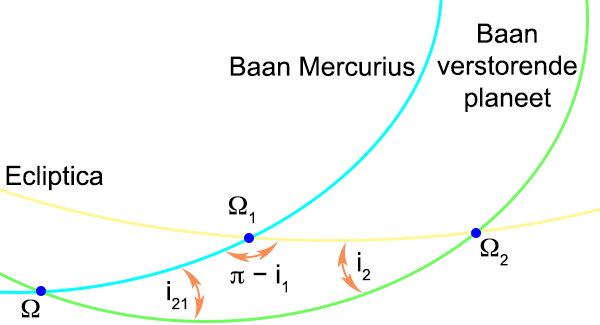
Figuur 6
De
klimmende knopen zijn hoeken
gemeten vanaf het
lentepunt.
Het verschil van beide is de hoek die ingesloten wordt door beide en die noem ik Ω
21:
En zo zijn er nog twee ingesloten hoeken, namelijk tussen de beide
klimmende knopen en de
klimmende knoop die beide
baanvlakken onderling maken, die noem
ik ε
1 en ε
2:
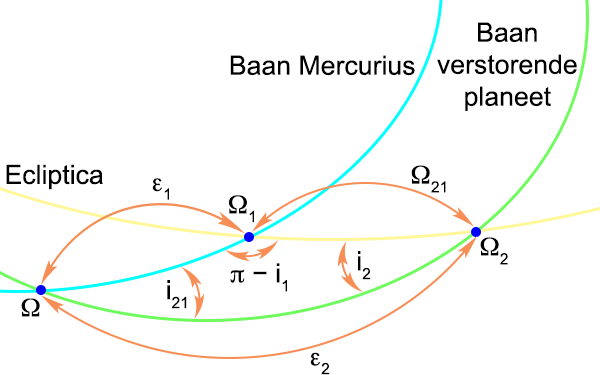
Figuur 7
Nu heb ik perfect een
boldriehoek
in kaart gebracht en hierop ga ik de
rekenregels voor de boldriehoek
toepassen.
Als eerste de
cosinusregel voor de hoeken:
En zo kom ik i
21 te weten.
Vervolgens pak ik de
sinusregel voor de boldriehoek
en die gebruik ik tweemaal om ε
1 en ε
2 te berekenen:
Verder weet ik dat de
argumenten van beide perihelia
gemeten zijn vanaf de
klimmende knopen
door het
eclipticavlak.
Gemeten vanaf de
onderlinge
knoop Ω geldt dan voor Mercurius
(want Ω is voor Mercurius de
klimmende knoop):
De
onderlinge knoop Ω
is voor de verstorende planeet echter de
dalende knoop.
Voor het
argument van het perihelium
van de verstorende planeet geldt daarom:
Tenslotte wil ik nog opmerken dat in tabellen met
baanelementen regelmatig in plaats van
het
argument van het perihelium
de
lengte van het perihelium
gegeven wordt.
Deze zijn in elkaar om te rekenen als volgt:
Nu kunnen we eindelijk echt gaan rekenen.
Hoe de berekening uit te voeren
- Afleiding van de vergelijkingen
- Hoe de berekening uit te voeren
- Berekeningen en resultaten
- Geschiedenis, conclusie en vooruitblik
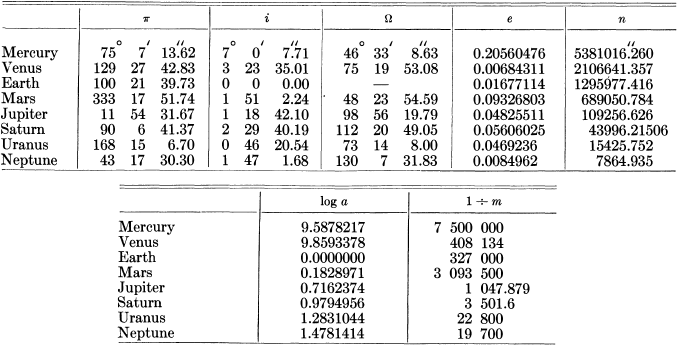
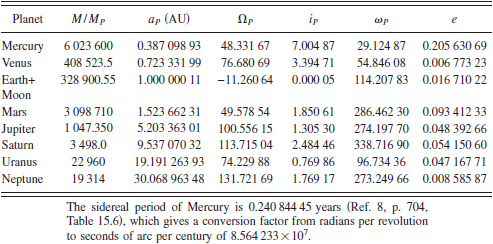
Allereerst zoeken we de gegevens op van de diverse planeten, per planeet hebben we de volgende
baanelementen nodig:
Nu ga ik de totale berekening doornemen voor Mercurius en één verstorende planeet.
Helemaal aan het einde tel ik dan de resultaten op voor alle planeten samen.
Bovendien moet ik onderstaande berekening doen voor iedere waarde van E
1, want de
integratie naar E
1 gaat via numerieke integratie,
oftewel via een reeks kleine stapjes (lees: allemaal verschillende waarden voor E
1 in een bepaald aantal
intervallen van 0 tot 360 graden).
Allereerst reken ik, indien nodig, de
lengte van het perihelium
om naar het
argument van het perihelium:
Daarna bereken ik p en de
complementaire excentriciteit
van beide planeten:
En tevens de verschilhoek tussen de beide
lengtes van de klimmende knoop:
Hiermee kan ik de onderlinge
inclinatiehoek berekenen:
Daarna bereken ik ε
1 en ε
2:
Hieruit volgt voor de
argumenten van de perihelia:
En die gaan vanaf nu verder door het leven als ω
1 en ω
2, dus zonder apostroph.
Nu kunnen c
12 en c
22 berekend worden:
En die dienen als opstapje naar c
11 en c
21:
Vervolgens bereken ik de afstand r
1:
En de
werkelijke anomalie
θ
1:
Dit maakt de weg vrij naar de berekening van de volgende variabelen:
En dat maakt op zijn beurt weer de weg vrij naar de berekening van deze variabelen:
Hetgeen ons brengt bij:
Nu duik ik in de uitwerking van de
integraal
en zoals gezegd vind je dat terug in de
tabel met integralen:
Hierbij geldt dat a = c
41, b = c
42, c = c
43, d = c
44 en e = 0.
Daar gaan we dan, om te beginnen normaliseer ik de noemer:
Daarmee kan ik de volgende stap maken:
En de volgende stap:
Zodat ik de volgende hoek kan uitrekenen:
Hiermee kan ik de nulpunten berekenen van de
derdegraads vergelijking
die ik onderweg tegenkom:
Daarmee kan ik de volgende variabelen berekenen:
Hetgeen mij in staat stelt om de variabelen α, β en γ en de diverse kruisproducten uit te rekenen:
En dat maakt de weg vrij naar deze variabelen:
Waarmee ik deze twee variabelen kan berekenen:
Dan zijn nu de
complete elliptische integraal van de tweede soort
en de
complete elliptische integraal van de eerste soort
aan de beurt volgens deze Taylor-reeksen:
Waaruit volgt:
En omdat:
Zo kom ik tenslotte bij:
Twee opmerkingen omtrent de berekeningen:
- in twee gevallen heb ik bij een hoek (een veelvoud van) π opgeteld of afgetrokken om in het
juiste kwadrant te blijven,
- de halve lange baanas is genormaliseerd naar astronomische eenheden (AE).
Dan kunnen we nu Excel aan het werk zetten.
Berekeningen en resultaten
- Afleiding van de vergelijkingen
- Hoe de berekening uit te voeren
- Berekeningen en resultaten
- Geschiedenis, conclusie en vooruitblik
Ik heb allereerst de berekeningen van Doolittle overgedaan met zijn gegevens:
Onderstaande tabel geeft de resultaten weer van Doolittle en mij:
 |
Doolittle |
De Vlieger |
Doolittle/De Vlieger |
| Venus |
277.636150000 |
277.634760890 |
1.000005003 |
| Aarde |
91.448833000 |
91.448814834 |
1.000000199 |
| Mars |
2.486334300 |
2.486334414 |
0.999999954 |
| Jupiter |
154.007200000 |
154.007183099 |
1.000000110 |
| Saturnus |
7.312262700 |
7.312266261 |
0.999999513 |
| Uranus |
0.142134790 |
0.142134469 |
1.000002262 |
| Neptunus |
0.041900885 |
0.041904488 |
0.999914019 |
| Totaal |
533.074815675 |
533.073398453 |
1.000002659 |
Tabel 1: periheliumprecessie van Mercurius
[boogseconden/eeuw] |
Zoals ik in het begin al vertelde hebben Hill en Doolittle zich in allerlei bochten gewrongen om deze berekening
te optimaliseren bij afwezigheid van computers.
Concreet betekent dit:
- ik heb de nulpunten van de
derdegraads vergelijking echt uitgerekend
terwijl Doolittle dit via een iteratieproces heeft gedaan,
- de tweede integratieslag werd door Doolittle gedaan met 8, 12 of 16 intervallen, terwijl ik standaard 48
intervallen heb gebruikt,
- respect voor Hill en Doolittle, het uiteindelijke resultaat uit 1912 wijkt minder dan drie-miljoenste af van
het moderne high-tech Excel-antwoord!
In 2005 verscheen een artikel van Melbourne Stewart, hij gebruikte een andere methode voor deze berekening
(namelijk via de Laplace-Runge-Lenz-vector).
Ik ga ook een vergelijking maken met zijn resultaten, maar helaas geeft Stewart zijn resultaten slechts met twee cijfers achter de komma.
Onderstaande tabel geeft de resultaten weer van Stewart en mij:
 |
Stewart |
De Vlieger |
Stewart/De Vlieger |
| Venus |
277.42 |
277.36 |
1.000216 |
| Aarde |
90.88 |
90.86 |
1.000220 |
| Mars |
2.48 |
2.48 |
1.000000 |
| Jupiter |
153.95 |
153.92 |
1.000195 |
| Saturnus |
7.32 |
7.32 |
1.000000 |
| Uranus |
0.14 |
0.14 |
1.000000 |
| Neptunus |
0.04 |
0.04 |
1.000000 |
| Totaal |
532.23 |
532.14 |
1.000169 |
Tabel 2:
periheliumprecessie van Mercurius
[boogseconden/eeuw] |
Ik was verbaasd dat mijn resultaten en die van Stewart niet beter met elkaar overeenstemmen (het scheelt weliswaar minder dan
0.2 promille, maar toch).
Het artikel van Stewart is uitermate summier en daarom gaf mij dat geen inzicht in de verklaring van het verschil.
Vervolgens heb ik meneer Stewart een email gestuurd in de hoop dat dat mij verder kon helpen.
Dit was zijn antwoord:
 |
 |
Dear de Vlieger,
I’m afraid I can’t be of much help in explaining why your calculation and my calculation agree to only 2 parts in 10,000.
I can’t redo the calculations since they were run (using Fortran) on an old computer that is no longer functional.
My best guess is that I just didn’t carry the calculations to the accuracy that you have done.
And I didn’t preserve the calculations in the very nice format that you have done in your manuscript.
I am sorry that I can’t be more definitive than that.
Sincerely,
Melbourne G Stewart
Professor of Physics Emeritus
Department of Physics
Wayne State University
Detroit, Michigan |
Beste de Vlieger,
Ik ben bang dat ik niet veel kan helpen in het verklaren waarom uw berekening en mijn berekening met elkaar overeenkomen
tot slechts 2 delen in 10000.
Ik kan de berekeningen niet overdoen, omdat ze uitgevoerd zijn (met gebruik van Fortran) op een oude computer die niet
langer in gebruik is.
Mijn beste inschatting is dat ik de berekeningen gewoon niet met die nauwkeurigheid heb uitgevoerd die u hebt gebruikt.
En ik heb de berekeningen niet bewaard in het hele overzichtelijke formaat dat u hebt gebruikt in uw verhaal.
Het spijt me dat ik niet eenduidiger kan zijn dan dit.
Hoogachtend,
Melbourne G Stewart
Professor of Physics Emeritus
Department of Physics
Wayne State University
Detroit, Michigan |
Geschiedenis, conclusie en vooruitblik
- Afleiding van de vergelijkingen
- Hoe de berekening uit te voeren
- Berekeningen en resultaten
- Geschiedenis, conclusie en vooruitblik
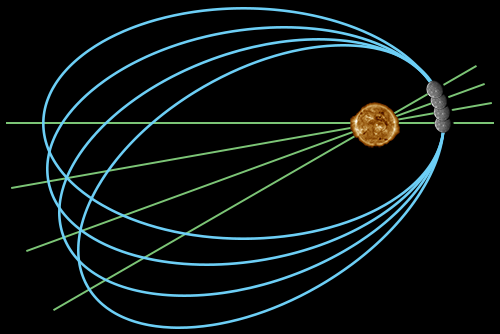
Het was de Fransman Urbain Le Verrier die in 1841 als eerste opmerkte dat er een afwijking zat in de baan van
de planeet Mercurius, een afwijking die men destijds (met de wetten van Newton) niet kon verklaren.
Er zat destijds ook een afwijking in de baan van de planeet Uranus en Le Verrier ging ook hieraan rekenen.
Hij ging ervan uit dat een nog onbekende planeet aan Uranus trok en berekende waar die planeet zich dan zou
moeten bevinden.
Toen hij daarmee klaar was werden deze coördinaten doorgegeven aan een sterrenwacht die dezelfde avond nog
de nieuwe planeet aantrof op (nagenoeg) de voorspelde positie.
Dit sterkte Le Verrier uiteraard in zijn overtuiging dat er bij Mercurius ook iets dergelijks aan de hand
moest zijn.
Hij rekende nog een aantal jaren stevig door en publiceerde in 1859 een uitgebreid artikel over
zijn werk waaruit ondubbelzinnig bleek dat de omloop van Mercurius niet klopte met de theorie: per eeuw
precesseerde Mercurius 38 boogseconden te veel.
Simpel gezegd: een Mercuriusjaar was ruim een halve seconde te vroeg afgelopen.
En een halve seconde is voor een wetenschapper genoeg om uuuuuuuuuuuren wakker van te liggen.
De Canadees Simon Newcomb doet het huiswerk van Le Verrier nog eens dunnetjes over en kan alleen maar
beamen dat de Fransman volkomen gelijk heeft.
En passant stelt hij het resultaat van Le Verrier bij van 38 naar 43 boogseconden per eeuw.
Er wordt druk gespeculeerd over een mogelijke oorzaak.
Le Verrier hypothetiseert in zijn artikel over een asteroïdengordel tussen Mercurius en de Zon
(“tels groupes d’astéroïdes existent aussi plus près du Soleil”) en in 1860 bezoekt hij een Franse
amateurastronoom die een planeetovergang (een planeet die vanaf de Aarde gezien voor de Zon langs trekt)
meent te hebben waargenomen.
De planeet krijgt prompt een naam, Vulcanus, maar de claim wordt nimmer bevestigd.
Tot zijn dood in 1877 blijft Le Verrier geloven in een bepaalde massa tussen Mercurius en de Zon die de
precessie zal verklaren.
Het is Albert Einstein die in 1915 met zijn
algemene relativiteitstheorie het precessieverschil
verklaart: kromming van de ruimtetijd veroorzaakt door de energie van de Zon.
Einstein leidt in zijn artikel de volgende vergelijking af (deze oplossing van Einstein is een
eerste orde benadering van het probleem, ik heb
ook de tweede orde benadering uitgerekend, maar
dat leverde geen significante extra term op):
Het sommetje dat je veel aantreft in boeken en op internet is het volgende:
gemeten precessie = Newton-precessie + Einstein-precessie
Of iets anders geformuleerd:
gemeten precessie = klassieke precessie + relativistische precessie
Vergelijking (81) is eenvoudig uit te rekenen en geeft als antwoord ε = 43 boogseconden per eeuw,
precies het onverklaarde precessiedeel!
Hiermee wordt het bovenstaande sommetje:
575 = 532 + 43
Deze uitleg, dit sommetje, kom je veel tegen en daarmee lijkt de kous af.
De
algemene relativiteitstheorie is bewezen en de baan van
Mercurius is verklaard, twee vliegen in één klap.
Toch houdt dit nog wel de gemoederen bezig, en wel om twee redenen:
- de klassieke precessie is zeer moeilijk uit te rekenen (zoals uit al het voorgaande mag blijken),
- de totale precessie is nog moeilijker te meten.
Waarschijnlijk omdat de precessie zo moeilijk is uit te rekenen, doet het merkwaardige feit zich voor dat
er in de geschiedenis van de mensheid meer mensen op de Maan hebben gelopen dan dat er mensen gerekend
hebben aan deze klassieke (niet-relativistische) precessie.
Wanneer je gaat zoeken op internet dan zul je ook merken dat er niet één webpagina is die in detail uit de
doeken doet hoe je deze precessie berekent.
Deze pagina, die je nu aan het lezen bent, is de eerste en tot nu toe de enige.
Even een historisch overzicht:
- 1841: Le Verrier berekent als eerste de klassieke precessie en stelt vast dat die niet overeenkomt
met de waarnemingen.
- 1859: Le Verrier heeft zijn berekeningen verfijnd/verbeterd en stelt het precessieverschil op
38 boogseconden per eeuw.
- 1895: Newcomb doet de berekeningen van Le Verrier over en stelt het precessieverschil bij
naar 43 boogseconden per eeuw.
- 1912: Doolittle berekent de precessie, maar met een andere methode (de
Gauss-integraal).
- 1915: Einstein verklaart met zijn algemene relativiteitstheorie
precies de 43 boogseconden per eeuw en de hele kwestie verdwijnt daarna uit de aandacht.
- 1947: Clemence publiceert een kort artikel met nieuwe precessiedata door uit te gaan van de berekeningen
van Doolittle en die aan te passen middels nieuwere/betere massagetallen van de diverse planeten
(wonderbaarlijk genoeg is het dit artikel waar
Wikipedia aan refereert
als bewijs voor de algemene relativiteitstheorie).
- 1979: Price en Rush publiceren een artikel met fundamentele fouten in de vergelijkingen die zij afleiden,
maar door puur toeval komen zij tot een goed antwoord.
- 2005: Stewart berekent de precessie (93 jaar na Doolittle!), maar met een andere methode
(de Laplace-Runge-Lenz-vector).
- 2017: De Vlieger berekent de precessie, weer met de
Gauss-integraal maar met de meest actuele
baanelementen en een hogere
nauwkeurigheid (door het gebruik van de computer).
De resultaten van al dit werk heb ik samengevat in onderstaande tabel:
 |

Le Verrier
(1841) |

Le Verrier
(1859) |

Newcomb
(1895) |

Doolittle
(1912) |

Clemence
(1947) |

Stewart
(2005) |

De Vlieger
(2017) |
| Venus |
287.00 |
280.60 |
|
277.64 |
277.86 |
277.42 |
277.36 |
| Aarde |
86.00 |
83.60 |
|
91.45 |
90.04 |
90.88 |
90.86 |
| Mars |
3.00 |
2.60 |
|
2.49 |
2.54 |
2.48 |
2.48 |
| Jupiter |
158.00 |
152.60 |
|
154.01 |
153.58 |
153.95 |
153.92 |
| Saturnus |
8.00 |
7.20 |
|
7.31 |
7.30 |
7.32 |
7.32 |
| Uranus |
|
0.10 |
|
0.14 |
0.14 |
0.14 |
0.14 |
| Neptunus |
|
|
|
0.04 |
0.04 |
0.04 |
0.04 |
| Totaal |
542.00 |
526.70 |
532.55 |
533.07 |
531.50 |
532.23 |
532.14 |
Tabel 3: overzicht berekende klassieke
periheliumprecessie van Mercurius
[boogseconden/eeuw] |

Echter, een ketting is zo sterk als zijn zwakste schakel.
Want het resultaat van bijna twee eeuwen rekenen-aan-Mercurius staat hierboven in een tabel die op een half
A4-tje past.
Dat is bijzonder mager.
Daar komt bovenop dat meetresultaten van de precessie van Mercurius nog veel schaarser zijn (net zoals je
op internet geen details vindt betreffende de berekening van de klassieke precessie, vind je daar ook geen
meetresultaten).
Op internet is er alleen maar een vicieuze cirkel van citeren en geciteerd worden met het inmiddels overbekende
rijtje 575 - 532 - 43.
Als je gaat opzoeken waar de 575 en de 532 werkelijk vandaan komen wordt het oorverdovend stil.
In de wetenschappelijke literatuur is het niet beter, want voor zover ik kan nagaan is er na Le Verrier één keer
gemeten aan de precessie van Mercurius (door Shapiro) en iedereen refereert aan dat resultaat (en ik heb best
wel wat boeken aangaande dit onderwerp).

BepiColombo onderweg naar Mercurius
(Credits: ESA)
In 2018 wordt BepiColombo gelanceerd die in 2025 bij Mercurius zal arriveren.
ESA schrijft hierover het volgende op haar website:
“It will set off in 2018 on a journey to the smallest and least explored terrestrial planet in our Solar System.
An ambitious, multi-spacecraft mission to explore the planet Mercury in unprecedented detail is now scheduled
for lift-off from Europe’s spaceport at Kourou, French Guiana, in October 2018.”
Ik twijfel er niet aan dat BepiColombo een eersteklas positiebepaler aan boord heeft.
Kortom, wetenschap blijft altijd spannend.
Weten we over tien jaar eindelijk het exacte antwoord op het Mercuriusprobleem?

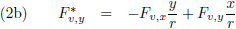
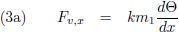
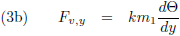
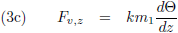
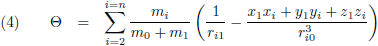
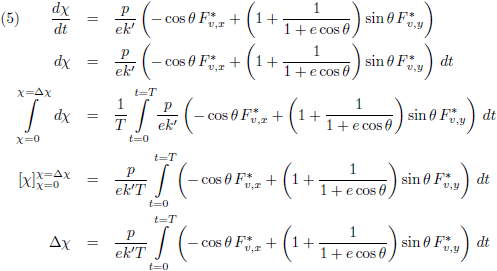
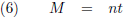
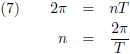
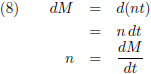
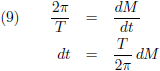
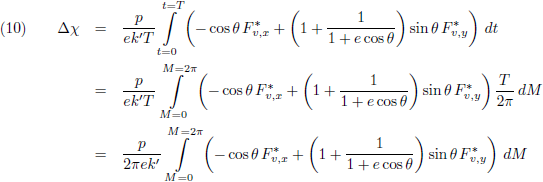
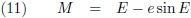
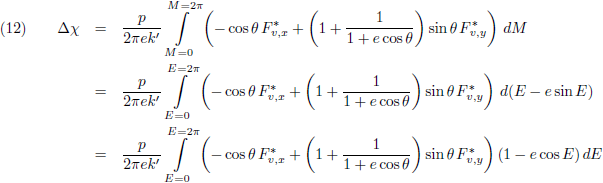
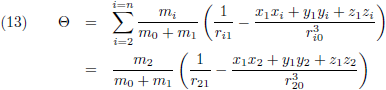
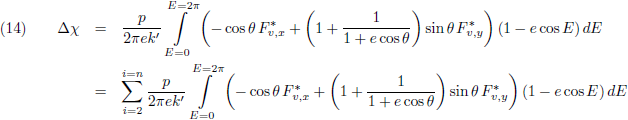
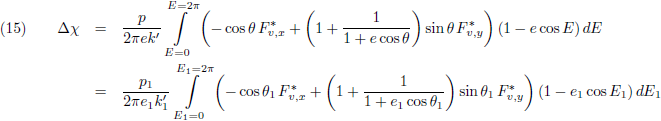
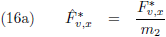
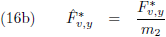
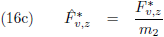
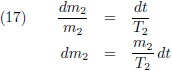
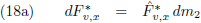
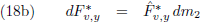
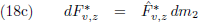
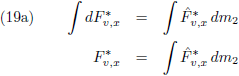
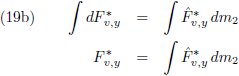
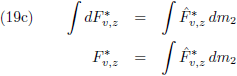
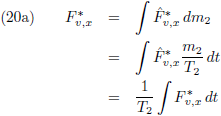
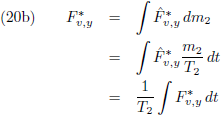
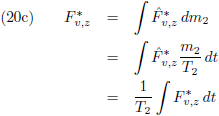
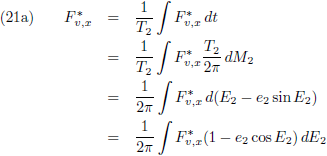
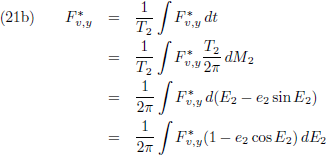
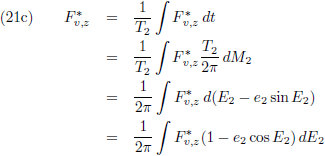
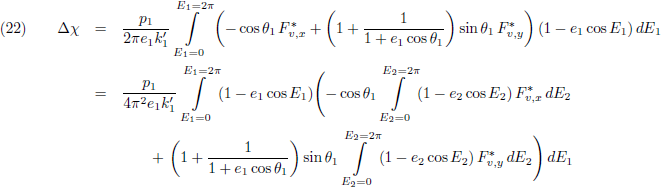
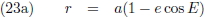
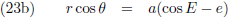
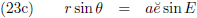
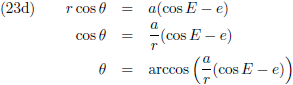
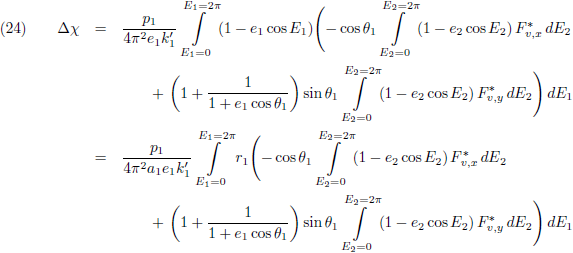
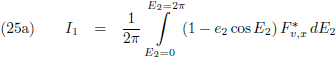
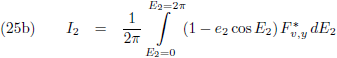
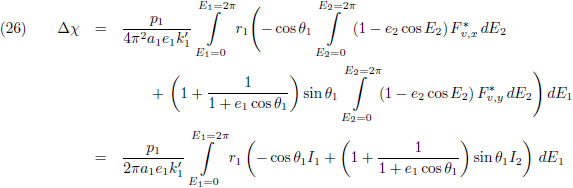
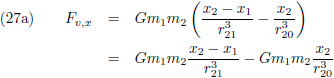
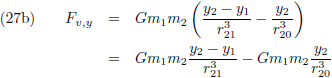
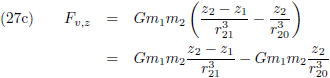
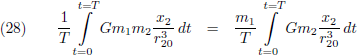
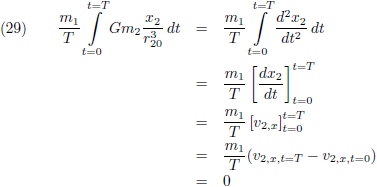
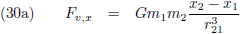
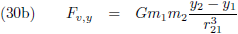
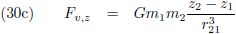

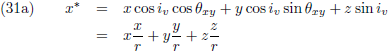
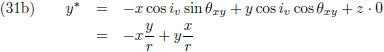
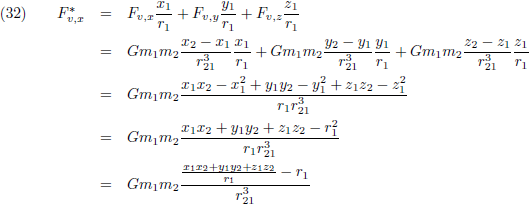
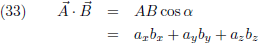
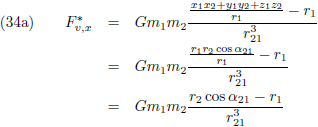
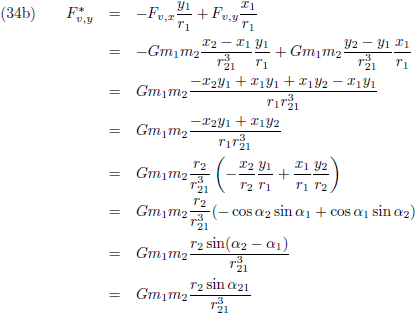
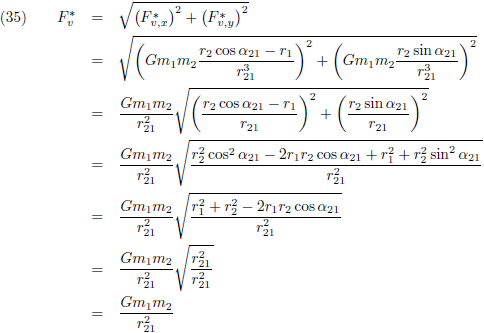


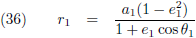
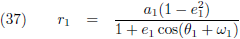
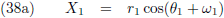
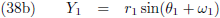
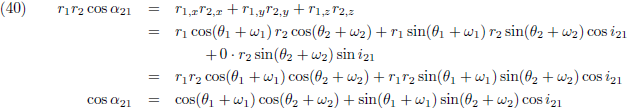
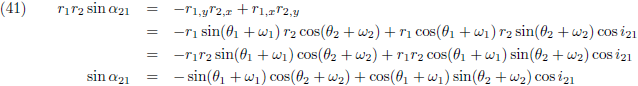
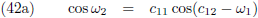

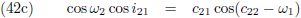
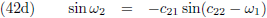


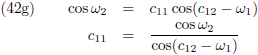
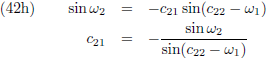
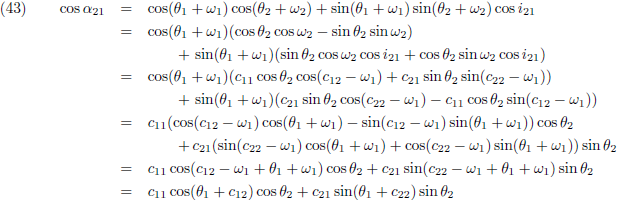
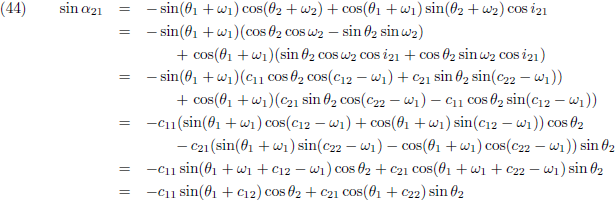
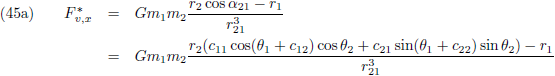
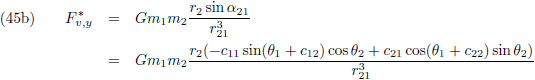
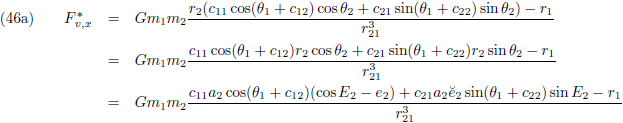
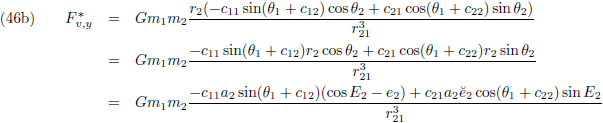
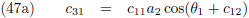
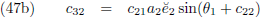
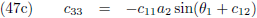
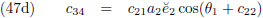
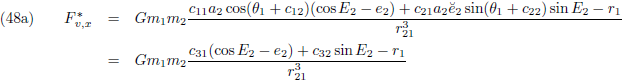
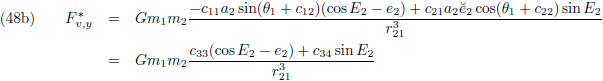
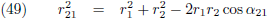
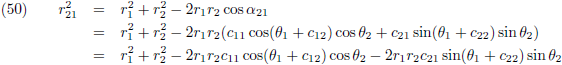
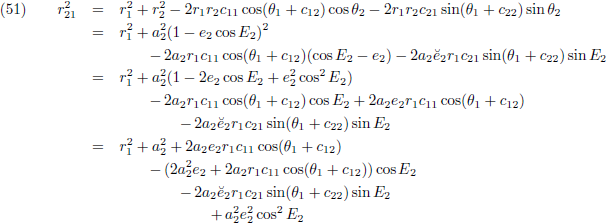
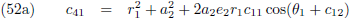
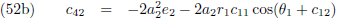
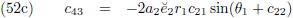
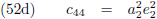
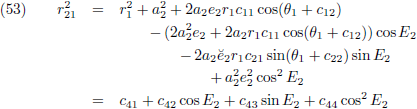
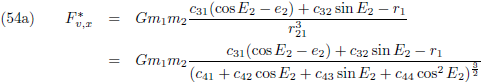
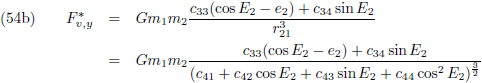
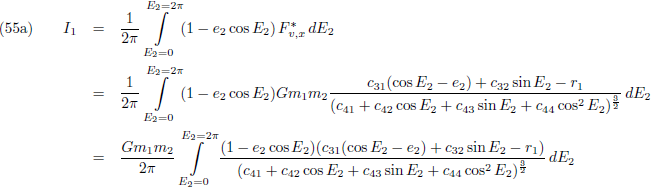
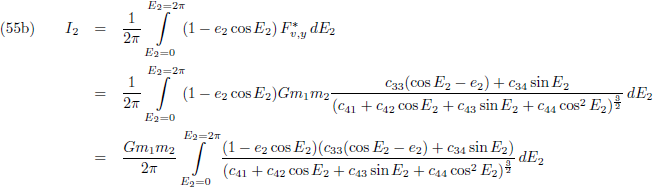
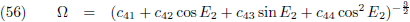
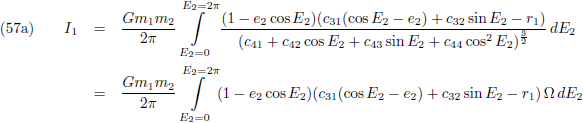
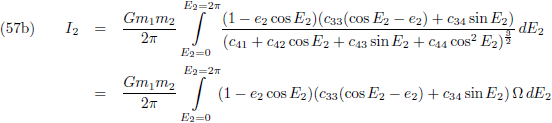
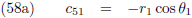
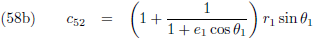

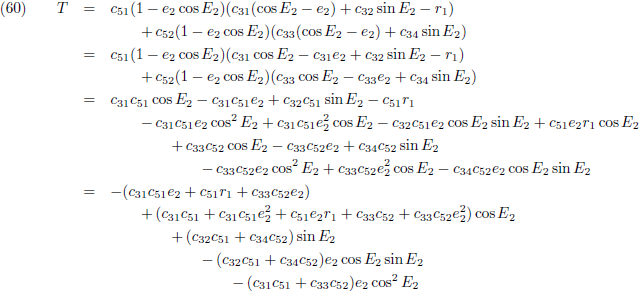
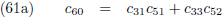
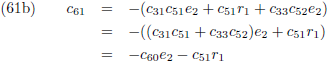
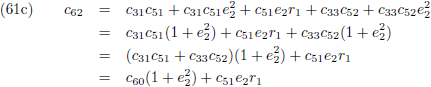
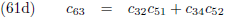
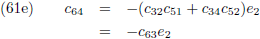
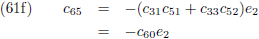
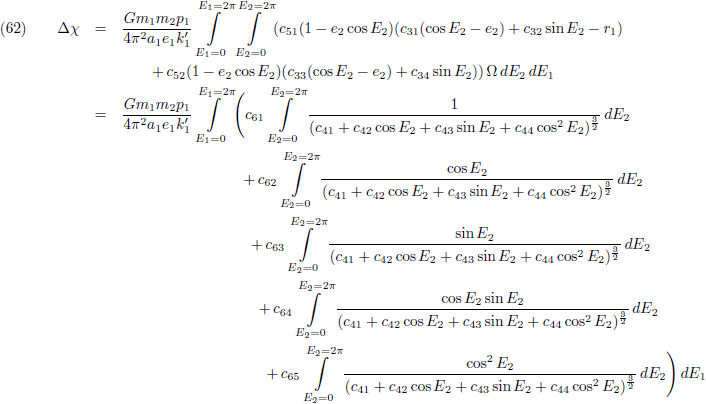
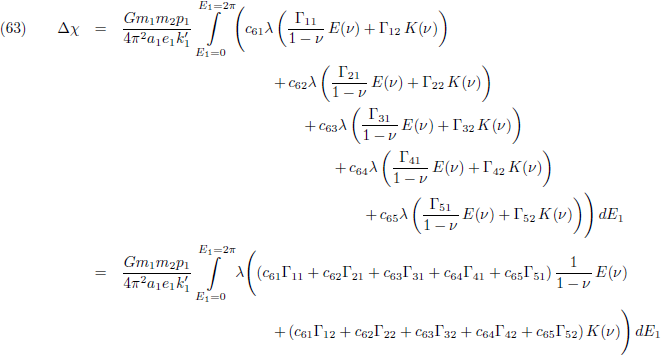
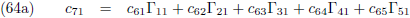
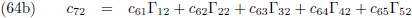
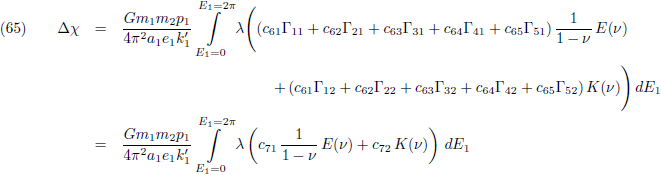
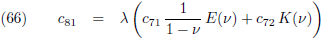
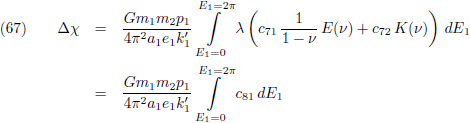
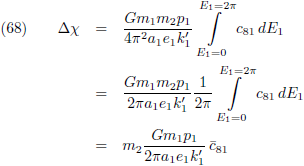
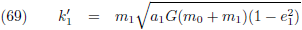
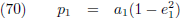
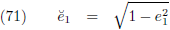
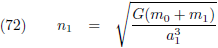
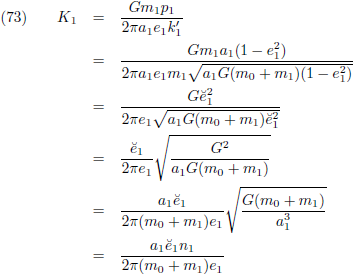
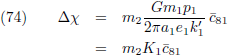
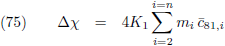




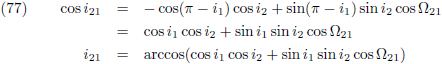
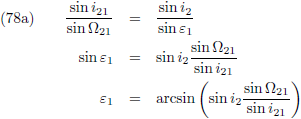
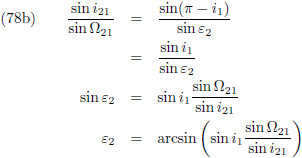
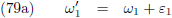

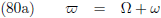
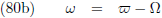
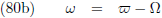
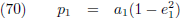
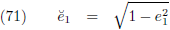

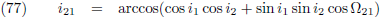
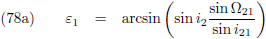
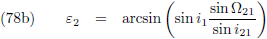
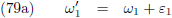

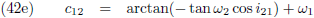
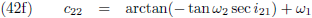
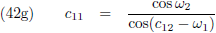
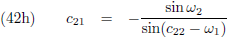
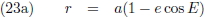
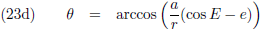
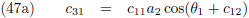
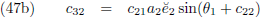
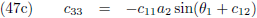
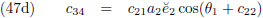
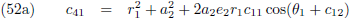
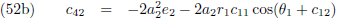
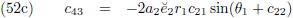
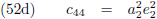
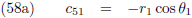
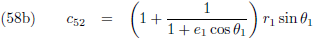
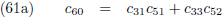
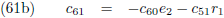
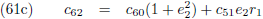
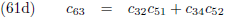
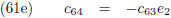
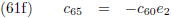

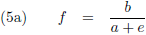
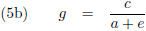
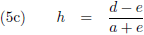
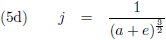

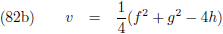
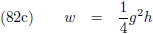
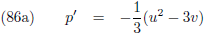
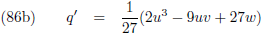
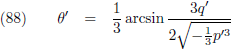
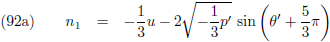
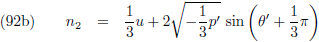

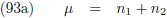
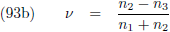
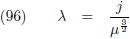
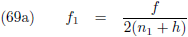
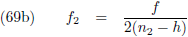
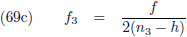

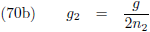
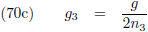
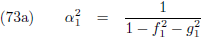
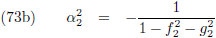
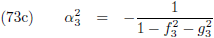
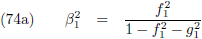
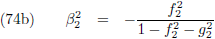
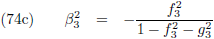
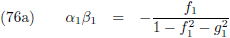
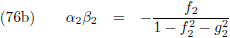
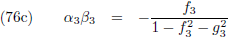
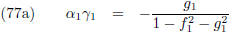
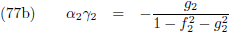
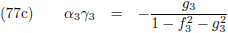
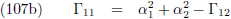
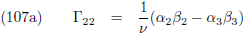
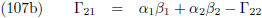
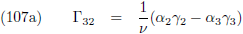
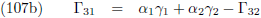
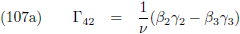
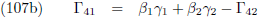
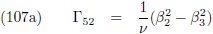
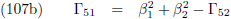
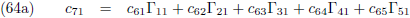
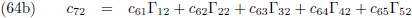
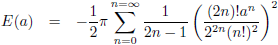
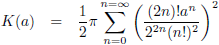
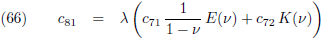
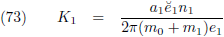
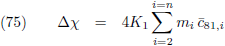




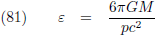
















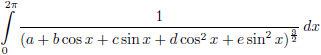
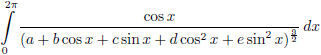
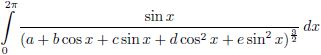
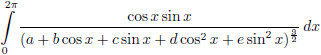
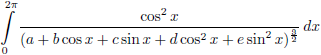









 Door naar het volgende vraagstuk: het traagheidsmoment van een homogene ronde ster
Door naar het volgende vraagstuk: het traagheidsmoment van een homogene ronde ster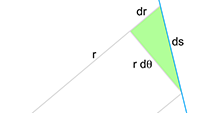 Terug naar het vorige vraagstuk: de wetten van Kepler met niet-verwaarloosbare secundaire massa
Terug naar het vorige vraagstuk: de wetten van Kepler met niet-verwaarloosbare secundaire massa Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina astronomie
Naar de overzichtspagina astronomie Periheliumprecessie als gevolg van een oblate ster
Periheliumprecessie als gevolg van een oblate ster Relativistische periheliumprecessie, 1e orde benadering
Relativistische periheliumprecessie, 1e orde benadering Relativistische periheliumprecessie, 2e orde benadering
Relativistische periheliumprecessie, 2e orde benadering Seculaire verstoringen
Seculaire verstoringen De reis naar de werkelijkheid van Barack Obama
De reis naar de werkelijkheid van Barack Obama De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 18
Vectoren, vraagstuk 18 Vectoren, vraagstuk 56
Vectoren, vraagstuk 56 Vectoren, vraagstuk 94
Vectoren, vraagstuk 94 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 1: snelheden
Relativiteitstheorie basic, hoofdstuk 1: snelheden Uitleg artikel algemene relativiteitstheorie: paragraaf 16
Uitleg artikel algemene relativiteitstheorie: paragraaf 16 De relativistische bewegingsvergelijkingen
De relativistische bewegingsvergelijkingen Leid de energie-impuls-relatie af
Leid de energie-impuls-relatie af Het modelleren van de dichtheid van de Zon
Het modelleren van de dichtheid van de Zon Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen