Klassieke afleiding van de formule van Heaviside
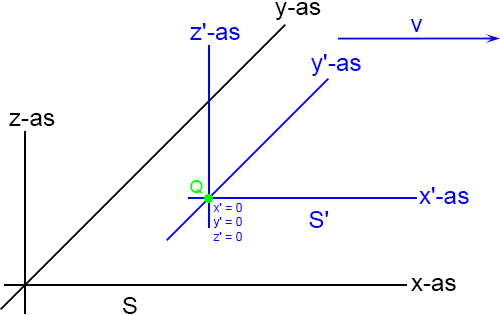
Ik begin met de wet van De Coulomb voor het elektrische veld van een lading Q (die feitelijk geldt ‘in rust’, of beter gezegd: voor een waarnemer die met de lading Q meebeweegt):
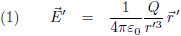
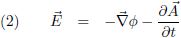
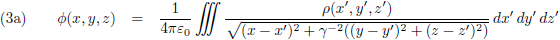
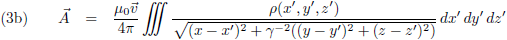
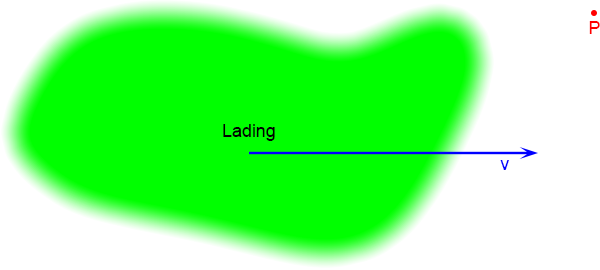
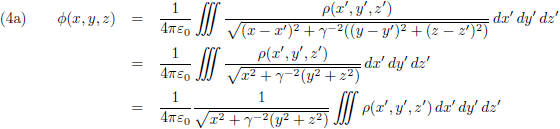
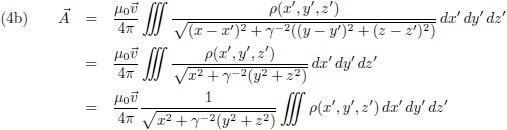
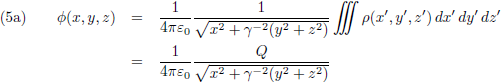
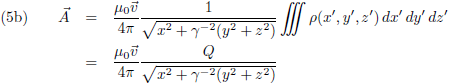
Deze potentialen ga ik invullen in vergelijking (2), maar voordat ik dat doe herinner ik mijzelf er aan dat de Lorentz-ijk gevolgen had voor de afgeleiden:
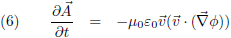
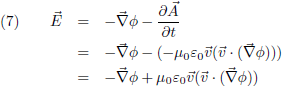

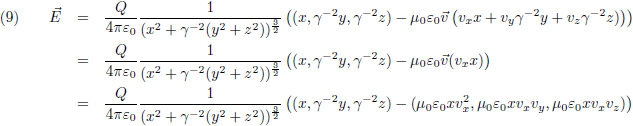
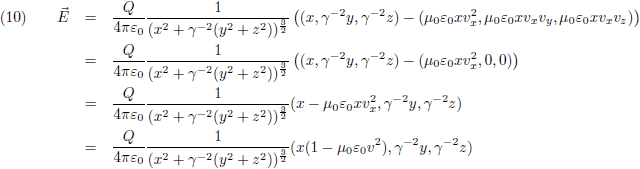
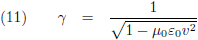
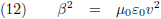
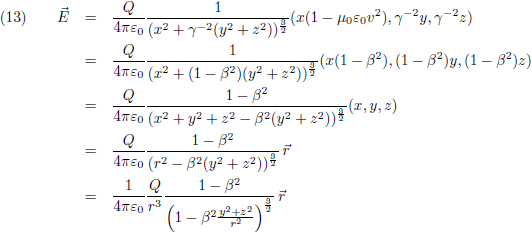
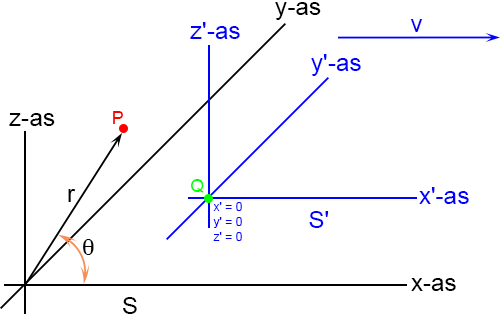
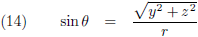
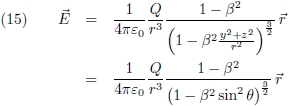
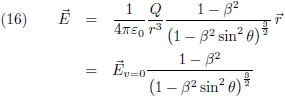
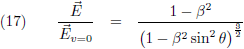
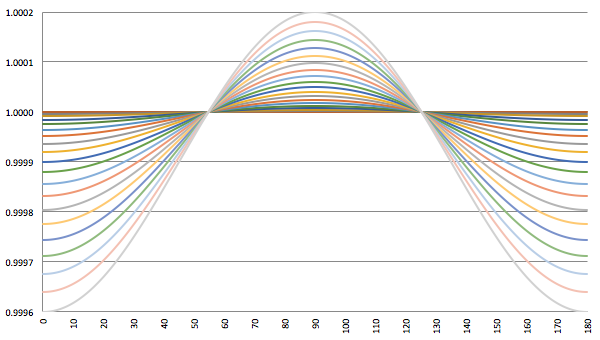
Vergelijking (17) is de gezochte formule van Heaviside. Ik maak hier even een plaatje van, horizontaal is θ uitgezet (van 0 tot 180 graden) en ik laat β in stapjes van 0.001 oplopen tot 0.02 (= 6000 km/s!). Je ziet dat de functie dan amper afwijkt van één:
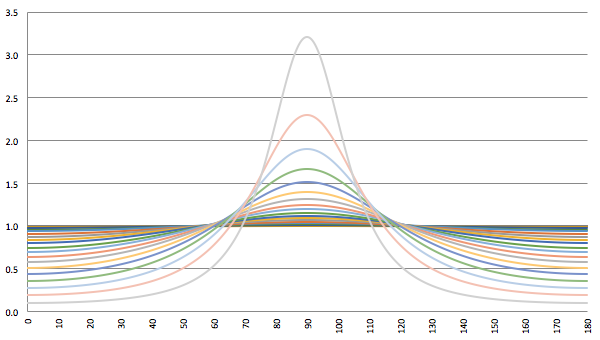
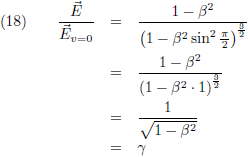
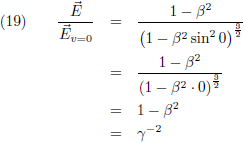
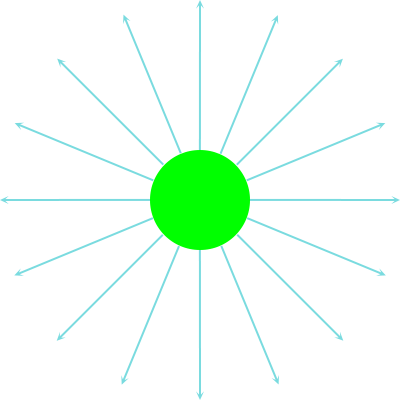
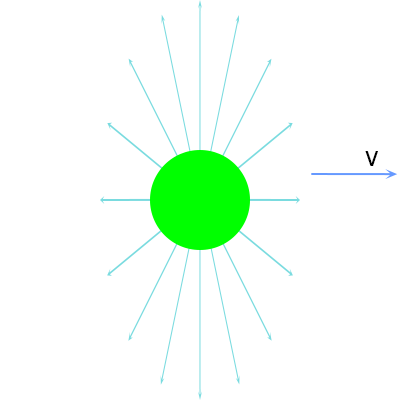
Merk ook op dat ik deze afleiding, om tot de formule van Heaviside te komen, gedaan heb zonder ook maar iets te zeggen over inertiaalstelsels of de ether of wat voor relativistische principes dan ook. Dat Moeder Natuur zoiets als het fenomeen invariantie bedacht had was anderhalve eeuw geleden nog ondenkbaar en daar heb ik dan ook niet aan gerefereerd. Het woord “lichtsnelheid” is niet gevallen, noch heb ik het symbool “c” gebruikt. Ik heb ook geen golfvergelijkingen gebruikt, laat staan opgelost (waar dan de lichtsnelheid uit naar voren was gekomen). Ik heb alleen de wetten van Maxwell gebruikt, elektromagnetische potentialen in het leven geroepen en verder alleen maar wiskunde bedreven. Dat was immers ook het enige gereedschap dat Heaviside destijds (in de jaren tachtig van de negentiende eeuw) tot zijn beschikking had.
Heaviside kwam met zijn formule ruim twintig jaar voordat Einstein zijn speciale relativiteitstheorie publiceerde, oftewel Heaviside had nog helemaal geen beschikking over relativistische vergelijkingen en werkte met alleen maar klassieke elektromagnetische wetten (de wetten van Maxwell) naar zijn formule toe. Een opmerkelijk resultaat! De formule van Heaviside is ook af te leiden vanuit de speciale relativiteitstheorie en dan weer te beginnen bij de wet van De Coulomb en vervolgens alle relativistische transformatievergelijkingen (die de invariantie van de lichtsnelheid als uitgangspunt hebben) in te zetten. Hoe dat precies in zijn werk gaat vind je op deze pagina.





 Door naar het volgende vraagstuk: 1 gram elektronen in een kistje
Door naar het volgende vraagstuk: 1 gram elektronen in een kistje Terug naar het vorige vraagstuk: oplossing voor de elektromagnetische potentialen
Terug naar het vorige vraagstuk: oplossing voor de elektromagnetische potentialen Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina elektriciteit en magnetisme
Naar de overzichtspagina elektriciteit en magnetisme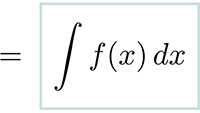 Integreren
Integreren Differentiëren
Differentiëren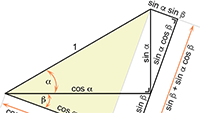 Goniometrie in het platte vlak
Goniometrie in het platte vlak Wat is een vector?
Wat is een vector?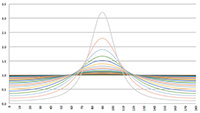 Relativistische afleiding van de formule van Heaviside
Relativistische afleiding van de formule van Heaviside De potentialen van het elektromagnetische veld
De potentialen van het elektromagnetische veld Een geodetische lijn rondom een puntmassa
Een geodetische lijn rondom een puntmassa De illusie van zekerheid
De illusie van zekerheid Volgen, achtervolgen, vervolgen en de gevolgen
Volgen, achtervolgen, vervolgen en de gevolgen De integraal van
De integraal van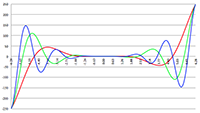 De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van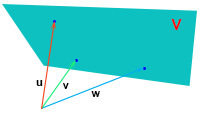 Vectoren, vraagstuk 8
Vectoren, vraagstuk 8 Vectoren, vraagstuk 46
Vectoren, vraagstuk 46 Vectoren, vraagstuk 84
Vectoren, vraagstuk 84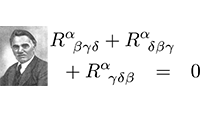 De Bianchi-identiteit
De Bianchi-identiteit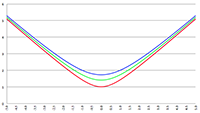 De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van De faculteitsfunctie
De faculteitsfunctie Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen