Ruimtetijdkromming
Iedereen zegt wel zo gemakkelijk “zwaartekracht is ruimtetijdkromming”, maar wanneer ik iets laat vallen dan valt dat ‘iets’
gewoon recht naar beneden.
Waar zit dan die ruimtetijdkromming, hoe manifesteert die zich?
Stel ik heb een balletje in de hand en die gooi ik weg, omhoog om precies te zijn.
Het balletje verlaat mijn hand op een hoogte van één meter, bereikt kort daarna een hoogste punt van twee meter en komt
uiteindelijk op een afstand van drie meter van mijn hand op de grond terecht.
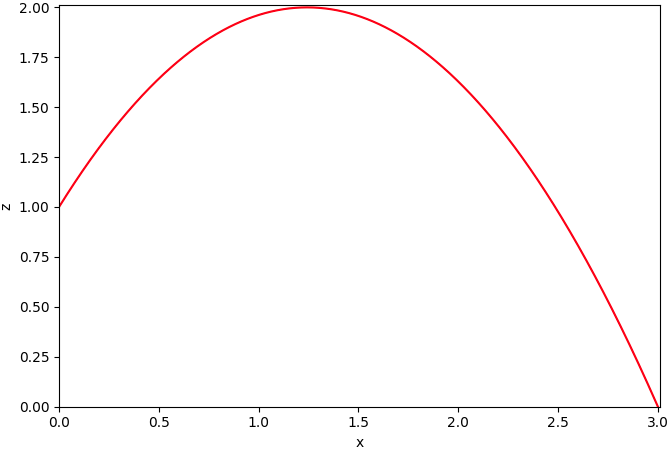
Ik maak daar even een plaatje van en de horizontale afstand noem ik x en de verticale afstand z.
Vervolgens laat ik het plaatje ‘voorover vallen’, de verticale afstand z is nu naar voren gericht en er ontstaat in de grafiek
ruimte voor een derde dimensie.
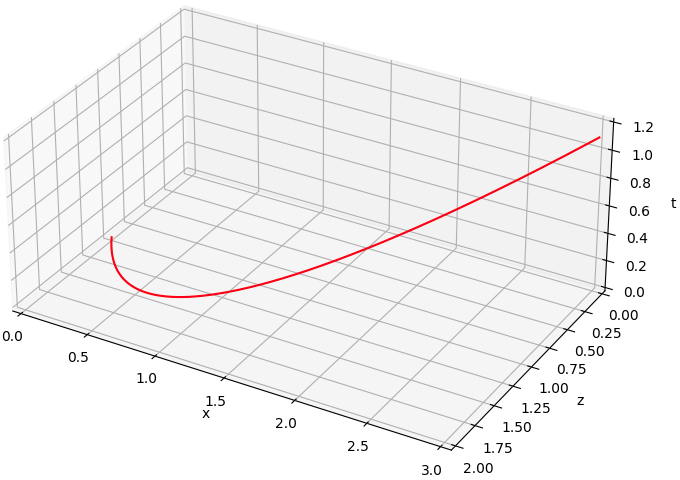
Deze derde dimensie wordt de tijd.
Terwijl het balletje zich voortbeweegt in de x-dimensie en de z-dimensie verstrijkt er natuurlijk ook tijd.
Die ga ik er nu bij inbrengen.
Enig rekenwerk vertelt mij dat het balletje bijna 1.1 seconde nodig heeft voor het totale traject (waarbij ik de luchtweerstand
verwaarloos).
Zo beweegt het balletje in de ruimtetijd.
Er ontbreekt één ruimtelijke dimensie, de y-dimensie, maar die heb ik toch niet nodig voor dit probleem en zo blijft het plaatje
maakbaar (een driedimensionaal plaatje maken lukt nog, een vierdimensionaal plaatje niet).
Het bovenstaande plaatje heeft wel een probleem, want ik ben appels met peren aan het vergelijken.
De x-dimensie en de z-dimensie staan uitgezet in meters en de t-dimensie in seconden en dat zal ik gelijk moeten trekken.
Hét recept om tijd om te zetten naar meters is vermenigvuldigen met de lichtsnelheid c, dus dat ga ik doen voor het volgende
plaatje waarbij ik in eerste instantie c = 1 m/s stel.
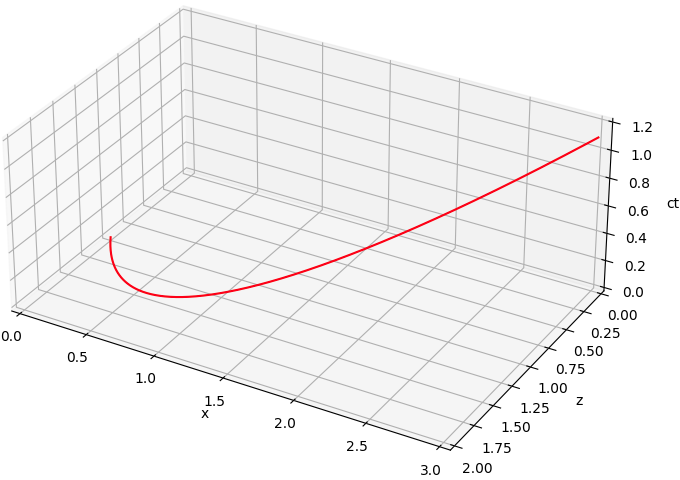
Bij de verticale as staat nu ct in plaats van t, maar verder is het plaatje identiek aan het vorige.
Het belangrijke verschil is wel dat nu alle assen meters aangeven.
Het bovenstaande plaatje is gemaakt met c = 1 m/s, maar dat is zeer ver verwijderd van de werkelijke waarde.
Ik ga c in stapjes verhogen om te laten zien wat er dan gebeurt, ik stel nu dat c = 10 m/s.
Van de oorspronkelijke parabool is nu al weinig meer te herkennen.
Voor het volgende plaatje stel ik dat c = 100 m/s.
Van een fatsoenlijke grafiek is nu al helemaal niets meer over en toch ga ik c nogmaals verhogen, ditmaal stel ik c = 1000 m/s.
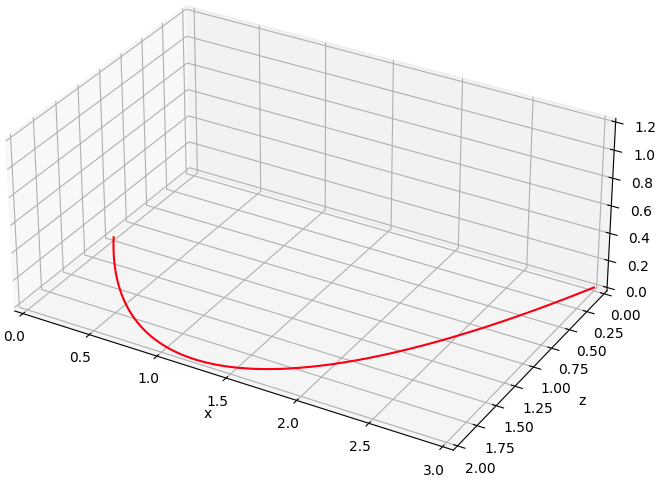
De parabool waar ik in het eerste plaatje mee begon, bezien in twee
ruimtelijke dimensies (x en z), blijkt bezien in de
ruimtetijd nagenoeg een rechte lijn.
En dat terwijl ik in het bovenstaande plaatje c = 1000 m/s had gesteld, terwijl de werkelijke waarde c = 299792458 m/s is, bijna
een factor driehonderdduizend hoger.
In de ruimtetijd volgt het balletje een bijna perfecte rechte lijn, de kortste verbinding tussen twee punten.
Ik kan dit ook op een andere manier laten zien door opnieuw een tweedimensionaal plaatje te maken, net als het eerste plaatje,
waarbij ik de x-dimensie weglaat en z uitzet tegen de tijd (vermenigvuldigd met c om weer op meters uit te komen, en ik stel
eerst weer c = 1 m/s).
Ik ga c weer in stappen verhogen, voor het volgende plaatje stel ik c = 10 m/s.
Vervolgens stel ik c = 100 m/s.
En tenslotte stel ik ook nog c = 1000 m/s.
Je ziet het al aankomen, ook vanuit dit perspectief volgt het balletje een bijna perfecte rechte lijn.
Met de nadruk op
bijna, want ofschoon het balletje slechts 1.1 seconde nodig heeft voor het gehele traject is dat uitgedrukt
in meters bijna 327 miljoen meters (vermenigvuldigen met de lichtsnelheid c = 299792458 m/s)!
De afwijking van een perfecte rechte lijn is de afwijking in de z-dimensie en die is het gevolg van de kromming van de ruimtetijd.
Deze kromming ontstaat door de energie van de Aarde, want energie genereert ruimtetijdkromming, en die kromming ervaren wij in ons
dagelijks leven als zwaartekracht.
Maar hoe zit dat dan wanneer je iets ‘gewoon’ laat vallen?
Want tot nu toe had ik het over een balletje dat ik omhoog gooi, terwijl de oorspronkelijke vraag erover ging waar de ruimtetijdkromming
‘zit’ wanneer je iets simpelweg laat vallen.
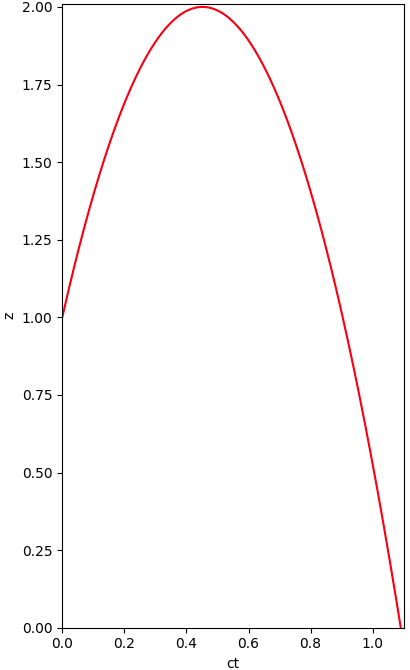
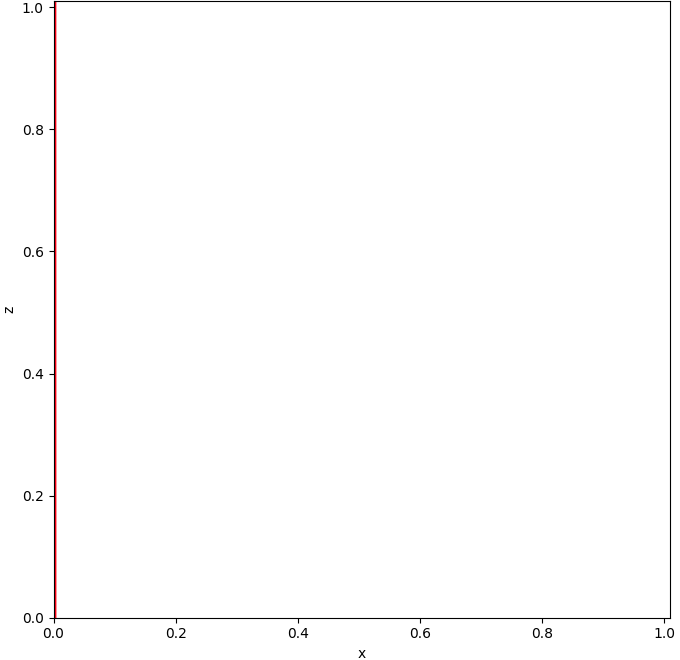
In een plaatje met twee ruimtelijke dimensies ziet dat er zo uit, het balletje valt van een meter hoogte op de grond zonder
enige beweging in de x-dimensie.
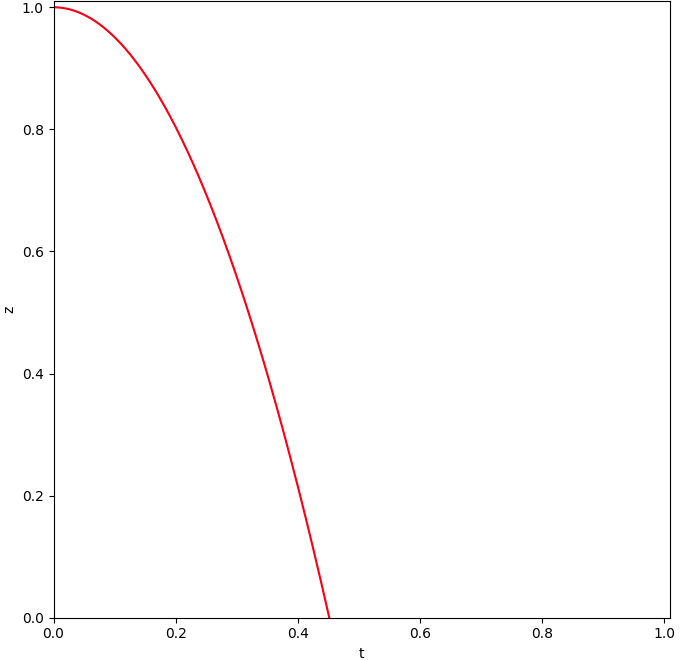
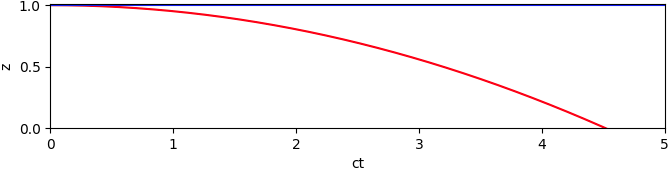
De hoogte van het balletje als functie van de tijd ziet er een stuk interessanter uit, na iets meer dan 0.45 seconde raakt het
balletje de grond.
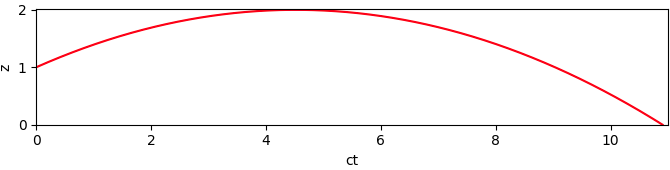
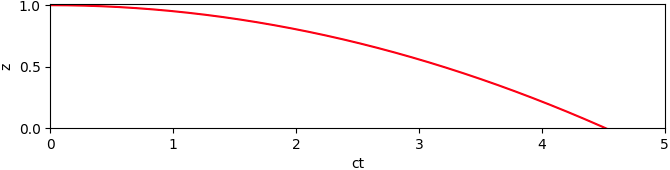
De procedure is inmiddels bekend, door de tijd met de lichtsnelheid c te vermenigvuldigen zetten we seconden om in meters.
Ik begin met c = 10 m/s.
Vervolgens stel ik c = 100 m/s.
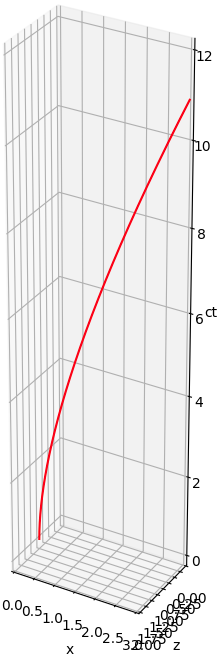
En tenslotte stel ik ook nog c = 1000 m/s.
Ook op deze manier ontstaat hetzelfde beeld: het balletje volgt een bijna perfecte rechte lijn.
Terwijl het balletje een meter afbuigt in de z-dimensie legt datzelfde balletje ruim 135 miljoen meters af in de tijdsdimensie.
De afwijking van een perfecte rechte lijn is de afwijking in de z-dimensie en die is één meter, en die minimale afwijking van
één op 135 miljoen is het gevolg van de kromming van de ruimtetijd.
Merk tenslotte op dat in de laatste plaatjes de x-dimensie helemaal niet meer voorkomt, dus of ik het balletje weggooi (hetgeen zorgt
voor verplaatsing in de x-dimensie) of simpelweg laat vallen (geen verplaatsing in de x-dimensie) maakt helemaal niets uit.
De ruimtetijdkromming manifesteert zich alleen in de z-dimensie, dus verticaal, en dat is ook de enige richting waarin wij in ons
dagelijks leven de zwaartekracht voelen.
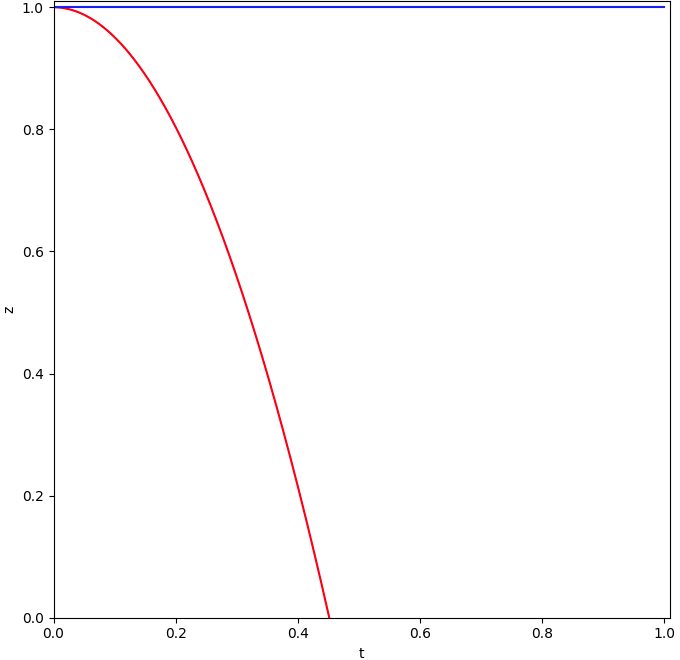
Indien er geen zwaartekracht zou zijn, dan zou het balletje ook niet vallen, de blauwe lijn in het plaatje hieronder.
Ik zal de horizontale as, de tijd, weer even omrekenen naar meters, ditmaal alleen met c = 10 m/s (want je hebt inmiddels wel door
wat er gebeurt wanneer ik hogere waarden voor c gebruik).
Het verschil tussen de blauwe lijn en de rode lijn is de kromming van de ruimtetijd aan het oppervlak van de Aarde: één ‘verticale’
meter per meer dan 135 miljoen ‘tijdmeters’.




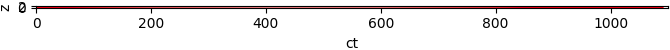


 Door naar het volgende vraagstuk: de uitdijing van het heelal
Door naar het volgende vraagstuk: de uitdijing van het heelal Terug naar het vorige vraagstuk: leid de energie-impuls-relatie af
Terug naar het vorige vraagstuk: leid de energie-impuls-relatie af Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van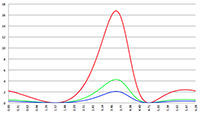 De integraal van
De integraal van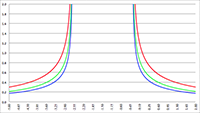 De integraal van
De integraal van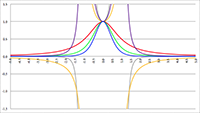 De integralen van
De integralen van Vectoren, vraagstuk 59
Vectoren, vraagstuk 59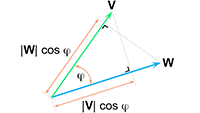 Invariantie van het inwendig product
Invariantie van het inwendig product Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 4: de zaklamp
Relativiteitstheorie basic, hoofdstuk 4: de zaklamp Uitleg artikel algemene relativiteitstheorie: inleiding hoofdstuk D
Uitleg artikel algemene relativiteitstheorie: inleiding hoofdstuk D Wat is geodetisch?
Wat is geodetisch? De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt Kwantummechanica
Kwantummechanica Afleiding van de algemene golfvergelijking
Afleiding van de algemene golfvergelijking De illusie van ons onderwijssysteem
De illusie van ons onderwijssysteem De reis naar de werkelijkheid van Anky van Grunsven
De reis naar de werkelijkheid van Anky van Grunsven De djembé
De djembé De Natuur spreekt: The Soil/De Grond
De Natuur spreekt: The Soil/De Grond Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen