Afleiding van de algemene golfvergelijking
Leid de algemene golfvergelijking af.
Stel ik heb een touw, en dat touw is aan beide uiteinden vastgebonden.
Ik zorg dat het touw flink strak staat en daardoor werkt er een kracht op het touw (lees: in het touw) ter grootte van F.
Vervolgens pak ik het touw ergens vast, ik geef het een uitwijking in verticale richting en vervolgens laat ik het weer los.
De verticale uitwijking zal zich nu in horizontale richting door het touw gaan verplaatsen, als golfbeweging, en dat aspect
gaan we nader onderzoeken.
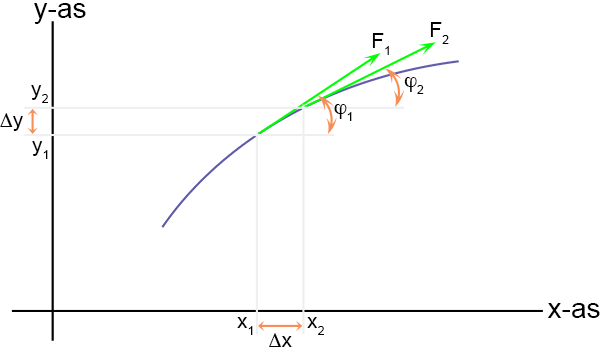
Ik zoom in op een heel klein stukje van het touw:
Voor de helling van het touw geldt:
De helling van het touw bij x
1 is:
En de helling van het touw bij x
2 is:
Het verschil tussen beide hellingen is:
Voor kleine verticale uitwijkingen geldt dat
tangens φ (nagenoeg) gelijk is aan
sinus φ (en mocht de verticale uitwijking
niet klein zijn, dan roteer ik simpelweg mijn assenstelsel zodanig dat de verticale uitwijking wel klein is):
En F
1 = F
2 = F, want het gaat in de noemers van vergelijking (5) puur om de grootte
van die krachten en niet om de richting (en ik verwaarloos de wrijving).
Vergelijking (5) wordt dan:
In het geval dat x
2 nadert naar x
1 gaat vergelijking (6) over in:
Hetgeen ik ook kan schrijven als:
Vervolgens ga ik Newton’s wet F = ma toepassen:
Ik introduceer ρ als massadichtheid van het touw:
Tenslotte
differentieer ik deze vergelijking naar de tijd:
Zoals gezegd verwaarloos ik de wrijving, dus F = constant, en ik ga er ook van uit dat het touw zijn vorm behoudt
en dat daarmee de massadichtheid ρ constant is.
Het quotiënt van beide is dan uiteraard ook constant en dat quotiënt noem ik K:
In vergelijking (12) is v
y de snelheid van het touw in de y-richting en deze grootheid ga ik
veralgemeniseren en vervolgens buiten haakjes brengen:
Die
tweede afgeleide naar x kan ik middels
de nabla-operator veralgemeniseren naar drie dimensies:
En met behulp van d'Alembertiaan kan ik dit nog compacter opschrijven als volgt:
Ziehier de algemene golfvergelijking:

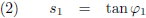
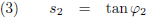
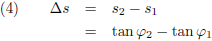
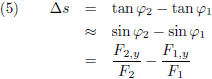
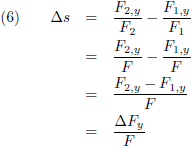
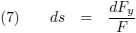
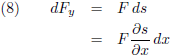
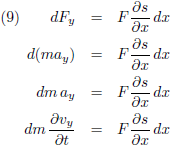
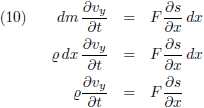
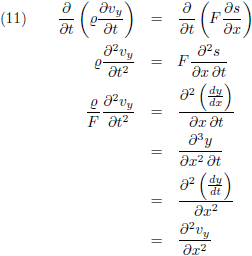
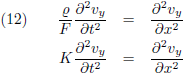
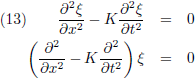
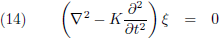
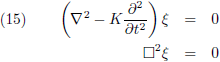

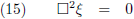


 Door naar het volgende vraagstuk: oplossing voor de algemene golfvergelijking
Door naar het volgende vraagstuk: oplossing voor de algemene golfvergelijking Terug naar het vorige vraagstuk: de Boltzmann-verdeling
Terug naar het vorige vraagstuk: de Boltzmann-verdeling Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Differentiëren
Differentiëren Goniometrie in het platte vlak
Goniometrie in het platte vlak De Euler-Maclaurin-formule
De Euler-Maclaurin-formule Bijzondere figuren
Bijzondere figuren Involuties
Involuties Oplossing voor de wet van Poisson
Oplossing voor de wet van Poisson Het Casimir-effect
Het Casimir-effect De illusie van pijn en lijden
De illusie van pijn en lijden De reis naar de werkelijkheid van Anita Moorjani
De reis naar de werkelijkheid van Anita Moorjani Dansen in de wolken
Dansen in de wolken Trefwoorden
Trefwoorden De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 16
Vectoren, vraagstuk 16 Vectoren, vraagstuk 54
Vectoren, vraagstuk 54 Vectoren, vraagstuk 92
Vectoren, vraagstuk 92 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen