Het Casimir-effect
Hoe bereken je het Casimir-effect?
Het Casimir-effect is vernoemd naar onze landgenoot Hendrik Casimir.
In 1948 publiceerde hij een artikel met daarin de afleiding voor dit effect.
- Geïnteresseerd in het oorspronkelijke artikel?
Stuur mij dan een email (karel@voorbijeinstein.nl)
met als onderwerp “PDF bestand 020301000001” en ik stuur je de file (gratis) toe.
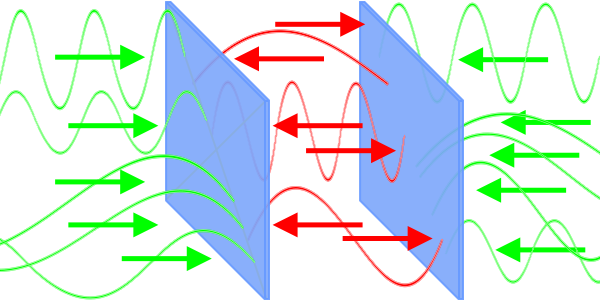
We volgen de afleiding zoals Casimir die in zijn artikel uiteen heeft gezet.
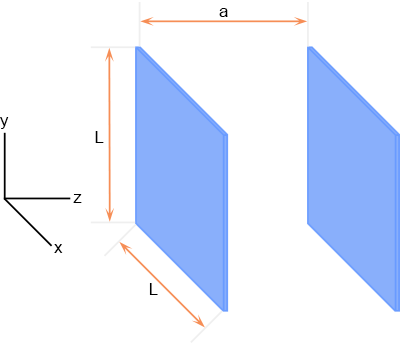
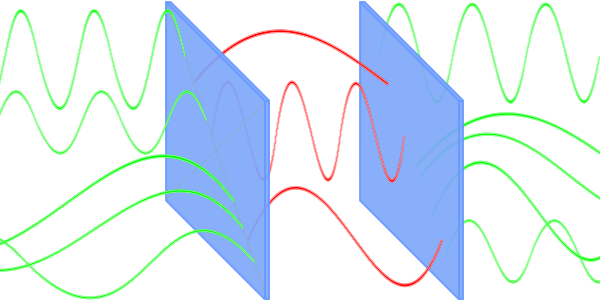
Hij gaat uit van een kubus (die ik niet getekend heb in het plaatje hiernaast) die gemaakt is van een perfect
geleidend materiaal, iedere ribbe van de kubus heeft de lengte L, en in de kubus bevindt zich een vierkante plaat
parallel aan het x-y-vlak (het x-y-vlak is een bepaalde zijde van de kubus).
Deze plaat is van hetzelfde perfecte geleidende materiaal gemaakt, kan bewegen in de z-richting, en de afstand
tot het x-y-vlak noemen we a.
We gaan ervan uit dat de lengte L zeer groot is ten opzichte van de golflengtes van de kwamtum-verschijnselen in de kubus.
Voor de ruimte R tussen de beweegbare plaat en het x-y-vlak geldt:
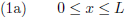
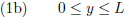
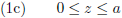 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
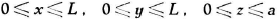
In lijn met het onzekerheidsprincipe van Heisenberg,
want dat principe eist dat de energie in een ruimte nooit exact nul kan worden omdat dat
zekerheid zou geven over de hoeveelheid energie in die ruimte, verschijnen er aan de lopende band energietjes (virtuele deeltjes).
Al deze energietjes, ieder met een willekeurige frequentie f, voldoen uiteraard aan de wet van Planck:
In de ruimte R kunnen alleen die energietjes bestaan/overleven waarvan een geheel aantal
halve golflengtes passen
tussen de wanden van de ruimte, want anders is er geen staande golf en dooft de golf uit.
De golflengte is λ en er geldt dus (waarbij n een positief geheel getal is):
Voor het
golfgetal k geldt:
Let op: het golfgetal komt in de literatuur en op internet ook voor als simpelweg de reciproke van de golflengte, dus zonder de factor 2π.
Casimir gebruikt hier wel de factor 2π en daarom doe ik het natuurlijk ook.
Hiermee worden de vergelijkingen (3):
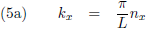
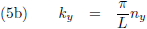
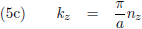 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
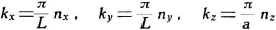
En tevens geldt:
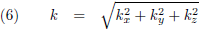 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
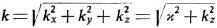
Ik stel:
Daarmee wordt vergelijking (6):
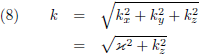 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
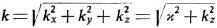
In de x-richting en in de y-richting kan iedere willekeurige frequentie/golflengte zich vormen, maar niet in de z-richting want daar vormen zich
alleen die golven waarvan een geheel aantal halve golflengtes tussen de platen past.
Indien ik alle energie tussen de platen (die gevormd wordt door de virtuele deeltjes) wil bepalen dan zal ik al die frequenties/golflengtes
moeten optellen (de factor half staat er bij in omdat het om veelvouden van
halve golflengtes gaat):
Dit zijn de frequenties tussen de platen.
Om hier energie van te maken moet ik vermenigvuldigen met de constante van Planck:
En dit is nog niet de hele waarheid, want de virtuele deeltjes hebben
twee vrijheidsgraden in hun polarisatie.
Daarom moet ik ook nog vermenigvuldigen met een factor twee:
In de x-richting en de y-richting kan n iedere waarde aannemen (niet noodzakelijkerwijs een geheel getal), en daarom verandert vergelijking (11) in:
Met behulp van de vergelijkingen (5) kan ik ook schrijven:
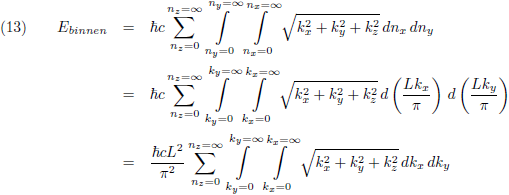 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
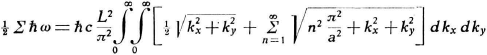
Voor n
z = 0 is er maar één polarisatiemogelijkheid (in plaats van twee).
Casimir sleept in zijn afleiding telkens een factor half mee voor n
z = 0 (zoals het eigenlijk hoort),
maar omdat dat uiteindelijk toch geen invloed heeft op het eindresultaat heb ik dat (voor de overzichtelijkheid) weggelaten.
Ik ga nu overstappen op poolcoördinaten.
Voor een infinitesimaal oppervlakje dA geldt in Cartesische coördinaten respectievelijk poolcoördinaten:
Dit vertaal ik als volgt naar het probleem dat we hier proberen op te lossen:
En dat ga ik toepassen in vergelijking (13):
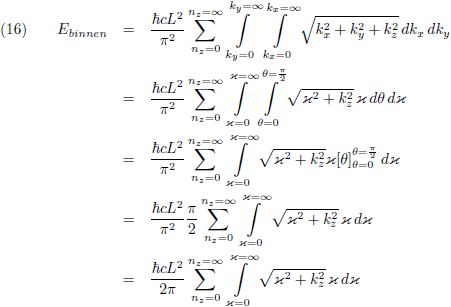 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
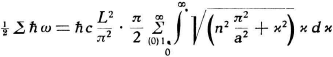
Voor de energie buiten de platen is het ook een kwestie van frequenties sommeren, maar daar kan ik ook in de z-richting
integreren omdat n
z
daar iedere waarde kan aannemen (niet noodzakelijkerwijs een geheel getal):
Het energieverschil tussen binnen-de-platen en buiten-de-platen is het verschil van de vergelijkingen (16) en (17):
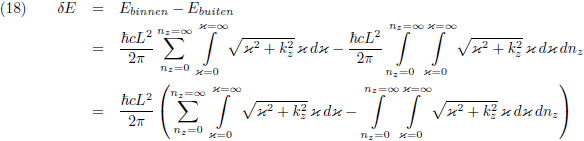 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
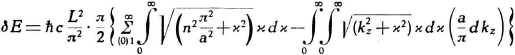
Ik introduceer een nieuwe variabele u:
Waaruit volgt:
Hiermee ga ik vergelijking (18) omschrijven:
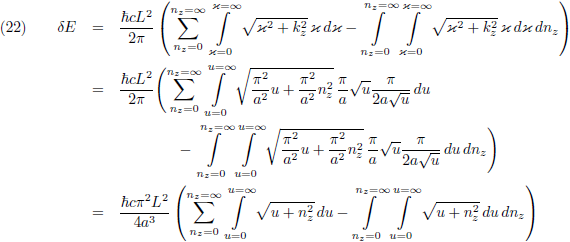 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
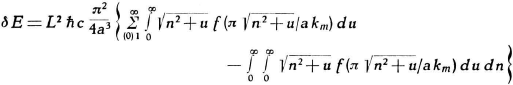
Ik introduceer nogmaals een nieuwe variabele, w:
Dit verandert vergelijking (22) in:
Er is niet zo heel veel fantasie voor nodig om in te zien dat bovenstaande
integralen het onbruikbare antwoord oneindig op gaan leveren.
Hoe nu verder?
Dit vraagt om een truc:
renormalisatie (het wegwerken van oneindigheden).
Ik stel:
Dan wordt (24):
Ik introduceer een functie g binnen de functie f:
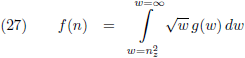 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
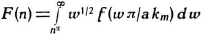
Voor deze functie g eis ik het volgende:
Ik kan de functie g bijvoorbeeld simpelweg een e-macht
meegeven die er voor zorgt dat voor lage waarden van w de functiewaarde één is, maar dat de
functiewaarde naar nul nadert voor hoge waarden van w.
De rechtvaardiging voor het invoegen van de functie g is:
- oneindig bestaat niet in de werkelijkheid maar alleen in onze wiskundige abstracties,
- voor hoge frequenties (Casimir noemt Röntgen-straling als voorbeeld) worden de platen transparant,
- zoals we de wereld nu zien gaan we ervan uit dat de Planck-eenheden grenzen zijn van de natuurkunde zoals
we die nu kennen, 1/Planck-tijd (bijvoorbeeld) zou dan logischerwijs een maximale frequentie zijn.
Kortom, er moet wel ergens een limiet zijn aan het aantal op te tellen frequenties en die brengen we er in middels de functie g.
Hierdoor kan ik de
integraal
van vergelijking (27) wél oplossen, want ik ga er nu van uit dat de
primitieve functie nul is voor w = ∞
(en dat is inderdaad lang niet altijd waar, bijvoorbeeld de functies f (x) = 0 en f (x) = 1/x zijn nul in oneindig maar de
primitieve functies
zijn daar zeker niet nul want in het eerste geval is F (x) = c en in het tweede geval is F (x) = ln x, kortom,
op het betoog van meneer Casimir is hier nog wel het een en ander op te merken (maar zijn eindresultaat klopt wel hoor)):
Dit resultaat vul ik in in (26):
Brengt dit een oplossing dichterbij?
Jawel!
We gaan gebruik maken van de Euler-Maclaurin-formule:
Hierin zijn de B’s de Bernoulli-getallen
(B1 = −1/2, B2 = 1/6,
B3 = 0, B4 = −1/30,
B5 = 0, B6 = 1/42, B7 = 0, B8 = −1/30,
B9 = 0, B10 = 5/66,
voor meer Bernoulli-getallen zie deze pagina).
Voor a en b vullen we nul respectievelijk oneindig in:
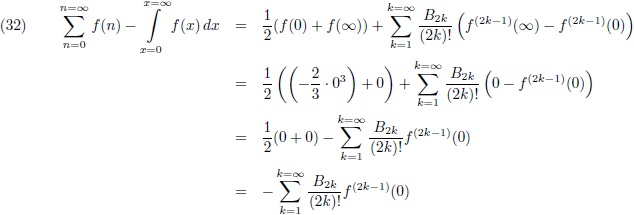 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
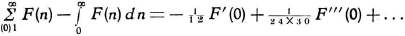
Ik ga eens even wat
afgeleiden bepalen:
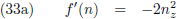
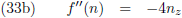
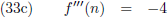
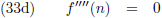 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
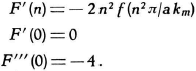
En alle hogere
afgeleiden zijn uiteraard ook nul.
Merk op dat indien ik hiervoor die vervelende oneindig er niet uit gewerkt had, dat die er dan nu wel uit gevallen zou zijn.
Oneindig is immers gewoon een getal (een heeeeeeeeeel groot getal weliswaar, maar desalniettemin een getal) en de
afgeleide van een getal, een constante, is nul.
Dit ga ik gebruiken in vergelijking (32) en ik vul ook de Bernoulli-getallen in:
Hiermee wordt de oplossing van (30):
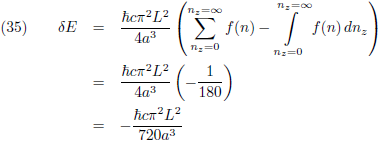 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
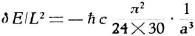
Door deze (verschil)energie te
differentiëren
naar de afstand a krijg ik de kracht (het verschil tussen de rode en groene pijlen, die niet op schaal
getekend zijn, in het plaatje hierboven):
Per vierkante meter plaat wordt dit:
Alle constanten zoek ik op in de
tabel met fysische gegevens
waarna een rekenmachine mij vertelt:
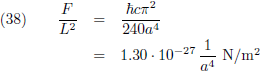 Oorspronkelijke vergelijking uit het artikel van Casimir:
Oorspronkelijke vergelijking uit het artikel van Casimir:
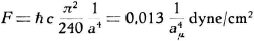
Twee opmerkingen tot slot:
- het moge duidelijk zijn dat we het hier hebben over een minimaal krachtje die ook nog eens afneemt met de vierde
macht van de afstand,
- als je meer wilt weten over het onzekerheidsprincipe van Heisenberg ga dan door naar het
volgende vraagstuk.

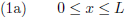
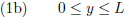
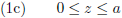
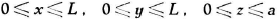
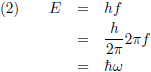
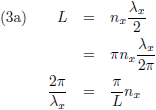
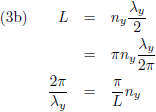
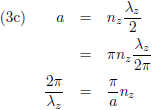
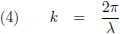
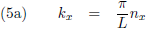
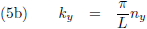
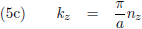
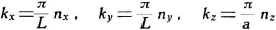
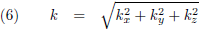
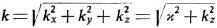
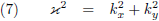
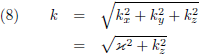
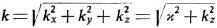
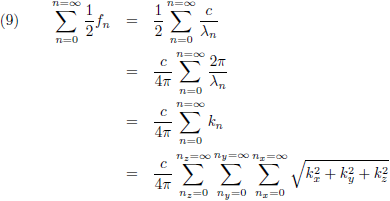
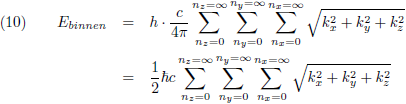
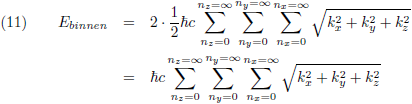
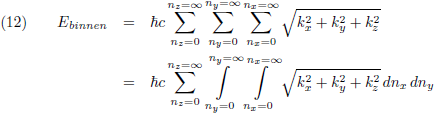
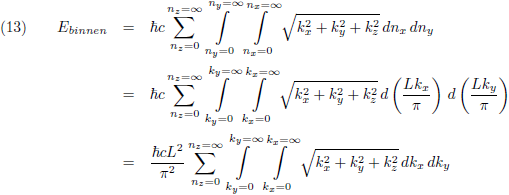
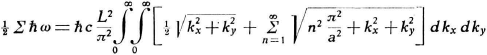
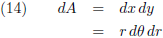
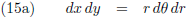
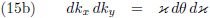
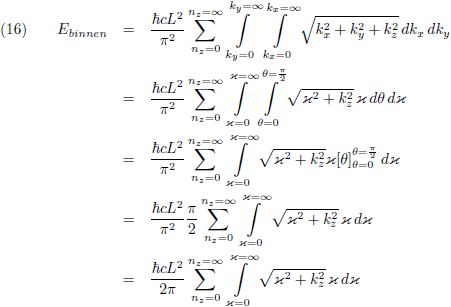
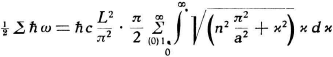
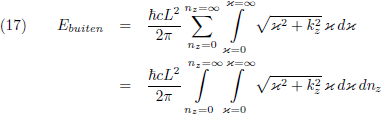
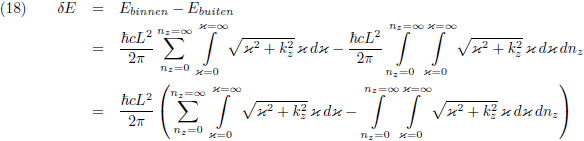
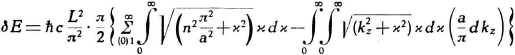
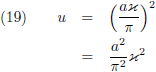
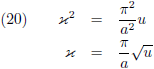
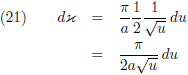
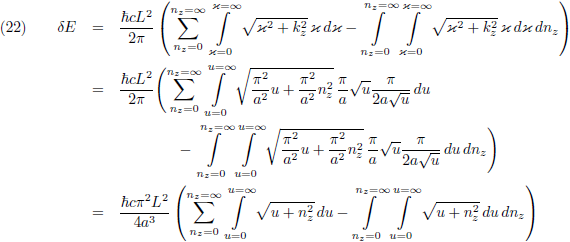
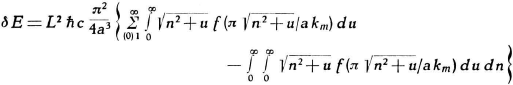
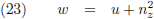
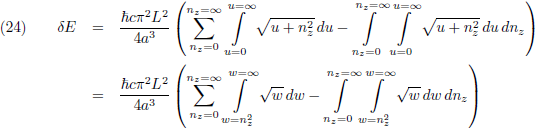
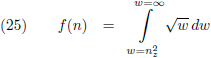
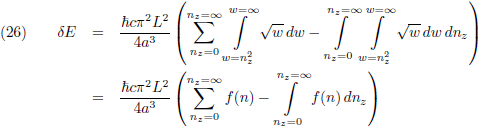
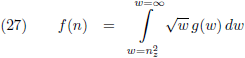
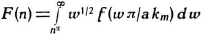
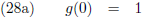
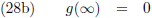
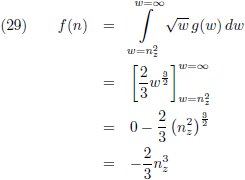
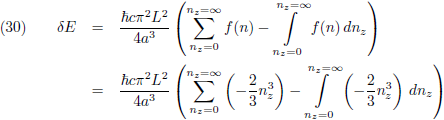
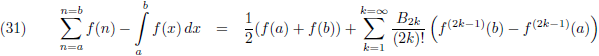
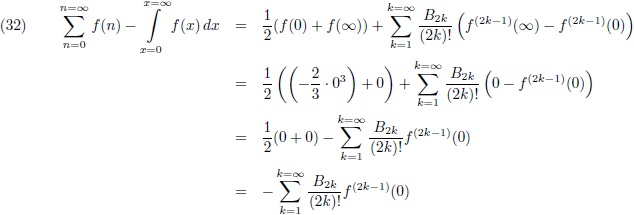
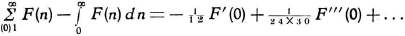
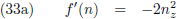
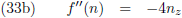
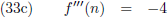
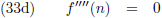
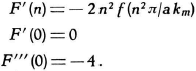
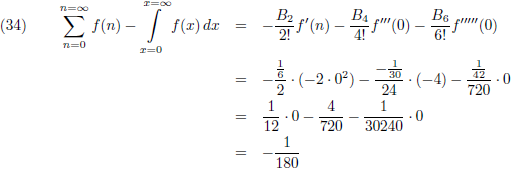
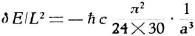
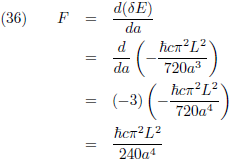
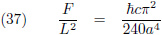
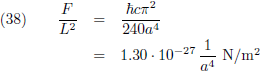
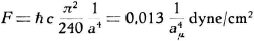







 Door naar het volgende vraagstuk: een analogie van het onzekerheidsprincipe van Heisenberg
Door naar het volgende vraagstuk: een analogie van het onzekerheidsprincipe van Heisenberg Terug naar het vorige vraagstuk: de energie die een zwart voorwerp uitstraalt
Terug naar het vorige vraagstuk: de energie die een zwart voorwerp uitstraalt Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina kwantummechanica
Naar de overzichtspagina kwantummechanica Fourier-analyse van het onzekerheidsprincipe van Heisenberg (II)
Fourier-analyse van het onzekerheidsprincipe van Heisenberg (II)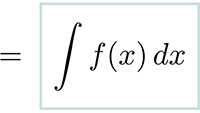 Integreren
Integreren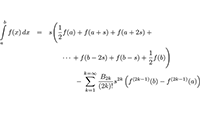 De Euler-Maclaurin-formule
De Euler-Maclaurin-formule Differentiëren
Differentiëren Machtsverheffen, worteltrekken, logaritme nemen
Machtsverheffen, worteltrekken, logaritme nemen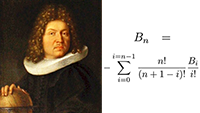 Bernoulli-getallen
Bernoulli-getallen Fysische gegevens
Fysische gegevens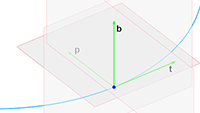 Differentiaal geometrie
Differentiaal geometrie Herkomst van de Odyssee
Herkomst van de Odyssee De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 35
Vectoren, vraagstuk 35 Vectoren, vraagstuk 73
Vectoren, vraagstuk 73 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van Het touw om de Maan
Het touw om de Maan Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen