De integraal van
f (x) = sin x/(1 − a2 sin2 x)1/2
Trefwoorden/keywords: integraal/integral, integreren/integrate, f (x) = sin x/(1 − a2 sin2 x)1/2
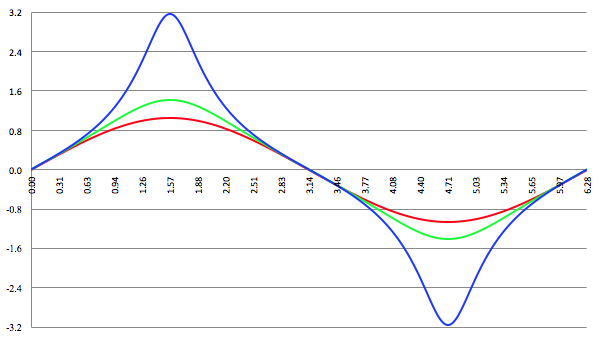
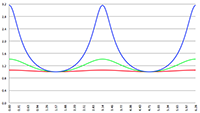
De grafiek van f (x) = sin x/(1 − a
2 sin
2 x)
1/2 voor a
2 = 0.1 (de rode lijn),
a
2 = 0.5 (de groene lijn) en a
2 = 0.9 (de blauwe lijn)
Deze
integraal vereist een paar trucs.
Om te beginnen ga ik die
sinus
in de noemer omzetten naar een
cosinus:
Ik stel:
Zodat de
integraal deze vorm krijgt:
Ik stel:
Zodat ik de
integraal in deze vorm kan schrijven:
De oplossing van de
integraal
van 1/(a
2 + x
2)
1/2 kun je elders vinden in de
tabel met integralen.
Dat brengt ons bij dit tussenresultaat:
Nu moet t uiteraard weer vervangen worden door x:
En b moet uiteraard weer vervangen worden door a:
Tot slot wil ik nog opmerken dat je de
area sinus hyperbolicus
kunt
omschrijven naar een
natuurlijke logaritme,
en vice versa, als volgt:
De oplossing van deze
integraal
kan ik daarom ook als volgt opschrijven:
En dit kan ik ook opschrijven als volgt:
Ter controle ga ik het resultaat
differentiëren:
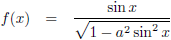

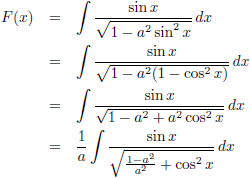
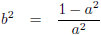
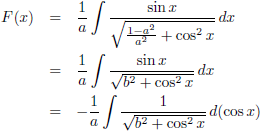

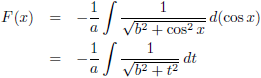
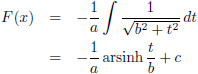
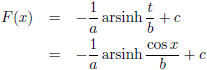
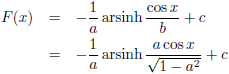
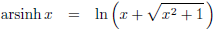
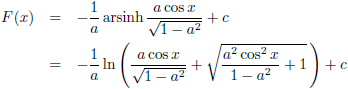
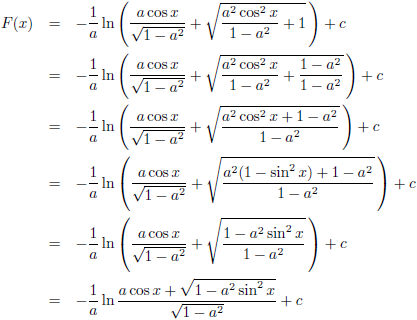

 Door naar de volgende integraal: de integraal van
Door naar de volgende integraal: de integraal van Terug naar de vorige integraal: de integraal van
Terug naar de vorige integraal: de integraal van Tabel met integralen
Tabel met integralen Tabel met afgeleiden
Tabel met afgeleiden Tabel met Taylor-reeksen
Tabel met Taylor-reeksen Integreren
Integreren Differentiëren
Differentiëren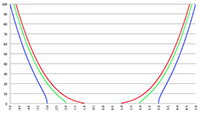 De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van Inwendig product, uitwendig product en dyadisch product
Inwendig product, uitwendig product en dyadisch product Vectoren, vraagstuk 35
Vectoren, vraagstuk 35 Vectoren, vraagstuk 73
Vectoren, vraagstuk 73 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT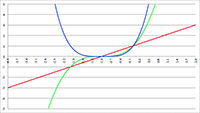 De Taylor-reeks van
De Taylor-reeks van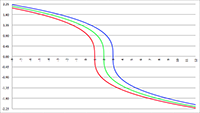 De Taylor-reeks van
De Taylor-reeks van Het touw om de Maan
Het touw om de Maan Relativiteitstheorie rekenkundig, hoofdstuk 9: nabeschouwingen
Relativiteitstheorie rekenkundig, hoofdstuk 9: nabeschouwingen De snelheid van een meertrapsraket
De snelheid van een meertrapsraket Het relativistische impulsmoment van een massieve bol
Het relativistische impulsmoment van een massieve bol Astronomie
Astronomie Elektriciteit en magnetisme
Elektriciteit en magnetisme Hoe ziet de wereld er morgen uit?
Hoe ziet de wereld er morgen uit? Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen