De afgeleide van
f (x) = ϑ (a)
Trefwoorden/keywords: afgeleide/derivative, differentiëren/differentiation, f (x) = ϑ (a)
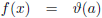
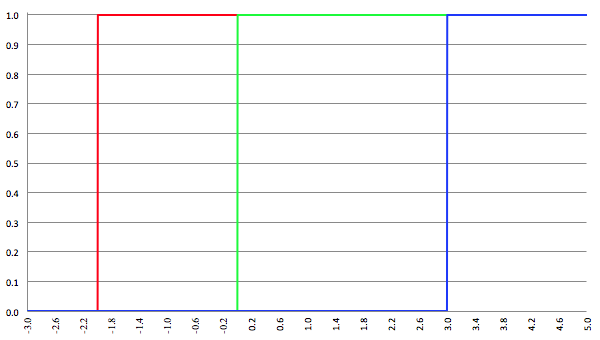
De grafiek van f (x) = ϑ (a) voor a = −2 (de rode lijn),
a = 0 (de groene lijn) en a = 3 (de blauwe lijn)
Deze functie heet de Heaviside-stapfunctie. Voor x < a is de functiewaarde gelijk aan nul en voor x > a is de functiewaarde gelijk aan één. In dat ene punt waar x = a springt de functiewaarde instantaan van nul naar één en daar is de functie dan ook niet gedefinieerd.
De afgeleide van deze functie is overal nul waar de functie horizontaal loopt, dus waar x ongelijk aan a is. In het punt x = a springt de functiewaarde instantaan van nul naar één en is het hellingsgetal van de functie gedurende een infinitesimaal moment oneindig. De functie die daardoor ontstaat heet de Dirac-deltafunctie. De afgeleide wordt dan:
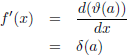
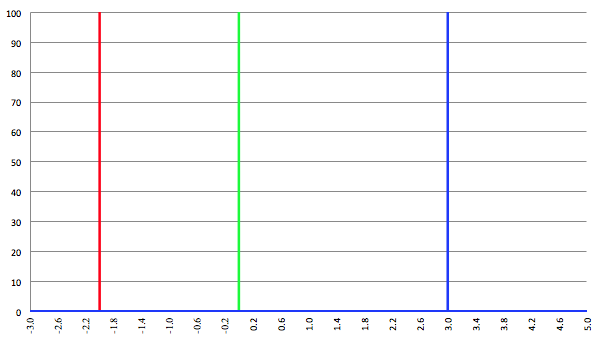
De grafiek van f' (x) voor a = −2 (de rode lijn),
a = 0 (de groene lijn) en a = 3 (de blauwe lijn)
Door naar de volgende afgeleide: de afgeleide van
Terug naar de vorige afgeleide: de afgeleide van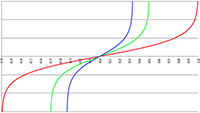
Tabel met afgeleiden
Tabel met integralen
Tabel met Taylor-reeksen
De integraal van
De integraal van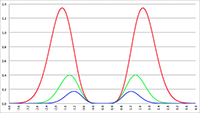
De integraal van
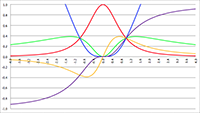De integralen van
Vectoren, vraagstuk 14
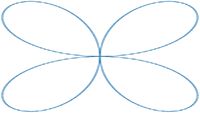Vectoren, vraagstuk 52
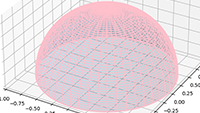Vectoren, vraagstuk 90
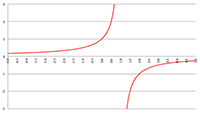De Taylor-reeks van
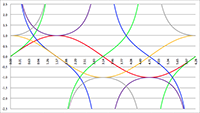De Taylor-reeksen van
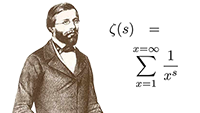De Riemann-zeta-functie
Uitleg artikel algemene relativiteitstheorie: paragraaf 12
De lengtecontractie van een trein
De Ricci-tensor van de Schwarzschild-metriek
Periheliumprecessie als gevolg van een oblate ster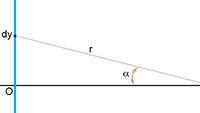
Het elektrische veld van een lange geladen geleider
De illusies die wij leven
De illusie van brieven uit de toekomst
Programmering en werkelijkheid
Voorbeelden van E = mc2
De pijn die je voelt wanneer je in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt
De Euler-Lagrange-vergelijking
De baan van een baksteen bij een zwart gat
De Taylor-reeks van f (x) = tan (ax)
De integralen van f (x) = sin2 x/(1 + a cos x)2
De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De invaltijd van een baksteen die in een zwart gat valt
Naar de overzichtspagina wiskunde
Naar de overzichtspagina natuurkunde
Naar de overzichtspagina filosofie
Doneer enkele euro’s
Wetenschappelijke boeken te koop
Lezingen