De lengtecontractie van een trein
Hoe zou je de lengtecontractie van een rijdende trein kunnen bepalen?
Je staat op een perron, er dendert een trein voorbij, en de relativiteitstheorie leert ons dat die trein
een lengtecontractie ondergaat als gevolg van de snelheid die die trein heeft ten opzichte van jou, de
waarnemer op het perron.
Hoe zou je die lengtecontractie kunnen bepalen?
Er is een hele simpele methode die altijd werkt.
Wanneer de trein (nog) stil staat meet je op je gemak met een (hele nauwkeurige) liniaal of rolmaat of duimstok
de lengte van de trein op, deze lengte noemen we L
1.
Vervolgens verlaat je de trein en de trein vertrekt.
Dit klusje had je natuurlijk ook kunnen laten doen door iemand in de trein terwijl de trein reed, en die persoon
belt of appt je vervolgens het resultaat door.
Op het perron zet je twee streepjes waarvan je heel nauwkeurig de tussenliggende afstand meet.
Jij gaat bij het ene streepje staan en een assistent gaat bij het andere streepje staan.
Je hebt beide een nauwkeurig uurwerk paraat en jullie zorgen dat die precies gelijk lopen.
Dit kun je allemaal op je gemak uitvoeren, je hebt alle tijd van de wereld.
Dan komt het moment suprème, de trein dendert voorbij en jullie lezen allebei het tijdstip af dat de voorkant van
de trein het streepje passeert.
Tenslotte leest een van jullie ook nog het tijdstip af dat de achterkant van de trein het streepje passeert.
De trein is gepasseerd en jij en de assistent lopen naar elkaar toe.
Uit de tijden die jullie geklokt hebben bij het passeren van de voorkant van de trein is de snelheid van de
trein te berekenen:
En degene die ook nog geklokt heeft wanneer de achterkant voorbij kwam kan daarmee de lengte van de trein
uitrekenen:
De lengtecontractie van de trein is aldus:
Op zich is er helemaal niets mis met deze methode afgezien van de praktische uitvoerbaarheid.
De lengtecontractie van een hogesnelheidstrein op topsnelheid is nog altijd veel minder dan de diameter van
één enkel atoom en om dat via bovenstaande methode te gaan meten is een heilloze onderneming.
Tijd kunnen we heel nauwkeurig meten, dus een methode waarbij we geen gebruik hoeven te maken van linialen
en dat soort afstandsmeters, en alleen maar tijdsintervallen meten, zou al een enorme stap vooruit zijn.
Kijk eens naar de volgende meetopstelling.
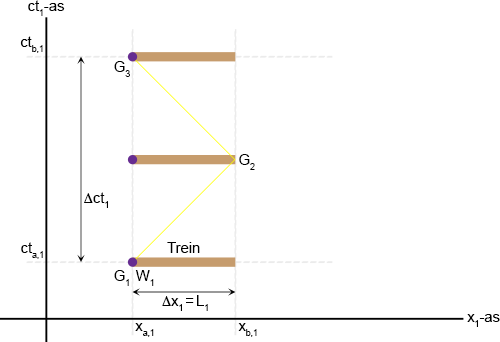
Er is een waarnemer, W
1, achterin de trein en die laat een lampje flitsen dat helemaal aan de
achterkant van de trein op positie x
a,1 is gemonteerd.
Deze lichtflits, op tijdstip ct
a,1, is gebeurtenis G
1.
Helemaal aan de voorkant van de trein bevindt zich een spiegeltje en gebeurtenis 2, G
2, is het
weerkaatsen van de lichtflits tegen dit spiegeltje.
Gebeurtenis 3, G
3 op tijdstip ct
b,1, is de terugkeer van dit licht bij W
1 en
hij/zij heeft geklokt hoelang het licht er over heeft gedaan om naar de voorkant van de trein te reizen en weer terug.
Gedurende het tijdsinterval ∆ct
1 = ct
b,1 − ct
a,1 was de lichtstraal
onderweg en heeft daarbij tweemaal de afstand ∆x afgelegd zijnde lengte L
1 van de trein.
W
1 kan uit de beide tijdstippen die hij geklokt heeft, vertrek lichtstraal en terugkeer lichtstraal, de
lengte van de trein berekenen:
Of de trein rijdt of stilstaat maakt allemaal niet uit voor W
1, onder alle omstandigheden (tenzij de trein
versnelt of afremt) zal hij tot dezelfde treinlengte komen.
Omdat W
1 in zijn stelsel niet beweegt kiest hij als x-coördinaat voor zijn positie
x
1 = x
a,1 = 0.
En om alles nog simpeler te maken kiest hij voor het moment dat de lamp flitst ct
1 = ct
a,1 = 0.
Daarmee wordt de vergelijking voor de lengte van de trein:
Een tweede waarnemer W
2 rijdt met W
1 mee en is getuige van de metingen die W
1 uitvoert.
Hij weet nu wat de uitkomst is van de metingen van W
1 en hij ziet ook dat de snelheid van de trein niet van
invloed is op het resultaat, zolang die snelheid maar constant is.
Vervolgens stapt W
2 uit de trein en gaat proberen buiten de trein de lengtemeting te reproduceren.
Hij maakt eveneens gebruik van de lichtflits die door W
1 geïnitieerd wordt en van de door de spiegel
teruggekaatste lichtflits.
Wanneer de trein passeert meet W
2 met behulp van twee sensoren, die op een voor hem bekende afstand staan,
de snelheid van de trein.
Daarna stapt hij op de rails zodat vanaf dat moment alles een eendimensionaal probleem wordt en kan W
1
beginnen met de lengtemeting van de trein.
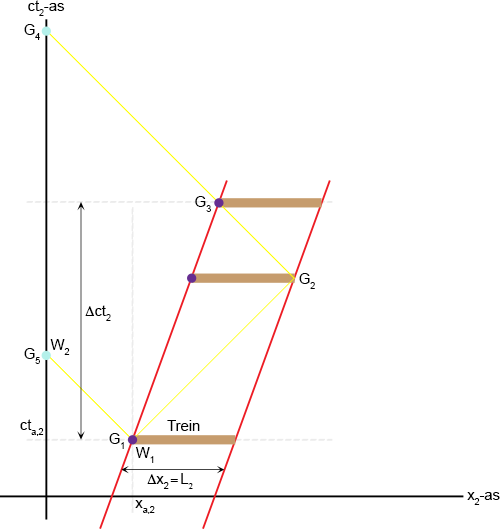
W
2 weet uiteraard niet wanneer W
1 de lamp laat flitsen en benoemt daarom deze gebeurtenis
G
1 met voor hem onbekende ruimtetijdcoördinaten (x
a,2, ct
a,2).
De flitsende lamp stuurt een lichtstraal naar de voorkant van de trein, de vergelijking hiervan is:
Met b een onbekende constante, maar die kunnen we te weten komen door de coördinaten van G
1 in te vullen:
Zodat de vergelijking van de lichtstraal wordt:
We kunnen ook de vergelijking opstellen van de achterkant van de trein:
Met b een onbekende constante, maar die kunnen we wederom te weten komen door de coördinaten van G
1 in te vullen:
Zodat de vergelijking van de achterkant van de trein wordt:
De vergelijking van de voorkant van de trein is nagenoeg identiek hieraan, maar dan een treinlengte L
2 ‘verderop’:
Er gaat ook een lichtstraal van de achterkant van de trein naar W
2 (aankomst bij W
2 is G
5).
De vergelijking hiervan is:
Met b een onbekende constante, maar ook die kunnen we te weten komen door de coördinaten van G
1 in te vullen:
Zodat de vergelijking van de lichtstraal wordt:
Omdat W
2 in zijn stelsel niet beweegt kiest hij, net als W
1 als x-coördinaat voor zijn positie
x
2 = x
a,2 = 0.
Door dit in te vullen in de laatste vergelijking vinden we de tijdcoördinaat van G
5:
De coördinaten van G
2 vinden we door het snijpunt uit te rekenen van de voorkant van de trein en de lichtstraal
die daar naar toe op weg is:
De tijdcoördinaat die hierbij hoort is:
Vanaf de spiegel weerkaatst de lichtstraal terug richting de achterkant van de trein, de vergelijking hiervan is:
Met b een onbekende constante, maar die kunnen we te weten komen door de coördinaten van G
2 in te vullen:
Zodat de vergelijking van de lichtstraal wordt:
De coördinaten van G
3 vinden we door het snijpunt uit te rekenen van de achterkant van de trein en de lichtstraal
die daar naar toe op weg is:
De tijdcoördinaat die hierbij hoort is:
De lichtstraal die vanaf de voorkant op weg is naar W
1 is ook op weg naar W
2.
De aankomst bij W
2 is G
4 en daar is x
2 = 0:
Laat ik even alles op een rijtje zetten:
Het tijdsverschil tussen G
5 en G
4 is voor W
2:
Uit dit tijdsinterval, dat W
2 geklokt heeft, kan hij de treinlengte L
2 berekenen.
Het tijdsverschil tussen G
1 en G
3 is voor W
1:
En het tijdsverschil tussen G
1 en G
3 is voor W
2:
De verhouding van beide is:
Deze afleiding kan zowel door W
1 als door W
2 gedaan worden.
Hoe moeten we dit resultaat duiden?
W
1 en W
2 weten dat hun wederzijdse tijden dilateren met een factor γ.
Kritische noot: weten ze dat?
Ik zeg “ja”, want tijddilatatie is een experimenteel bewezen/gemeten feit.
Wanneer we dit verwerken in de tijdsintervallen ∆ct
G1 → G3
in bovenstaande vergelijking dan houden we over:
Met andere woorden, W
2 meet een treinlengte L
2 die een factor γ korter is dan
de treinlengte L
1 zoals gemeten door W
1: lengtecontractie.
Echter, nog steeds blijft al het voorafgaande gereken aan de lengte van een rijdende trein puur een
mathematische excursie.
Zoals gezegd is de lengtecontractie van een trein veel minder dan de diameter van een atoom en een
dergelijke nauwkeurigheid is in de verste verte niet haalbaar.
Een trein dendert en trilt, ‘veegt’ allerlei troep op onderweg, rekt uit en krimpt weer in onder invloed
van de krachten die in de trein werkzaam zijn, er zijn temperatuursinvloeden, enzovoort.
De lijst is heel lang en dat overschaduwt de praktische uitvoerbaarheid volledig.


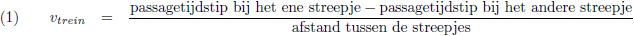
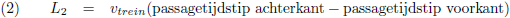
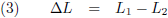
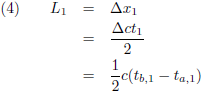
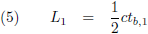
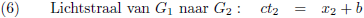
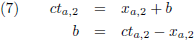
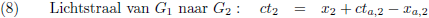

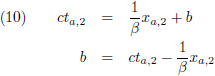
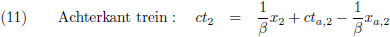
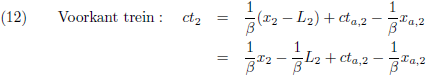
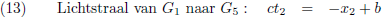
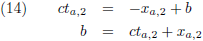
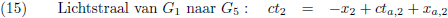
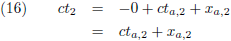
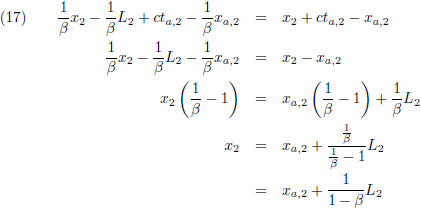
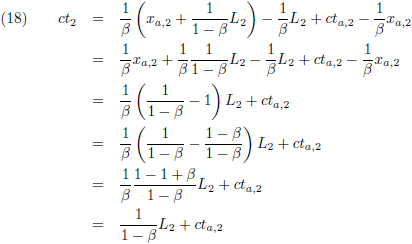
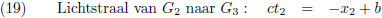
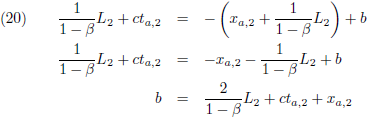
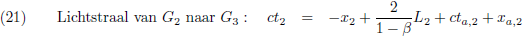
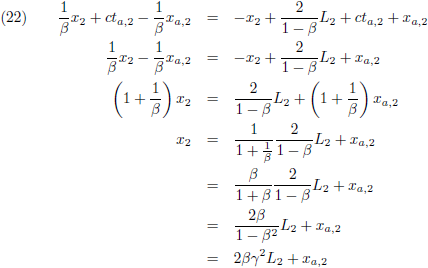
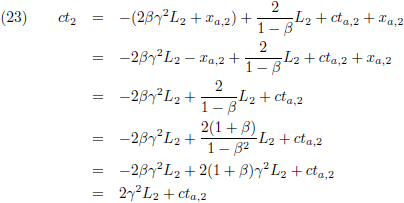
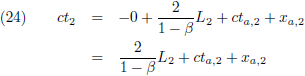
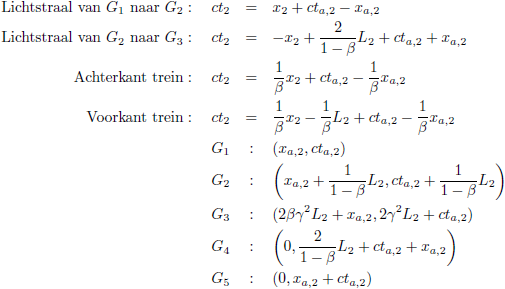
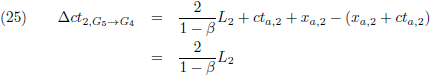
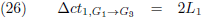
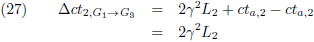
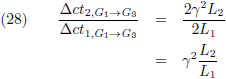
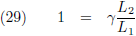
 Door naar het volgende vraagstuk: de automobilist die door rood reed
Door naar het volgende vraagstuk: de automobilist die door rood reed Terug naar het vorige vraagstuk: de Lorentz-factor
Terug naar het vorige vraagstuk: de Lorentz-factor Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 38
Vectoren, vraagstuk 38 Vectoren, vraagstuk 76
Vectoren, vraagstuk 76 Uitschrijven van de sommatieconventie
Uitschrijven van de sommatieconventie De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van De stelling van Green
De stelling van Green Uitleg artikel algemene relativiteitstheorie: voorpagina
Uitleg artikel algemene relativiteitstheorie: voorpagina Lijnen trekken door negen punten
Lijnen trekken door negen punten De transformatievergelijking voor versnelling
De transformatievergelijking voor versnelling Hemelmechanica
Hemelmechanica Het elektrische veld in een kooi van Faraday
Het elektrische veld in een kooi van Faraday Wanneer heb je voor het laatst iets nieuws gedaan?
Wanneer heb je voor het laatst iets nieuws gedaan? De illusie dat het goed gaat met mij
De illusie dat het goed gaat met mij Vertellingen
Vertellingen Reisverslag Georgië
Reisverslag Georgië Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen