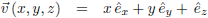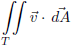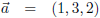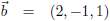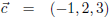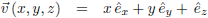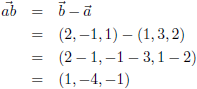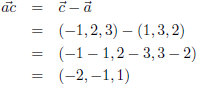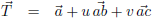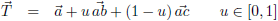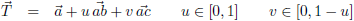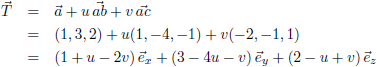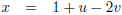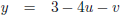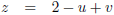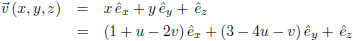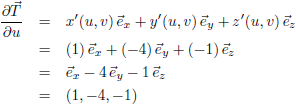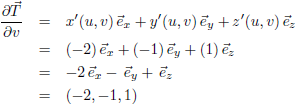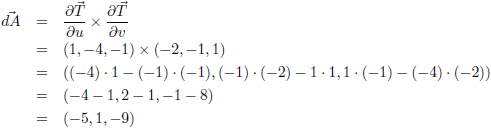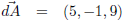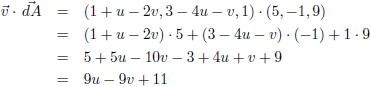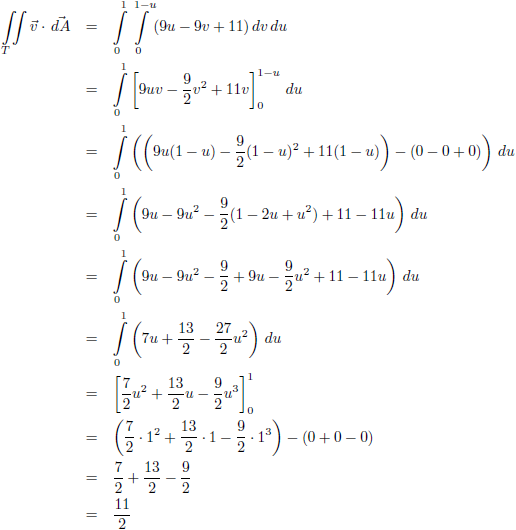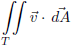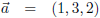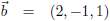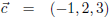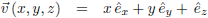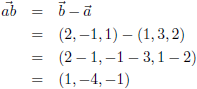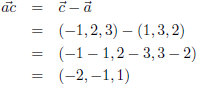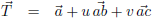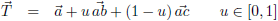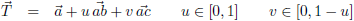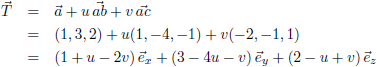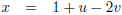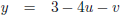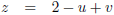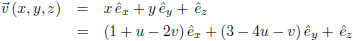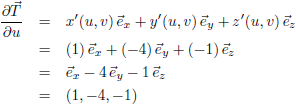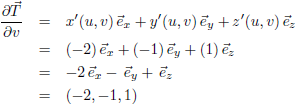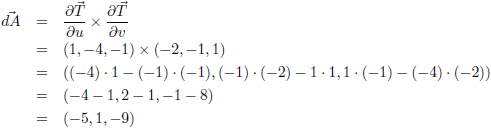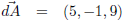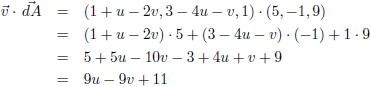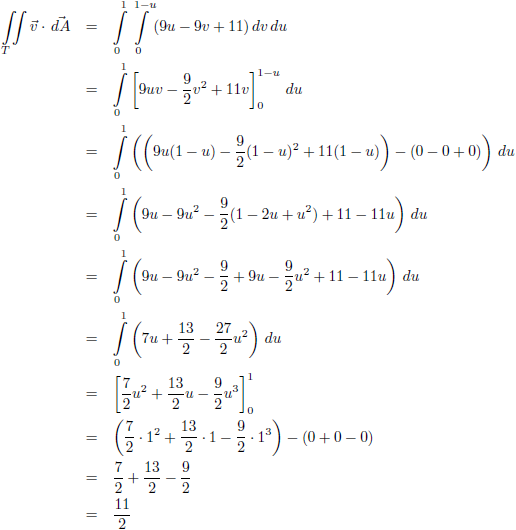Vectoren, vraagstuk 79
Bereken de volgende
integraal:
Waarbij T de driehoek is met hoekpunten:
Deze driehoek heeft een naar boven gerichte eenheidsnormaal en het vectorveld
v is:
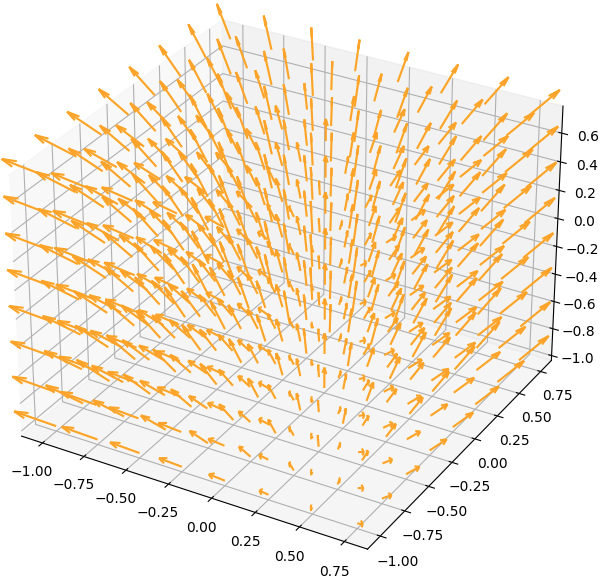
Het vectorveld
v
Ik ga eerst twee richtingsvectoren berekenen voor het vlak T:
Dan kan ik T beschrijven als volgt:
Echter, op deze manier beschrijf ik de totale tweedimensionale ruimte waar de punten
a,
b en
c zich in bevinden.
Ik zal wat beperking aan moeten brengen:
Dit is beter, maar nu beschrijf ik een parallellogram in plaats van een driehoek.
Er moet een afhankelijkheid tussen u en v ingebracht worden:
Dit is het ook niet want nu heb ik de beschrijving van een lijn.
De afhankelijkheid tussen u en v moet ik ergens anders zoeken:
Dit is de juiste beschrijving van de driehoek T.
Ik schrijf T even iets anders op:
Hieruit kan ik aflezen dat:
Daarmee kan ik het vectorveld ook schrijven als:
Vervolgens bepaal ik de
partiële afgeleiden van T:
Het is niet verrassend dat dit uiteraard weer de beide richtingsvectoren oplevert.
Het
uitwendig product
hiervan is
dA en dit is tevens de normaalvector:
Omdat de normaalvector naar boven gericht moet zijn (z-component > 0) dien ik
dA met −1 te vermenigvuldigen:
Het
inwendig product
v ∙
dA wordt dan:
Daarmee wordt de
integraal:
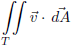 Waarbij T de driehoek is met hoekpunten:
Waarbij T de driehoek is met hoekpunten:
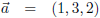
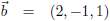
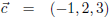 Deze driehoek heeft een naar boven gerichte eenheidsnormaal en het vectorveld v is:
Deze driehoek heeft een naar boven gerichte eenheidsnormaal en het vectorveld v is: