Het elektrische veld op de as van een geladen ring
Bereken het elektrische veld op de as van een geladen ring.
Ga uit van een vacuüm omgeving.
Ik heb een ring waar een elektrische lading Q op zit.
Mijn x-as kies ik zo dat die precies door het midden van de ring gaat en de oorsprong leg ik in
het midden van de ring.
Vervolgens ga ik bepalen wat het elektrische veld is in een punt P ergens op die x-as.
Daarvoor beschouw ik eerst een infinitesimaal stukje dl van de ring.
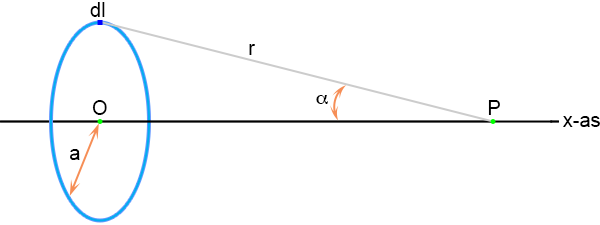
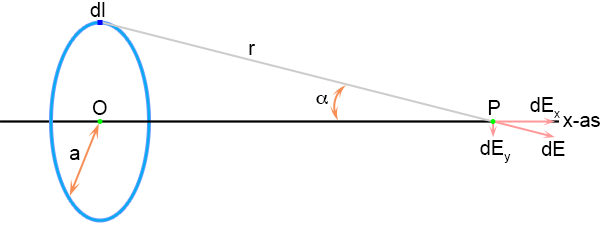
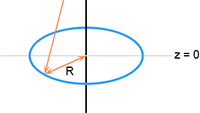
Ik heb een plaatje gemaakt van de situatie:
Voor de ladingsdichtheid van de ring geldt:
Het infinitesimale beetje lading op het stukje dl is dan:
Dit beetje lading veroorzaakt een elektrisch veld in het punt P volgens de wet van De Coulomb:
Dit veld is gericht langs r en kent een x-component en een y-component, zie het plaatje hieronder:
De y-component daar ben ik niet in geïnteresseerd, want om symmetrieredenen is nu al wel in te zien
dat de y-component van het veld in het punt P uiteindelijk als gevolg van de gehele ring nul zal zijn.
Daarom richt ik mij alleen op de x-component en komt er bij vergelijking (3) de
cosinus van α bij in:
En die
cosinus van α ga ik schrijven
als een functie van r en x:
En omdat voor r geldt:
Hiermee wordt vergelijking (5):
En de laatste stap is om dit te
integreren
over de totale omtrek van de ring:
Tenslotte wil ik die λ er weer uitwerken:
Merk op dat indien het punt P zich ‘heel ver weg’ bevindt dat vergelijking (9) dan overgaat in de
wet van De Coulomb, omdat van veraf de ring eruit ziet als een puntlading:
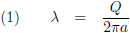
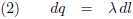
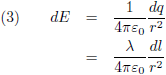
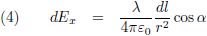
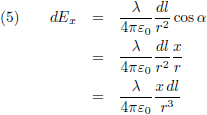
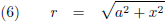
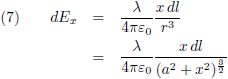
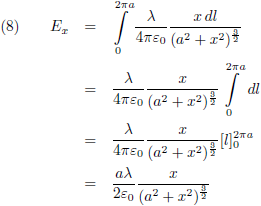
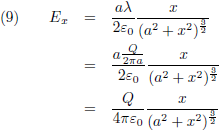
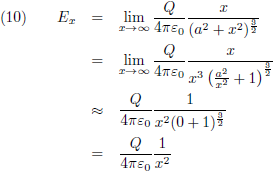

 Door naar het volgende vraagstuk: een elektron op de as van een geladen ring
Door naar het volgende vraagstuk: een elektron op de as van een geladen ring Terug naar het vorige vraagstuk: 1 gram elektronen in een kistje
Terug naar het vorige vraagstuk: 1 gram elektronen in een kistje Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina elektriciteit en magnetisme
Naar de overzichtspagina elektriciteit en magnetisme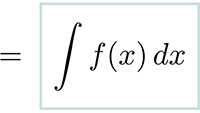 Integreren
Integreren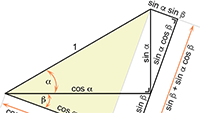 Goniometrie in het platte vlak
Goniometrie in het platte vlak De Taylor-reeksen van
De Taylor-reeksen van Een analogie van het onzekerheidsprincipe van Heisenberg
Een analogie van het onzekerheidsprincipe van Heisenberg Relativistische periheliumprecessie, 1e orde benadering
Relativistische periheliumprecessie, 1e orde benadering De illusie dat ik beter ben dan anderen
De illusie dat ik beter ben dan anderen Trump en de schoonheid van de werkelijkheid
Trump en de schoonheid van de werkelijkheid De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van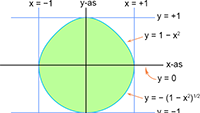 Vectoren, vraagstuk 29
Vectoren, vraagstuk 29 Vectoren, vraagstuk 67
Vectoren, vraagstuk 67 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van Boekhouden
Boekhouden Relativiteitstheorie rekenkundig, hoofdstuk 3: het balletje
Relativiteitstheorie rekenkundig, hoofdstuk 3: het balletje Uitleg artikel precessie van Mercurius: paragraaf 1
Uitleg artikel precessie van Mercurius: paragraaf 1 Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen