Lineariteit van de Lorentz-transformaties
Hoe weet je nou dat de Lorentz-transformaties lineair moeten zijn?
Dat de Lorentz-transformaties lineair zijn volgt uit de aanname
dat de ruimtetijd homogeen is.
Het bovenstaande plaatje laat (een deel van) de sterrenhemel zien waarbij gebruik gemaakt is van een lange sluitertijd.
Dus zowel ruimte als tijd zijn als het ware ‘gevangen’ in dit plaatje.
Het onzichtbare abstracte goedje dat je overhoudt wanneer je al die sterren (en planeten en nevels en
zwarte gaten en de
rest) wegdenkt noemen we ruimtetijd en we nemen aan dat dat homogeen is (overal dezelfde eigenschappen heeft).
Dat ziet er dan uit zoals op het plaatje hieronder.

Homogene ruimtetijd
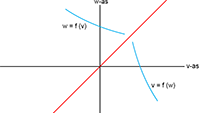
Stel ik ken aan een of andere gebeurtenis ergens in de ruimtetijd een viervector u toe:
Voor een passerende waarnemer W’, met een constante snelheid v, is die viervector:
Ik heb geen idee wat het verband is tussen de grootheden met en zonder accent, maar er zal een of andere transformatiefunctie
moeten bestaan (indien er geen transformatiefunctie bestaat dan is er sprake van willekeur en ligt het relativiteitsprincipe
in duigen):
Homogeniteit van de ruimtetijd impliceert dat de ruimte ‘hier’ niet anders is dan de ruimte ‘daar’ en dat de tijd ‘nu’ niet
anders is dan de tijd ‘straks’, of anders gezegd: de ruimtetijd heeft overal en altijd dezelfde eigenschappen.
Oftewel, wanneer ik een translatie uitvoer op de vector u dan is dat voor W’ ook een translatie:
Door vergelijking (3) te substitueren in (4) krijg ik:
Dit moet uiteraard ook gelden indien u een nulvector is:
Dit resultaat stop ik in de vorige vergelijking:
Dit ga ik nog iets anders opschrijven:
Ik stel:
Hiermee wordt vergelijking (8):
Stel dat
T =
u, dan volgt uit (10):
Stel dat
T = 2
u, dan volgt uit (10) en (11):
En stel dat
T = 3
u, dan volgt uit (10) en (12):
Zo kan ik natuurlijk eindeloos doorgaan, het moge duidelijk zijn dat voor ieder geheel getal n ik uitkom op:
Dit moet uiteraard ook gelden voor het product van twee gehele getallen n en m, want het product van twee gehele getallen
is ook een geheel getal:
En het gehele getal m kan ik altijd schrijven als het product van een reëel getal k maal het gehele getal n:
Gehele getallen mag ik buiten de functie g brengen volgens het inzicht van vergelijking (14):
De laatste stap is om links en rechts door n
2 te delen:
Aangezien de enige restrictie voor m en n is dat het gehele getallen zijn kan k ieder gewenst reëel getal zijn in de
limiet dat n naar oneindig gaat.
Oftewel, k is een willekeurig reëel getal.
Hiermee wordt vergelijking (10) equivalent aan:
De eerste regel van bovenstaande vergelijking samen met de tweede regel zijn de twee voorwaarden voor lineariteit.
Conclusie: de functie g is lineair.
Het verband tussen de functies f en g is ook lineair (zie vergelijking (9)) en daaruit volgt dan weer dat de
functie f eveneens lineair moet zijn en daarmee dan tevens de
Lorentz-transformaties (vergelijking (3)).
Een andere aanpak is de volgende.
Stel ik heb wederom een passerende waarnemer W’, met een constante snelheid v.
Op de een of andere manier kan ik de ruimtetijdcoördinaten voor W’ berekenen middels bepaalde transformatievergelijkingen.
Of anders gezegd, de ruimtetijdcoördinaten voor W’ zijn functies van de ruimtetijdcoördinaten t, x, y en z (voor een
waarnemer W) plus de snelheid v:
Ik heb op dit moment nog geen idee hoe deze vier functies eruit zien, ik weet alleen dat ze moeten bestaan.
De coördinaten x, y en z zijn puur wiskundige abstracties en de bijbehorende assen kan ik neerleggen zoals ik wil.
Voor het gemak (van wat komen gaat) leg ik de x-as en de x’-as in de richting van de snelheid.
Vervolgens leg ik een staaf op de x-as.
Het ene uiteinde ligt op x-coördinaat x
1 en het andere uiteinde op x-coördinaat x
2
(x
1 < x
2).
De bijbehorende x-coördinaten voor W’ zijn:
De lengte van de staaf is:
Ik kan de lengte van de staaf ook uitdrukken in de coördinaten van W’.
Dit wil
niet zeggen dat W’ het verschil van die twee coördinaten ook werkelijk kan en/of moet duiden als
de lengte van de staaf.
Het gaat puur en alleen om een uitdrukking in de coördinaten van W’ voor de lengte van de staaf zoals ik die in de
vorige vergelijking heb opgeschreven:
Vervolgens leg ik de staaf een eindje verderop en dat eindje noem ik ∆x.
Ik ga ervan uit dat het verleggen van de staaf geen invloed heeft op de lengte van de staaf, want ik neem immers
aan dat de ruimte homogeen is.
Ik schrijf wederom de lengte van de staaf op, zoals waargenomen door een waarnemer W bij de staaf (W is in rust ten
opzichte van de staaf) en W’:
Ik stel de vergelijkingen (22b) en (23b) aan elkaar gelijk:
Ik deel beide zijden door ∆x:
Vervolgens neem ik de limiet voor ∆x gaat naar nul, of anders gezegd, ∆x wordt infinitesimaal klein:
Wat ik hier heb staan zijn twee
afgeleiden,
links in het punt x = x
1 en rechts in het punt x = x
2:
Ik heb x
1 en x
2 volledig willekeurig gekozen en dat impliceert dat de
afgeleide van f
x naar x
altijd (voor iedere x) hetzelfde resultaat oplevert, oftewel een constante moet zijn.
Het directe gevolg daarvan is dat f
x een lineaire (eerstegraads) functie van x moet zijn.
Door in het voorgaande x, y en z cyclisch te verwisselen of met meerdere staven te werken volgt
daaruit dezelfde conclusie voor f
y en f
z en tevens dat het lineaire functies
van y en z moeten zijn.
Wat ik ook aanneem is dat gewoon even een tijdje wachten eveneens geen invloed heeft op de lengte van
de staaf, want dit hele verhaal rust op de aanname dat ruimtetijd homogeen is (dus zowel ruimte als tijd).
Op dezelfde manier zoals ik dat hiervoor heb gedaan met het ruimtelijk verplaatsen van de staaf kan ik
dat ook doen voor twee willekeurige tijdstippen.
Daaruit volgt dan dat de
afgeleide
van iedere functie f naar de tijd een constante moet zijn en dat iedere functie f een lineaire functie
van t moet zijn.
De transformatievergelijkingen (20) zijn dus lineaire vergelijkingen:
Tot slot nog het volgende.
Een zeer belangrijk ondersteunend argument waarom de transformatievergelijkingen lineair moeten zijn is de
eerste wet van Newton:
- een voorwerp waar geen krachten op worden uitgeoefend is in rust of beweegt zich met constante snelheid langs een
rechte lijn.
Als de vergelijkingen (28) geen lineaire vergelijkingen zouden zijn dan zou een voorwerp voor de ene waarnemer langs een
rechte lijn bewegen en voor een andere waarnemer niet, terwijl de waarnemers onderling met een constante snelheid bewegen.
Met andere woorden, voor de ene waarnemer wordt er geen kracht uitgeoefend op het voorwerp en voor de andere waarnemer wel.
Tenzij natuurlijk de eerste wet van Newton niet deugt.
Deze optie wil ik uiteraard niet uitsluiten, want het zou zeker niet de eerste keer zijn dat er in de natuurkunde een
overtuiging bij het grof vuil gezet moet worden waar men al eeuwen twijfelloos over was, maar vooralsnog is er tot op
heden geen enkele reden om aan te nemen dat de eerste wet van Newton niet de werkelijkheid beschrijft en aanpassing behoeft.
Daarnaast is het wel zo dat alleen de eerste wet van Newton als basis onvoldoende is.
Ik schrijf Newton’s eerste wet even uit in formulevorm (in alleen de x-richting):
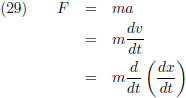
Stel nou dat zowel ruimte als tijd dezelfde afhankelijkheid hebben van een onbekende andere parameter:
In dit geval blijft de eerste wet van Newton overeind terwijl het voorgaande betoog in duigen valt.
De eerste wet van Newton is een belangrijk ondersteunend argument voor de lineariteit van de transformatievergelijkingen,
maar zeker geen bewijs.


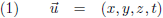
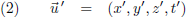
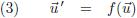
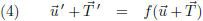
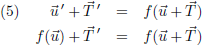
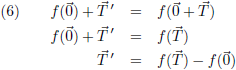
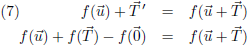
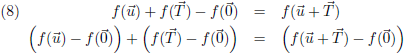
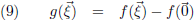
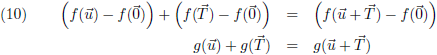
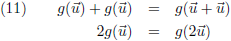
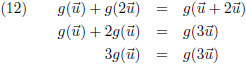
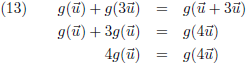
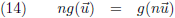
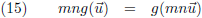
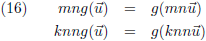
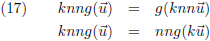
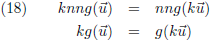
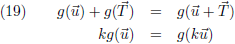
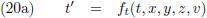
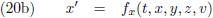
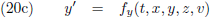
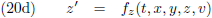
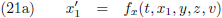
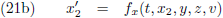
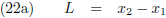
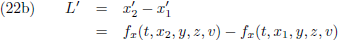
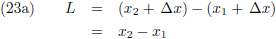
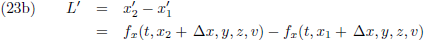
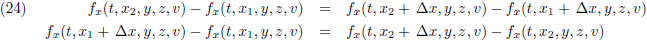
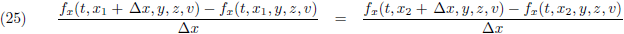
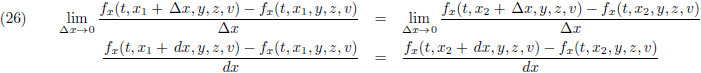
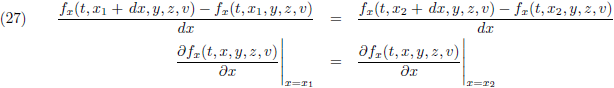
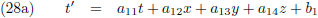
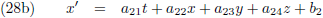
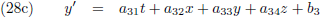
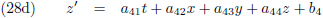
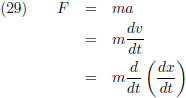
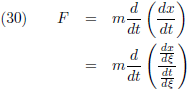


 Door naar het volgende vraagstuk: directe snelheid en reciproke snelheid
Door naar het volgende vraagstuk: directe snelheid en reciproke snelheid Terug naar het vorige vraagstuk: de maximale snelheid
Terug naar het vorige vraagstuk: de maximale snelheid Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De Lorentz-transformaties
De Lorentz-transformaties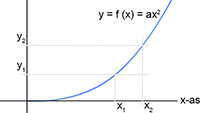 Differentiëren
Differentiëren Een oneindig groot oppervlak verven
Een oneindig groot oppervlak verven Christoffel-symbolen van de eerste soort bij een diagonale metriek
Christoffel-symbolen van de eerste soort bij een diagonale metriek Hoe vormt zich de Ricci-tensor?
Hoe vormt zich de Ricci-tensor? Wat geeft jouw leven betekenis?
Wat geeft jouw leven betekenis? De illusie van de angst
De illusie van de angst De reis naar de werkelijkheid van Barack Obama
De reis naar de werkelijkheid van Barack Obama De Natuur spreekt: The Soil/De Grond
De Natuur spreekt: The Soil/De Grond Wat is genoeg?
Wat is genoeg? De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van Vectoren
Vectoren Vectoren, vraagstuk 30
Vectoren, vraagstuk 30 Vectoren, vraagstuk 68
Vectoren, vraagstuk 68 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen