De transformatievergelijking voor versnelling
Leid op verschillende manieren de relativistische transformatievergelijking af voor versnelling.
Versnelling is gedefinieerd als snelheidsverandering per verstreken tijd.
Maar hoe ziet versnelling eruit relativistisch gezien?
Een waarnemer W
1 ziet een tweede waarnemer, W
2, voorbijkomen met een constante snelheid +v.
Waarnemer W
2 ziet W
1 daarom met een snelheid −v.
Op een bepaald moment, t
0 voor W
1, t
0' voor W
2, zet W
2 een
constante versnelling a' in gang.
Na een heel klein tijdje dt' is zijn snelheid een heel klein beetje dv' toegenomen:
W
1 zag eerst W
2 met een snelheid v en nu ziet hij hem met een iets hogere snelheid v + dv.
W
1 neemt een snelheidsverandering waar van dv en voor W
2 is dat dv'.
Vervolgens komt W
2 op het idee om de twee snelheden, zoals waargenomen door W
1,
relativistisch van elkaar af te trekken om zodoende een relatie te vinden tussen dv' en dv.
Want vanuit W
2 gezien moet het verschil dv, zoals waargenomen door W
1, via een
relativistische vertaalslag overeenkomen met zijn dv'.
Het
relativistisch optellen van snelheden
(of aftrekken, want dat is het optellen van een negatieve snelheid) gaat als volgt:
En daar maken we nu gebruik van:
Omdat dv infinitesimaal klein is
en daarom te verwaarlozen is ten opzichte van v gaat deze vergelijking over in (hierin is γ de
Lorentz-factor):
Oftewel, na combinatie met vergelijking (1):
Ik deel links en rechts door dt:

En versnellen maar!
Hoe nu verder?
Die breuk dt'/dt is een afgeleide,
een richtingscoëfficiënt
van een raaklijn, pure tijddilatatie,
oftewel een factor 1/γ.
Dan wordt vergelijking (6):
Ik kan ook netjes de
Lorentz-transformaties ter hand nemen:
Van vergelijking (8a) neem ik de
differentiaal:
Dit resultaat stop ik in vergelijking (6):
Die snelheid u' is
infinitesimaal klein
en daarom te verwaarlozen ten opzichte van v.
Zo kom ik wederom tot:
Ik kies weer een andere aanpak waarbij ik wederom gebruik maak het
relativistisch optellen van snelheden (hoe wordt een
snelheid u' waargenomen vanuit een ander stelsel dat met een snelheid v voorbij komt):
Ik bepaal de
differentiaal van u:
Door de vergelijkingen (9) en (13) te combineren krijg ik:
Alleen al uit het simpele feit dat dit consistent moet zijn met de vergelijkingen (7) en (11) volgt dat de
snelheid u'
infinitesimaal klein is
en daarom volledig wegvalt ten opzichte van v.
Hierdoor gaat (14) over in het inmiddels bekende resultaat:
Ik kan het nog anders bekijken door te stellen dat x' = 0 op het moment dat ik dit alles beschouw/waarneem
(daar is uiteraard helemaal niets op tegen als meebeweger).
De vergelijking (8a) wordt dan:
Ik bepaal wederom de
differentiaal:
Door dit te combineren met vergelijking (5) krijg ik nogmaals:
Zo ben ik op vier verschillende manieren tot hetzelfde resultaat gekomen:
Op ieder moment kan ik er een inertiaalstelsel bijzetten dat momentaan meebeweegt (met de nadruk op
momentaan!).
Heel netjes gezegd hebben we te maken met een momentaan meebewegend inertiaalstelsel
[Engels: momentarily comoving inertial frame, afgekort: MCIF].
Het meisje hiernaast is wellicht een aardige illustratie, want zij hangt natuurlijk niet echt zomaar
stil in de lucht te hangen.
De zwaartekracht werkt op haar in en er is dus echt wel versnelling aan het werk, maar het fototoestel
(de korte sluitertijd daarvan) fungeert als een soort momentaan meebewegend inertiaalstelsel.

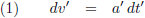
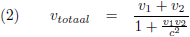
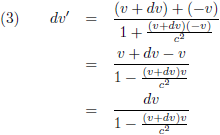
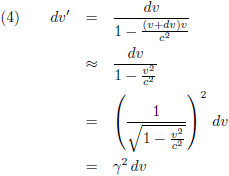
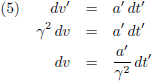
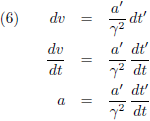

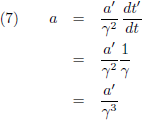
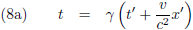
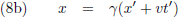
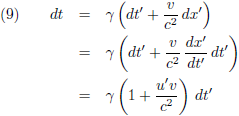
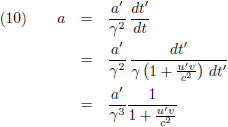
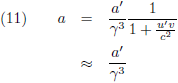
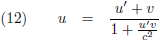
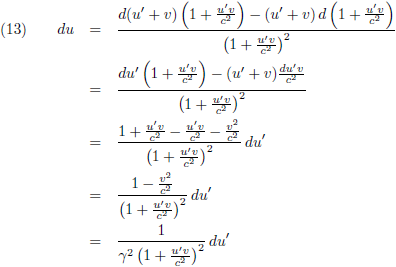
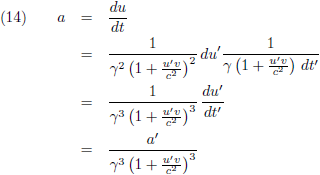
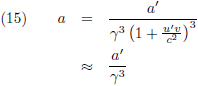
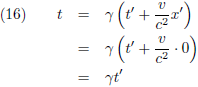
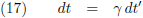
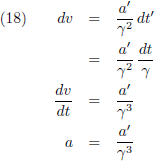



 Door naar het volgende vraagstuk: de magnetische kracht als relativistisch bijverschijnsel
Door naar het volgende vraagstuk: de magnetische kracht als relativistisch bijverschijnsel Terug naar het vorige vraagstuk: de transformatievergelijkingen voor krachten
Terug naar het vorige vraagstuk: de transformatievergelijkingen voor krachten Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 28
Vectoren, vraagstuk 28 Vectoren, vraagstuk 66
Vectoren, vraagstuk 66 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van Fourier-analyse
Fourier-analyse Relativiteitstheorie rekenkundig, hoofdstuk 2: de lichtsnelheid
Relativiteitstheorie rekenkundig, hoofdstuk 2: de lichtsnelheid Uitleg artikel precessie van Mercurius: inleiding
Uitleg artikel precessie van Mercurius: inleiding Relativistische periheliumprecessie, 2e orde benadering
Relativistische periheliumprecessie, 2e orde benadering De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat Fourier-analyse van het onzekerheidsprincipe van Heisenberg (I)
Fourier-analyse van het onzekerheidsprincipe van Heisenberg (I) De grote vragen in het leven
De grote vragen in het leven De illusie dat ik beter ben dan anderen
De illusie dat ik beter ben dan anderen De reis naar de werkelijkheid van Rolando Toro
De reis naar de werkelijkheid van Rolando Toro Klimaatverandering
Klimaatverandering Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen