Eddington-Finkelstein-coördinaten
In de eerste plaats zijn het eigenlijk Eddington-coördinaten, want hij schreef ze als eerste op (in 1924, toen was Finkelstein nog niet eens geboren) en Finkelstein kwam er pas veel later (in 1958) nogmaals mee aanzetten. Echter, door weer zo’n rare historische twist zijn de namen van beide heren nu verbonden aan dit coördinatenstelsel.
Goed, dat gezegd hebbende, Eddington-Finkelstein-coördinaten zijn een soort bolcoördinaten waarbij je de tijd t omzet als volgt: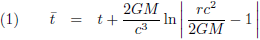
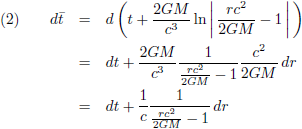
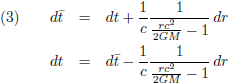
Het feit dat ik de tijdcoördinaat ga omzetten geeft eigenlijk al wel aan dat ik met relativiteitstheorie bezig ben. Daarom pak ik nu de Schwarzschild-oplossing erbij, de eerste en eenvoudigste oplossing van de vergelijkingen van de algemene relativiteitstheorie:
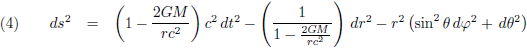
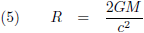
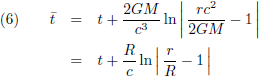
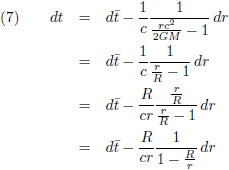
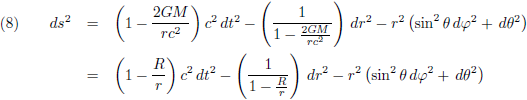
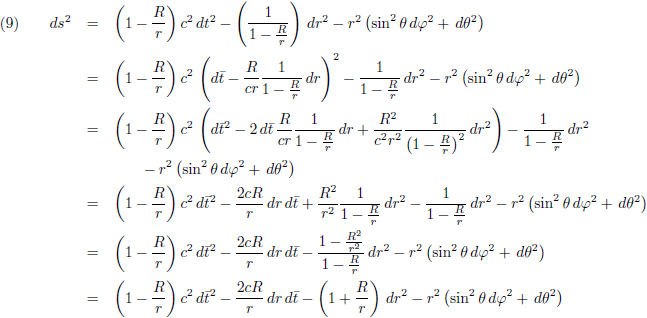
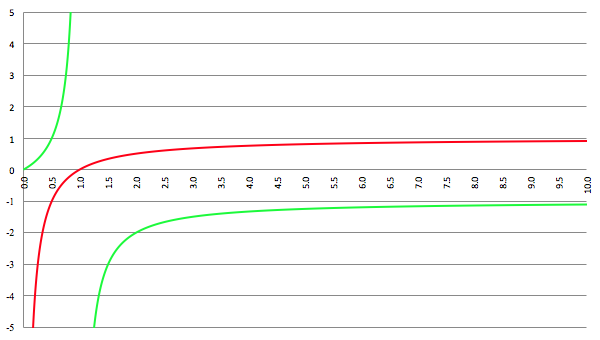
De grafiek van g00 (de rode lijn) en g11 (de groene lijn) in bolcoördinaten
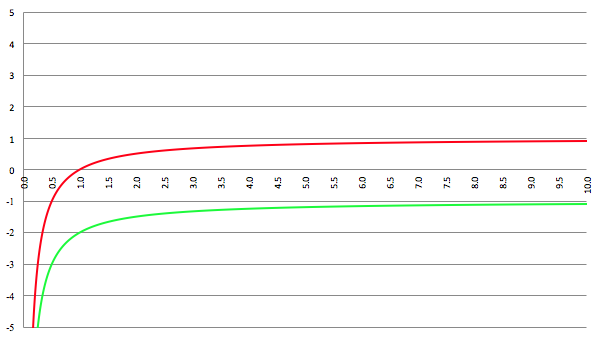
De grafiek van g00 (de rode lijn) en g11 (de groene lijn) in Eddington-Finkelstein-coördinaten
Er zijn nu geen wiskundige problemen meer in die zin dat een noemer op enig moment nul wordt. Behalve natuurlijk voor r = 0, maar dat was altijd al zo, ook bij de gravitatiewet van Newton:
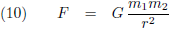
Dat brengt ons bij dit overzicht:
| De Schwarzschild-oplossing | |
| In bolcoördinaten | 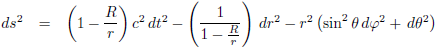 Toon afleiding |
| In Eddington-Finkelstein-coördinaten | 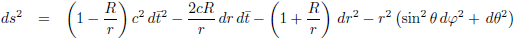 |
| In isotrope coördinaten | 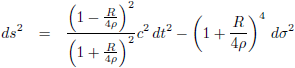 Toon afleiding |




 Door naar het volgende vraagstuk: Christoffel-symbolen van de Schwarzschild-metriek
Door naar het volgende vraagstuk: Christoffel-symbolen van de Schwarzschild-metriek Terug naar het vorige vraagstuk: relativistische periheliumprecessie, 2e orde benadering
Terug naar het vorige vraagstuk: relativistische periheliumprecessie, 2e orde benadering Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie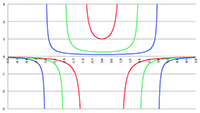 De integraal van
De integraal van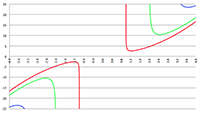 De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van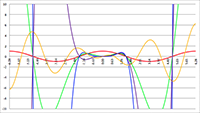 De integralen van
De integralen van Vectoren, vraagstuk 38
Vectoren, vraagstuk 38 Vectoren, vraagstuk 76
Vectoren, vraagstuk 76 Uitschrijven van de sommatieconventie
Uitschrijven van de sommatieconventie De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van De stelling van Green
De stelling van Green Uitleg artikel algemene relativiteitstheorie: voorpagina
Uitleg artikel algemene relativiteitstheorie: voorpagina Lijnen trekken door negen punten
Lijnen trekken door negen punten De transformatievergelijking voor versnelling
De transformatievergelijking voor versnelling Hemelmechanica
Hemelmechanica Het elektrische veld in een kooi van Faraday
Het elektrische veld in een kooi van Faraday Wanneer heb je voor het laatst iets nieuws gedaan?
Wanneer heb je voor het laatst iets nieuws gedaan? De illusie dat het goed gaat met mij
De illusie dat het goed gaat met mij Vertellingen
Vertellingen Reisverslag Georgië
Reisverslag Georgië Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen