De invariante lichtsnelheid en tijddilatatie
Laat zien dat het specifiek de invariante lichtsnelheid is die voor
tijddilatatie zorgt.
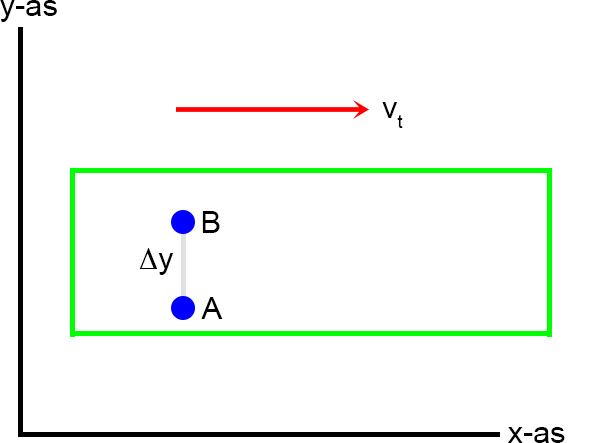
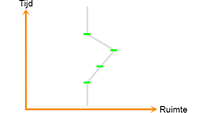
Een treinpassagier is met een balletje aan het spelen, het balletje rolt van A naar B:

De trein
De trein beweegt naar rechts met een snelheid vt maar daar merkt de passagier zelf helemaal niets van.
De trein, hijzelf, het balletje en alles wat zich in de trein bevindt bewegen zich allemaal met diezelfde snelheid vt naar rechts.
De waarneming dat de trein zich vooruit spoedt met een snelheid vt is een waarneming van iemand buiten de trein.
De passagier rolt het balletje naar de andere kant van de coupé (loodrecht op de bewegingsrichting) en de snelheid van het balletje noem ik vb.
Daarbij wordt een afstand AB afgelegd waarvoor geldt:
Oftewel:
En deze vergelijking ga ik links en rechts
kwadrateren met het oog op wat nog komen gaat:

De boer
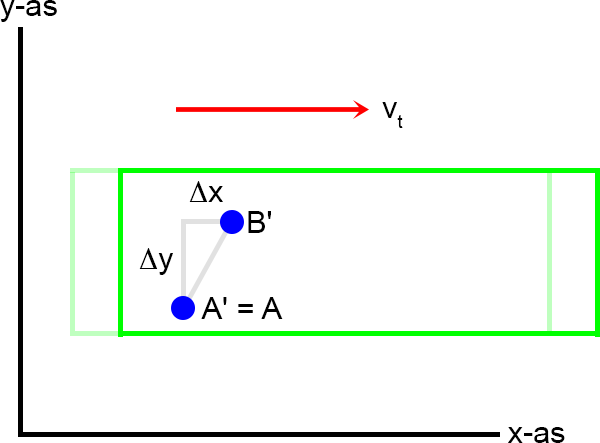
In het weiland staat een boer die de trein voorbij ziet komen.
Hij ziet ook de treinpassagier die met een balletje aan het spelen is:
Hij ziet dat de treinpassagier het balletje naar de andere zijde van de wagon rolt maar hij ziet tegelijkertijd dat de trein in diezelfde tijd een
stukje naar rechts opgeschoven is.
Vanuit zijn beleving heeft het balletje een afstand A'B' afgelegd waarvoor geldt
(met gebruikmaking van de stelling van Pythagoras):
Oftewel:
Er is één ding waarover de treinpassagier en de boer volledige overeenstemming zullen hebben: de afstand ∆y.
Daarom kan ik de belevingen van de treinpassagier en de boer middels (∆y)
2 aan elkaar koppelen als volgt:
Tot het jaar 1905 ging iedereen ervan uit dat de tijd gelijkmatig voortgaat voor alle bewoners van dit universum, dus ook voor de
treinpassagier en de boer:
Dan kunnen we de tijd gewoon uitdelen en houden we over:
De boer ziet een hogere snelheid van het balletje omdat vanuit zijn gezichtsveld de snelheid van de trein bijdraagt aan de snelheid van het balletje.
En inderdaad, wanneer de treinpassagier en de boer met behulp van wat apparatuur de snelheid van het balletje nameten vanuit hun beider
posities dan vinden zij waarden die perfect in overeenstemming zijn met bovenstaande vergelijking (ervan uitgaande dat hun apparatuur niet
nauwkeuriger is dan een stuk of tien cijfers achter de komma...).

De treinpassagier met de zaklamp
De treinpassagier is het spelen met het balletje zat en gaat met zijn zaklamp spelen.
Nu gaat het niet meer om een balletje maar om lichtstralen.
Met c als de snelheid van het licht verandert vergelijking (8) dan in:
De treinpassagier en de boer hebben echter wel zoveel kennis van natuurkunde dat ze weten dat de lichtsnelheid voor alle waarnemers gelijk is.
Met andere woorden:
Dit confronteert hen met het feit dat vergelijking (9) niet waar kan zijn.
De enige uitweg is om hun berekeningen nog eens grondig na te gaan en ze zullen moeten concluderen dat vergelijking (7) ook in twijfel
getrokken moet worden!
Ze hadden de tijd daarom
niet uit mogen delen en dat brengt hen terug bij:
Dit gecombineerd met (10) geeft:
Door te stellen dat:
Dan ontstaat:
Door ook nog te stellen dat:
Zo kom ik tenslotte tot:
De treinpassagier en de boer komen tot de conclusie dat de boer de tijdsvoortgang in de trein met een
factor γ ziet vertragen ten opzichte
van de tijdsvoortgang bij de boer:
tijddilatatie.
Maar door het hele verhaal om te draaien, namelijk de boer staat in het weiland met een zaklamp te spelen en de treinpassagier
ziet de boer met een snelheid v langskomen, komen ze tot de omgekeerde conclusie.
De treinpassagier ziet de tijdsvoortgang bij de boer met een
factor γ vertragen ten opzichte van de tijdsvoortgang in de trein.
Hoe onvoorstelbaar het ook is, ze zien
allebei de tijd bij de ander vertragen met dezelfde
factor γ en tevens lopen hun tijden
niet gelijk.
De Lorentz-factor γ heeft geen echte klassieke tegenhanger,
anders dan het getal één.
Klassiek is tijd immers gewoon tijd en dit gold ook nog voor een aantal andere zaken.
In de tabel met Taylor-reeksen vinden we:
Hiermee kan ik (1 − β
2)
1/2 ook schrijven als volgt:
Merk op dat de eerste term gelijk is aan de klassieke waarde en alle volgende termen zijn relativistische bijdragen
(die pas significant worden wanneer v in de buurt komt van c):
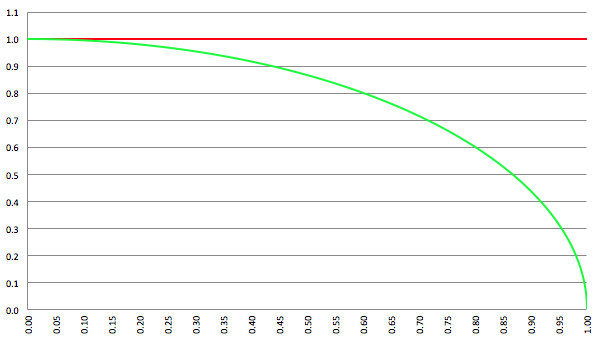
De grafiek van (1 − β
2)
1/2 (de groene lijn),
klassiek (de rode lijn) en relativistisch (de groene lijn)

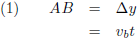
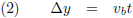
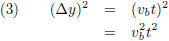

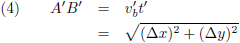
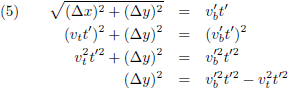
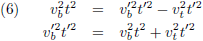
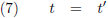
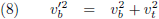

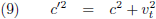
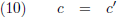
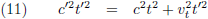
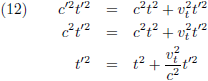
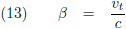
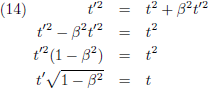
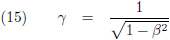
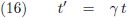
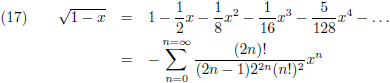
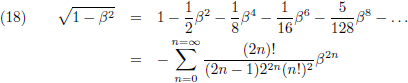




 Door naar het volgende vraagstuk: het tekenen van een wereldlijn
Door naar het volgende vraagstuk: het tekenen van een wereldlijn Terug naar het vorige vraagstuk: driedimensionale - en vierdimensionale snelheid
Terug naar het vorige vraagstuk: driedimensionale - en vierdimensionale snelheid Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie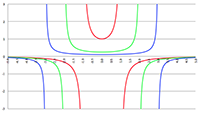 De integraal van
De integraal van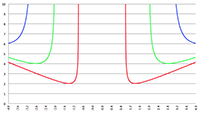 De integraal van
De integraal van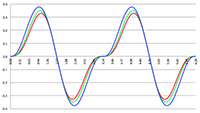 De integraal van
De integraal van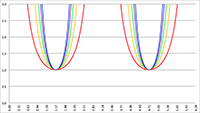 De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 37
Vectoren, vraagstuk 37 Vectoren, vraagstuk 75
Vectoren, vraagstuk 75 De sommatieconventie van Einstein
De sommatieconventie van Einstein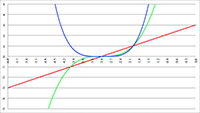 De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van De stelling van Green
De stelling van Green Uitleg artikel algemene relativiteitstheorie
Uitleg artikel algemene relativiteitstheorie De vrouw en haar spiegel
De vrouw en haar spiegel De transformatievergelijkingen voor krachten
De transformatievergelijkingen voor krachten Astronomie
Astronomie Vraagstukken elektriciteit en magnetisme
Vraagstukken elektriciteit en magnetisme Wanneer heb je voor het laatst écht iets meegemaakt?
Wanneer heb je voor het laatst écht iets meegemaakt? De illusie van gezond verstand
De illusie van gezond verstand Vertellingen
Vertellingen Once upon a time in the west: Geert Wilders
Once upon a time in the west: Geert Wilders Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen