Uitleg artikel algemene relativiteitstheorie: paragraaf 7
Trefwoorden: algemene relativiteitstheorie, Annalen der Physik, Die Grundlage der allgemeinen Relativitätstheorie/De grondslag van de algemene relativiteitstheorie, Königlich Preussischen Akademie der Wissenschaften/Koninklijke Pruisische Academie der Wetenschappen
Hoofdstuk B:
Wiskundige hulpmiddelen voor de opstelling van algemeen covariante vergelijkingen.
Paragraaf 7:
Vermenigvuldiging van tensoren.
Zoals de titel van deze paragraaf al aangeeft gaat Einstein het nu hebben over het vermenigvuldigen van tensoren.
En met de vorige paragraaf
nog helemaal vers in het geheugen (toch?) is dit waarschijnlijk een van de eenvoudigste paragrafen van het hele artikel.
Het is een direct vervolg op paragraaf 6,
maar dan inzichtverhogend (hoop ik).
Goed, het vermenigvuldigen van tensoren dus.
In paragraaf 6
vertelde ik al dat de Engelsen het tensor product aanduiden met outer product en hoe heet dit in het Duits?
Äuβere Multiplikation (dus net als in het Engels).
Wij gaan het ‘gewoon’ hebben over het tensor product.
Stel je hebt een tensor van rang a en een tensor van rang b, en die vermenigvuldig je met elkaar, dan krijg je als
uitkomst een tensor met rang a + b.
Tensoren vermenigvuldigen doe je door het dyadisch product te nemen en dit betekent: alle componenten
van de ene tensor stuk voor stuk vermenigvuldigen met alle componenten van de andere tensor.
Stel ik heb een tensor van de tweede rang:
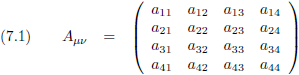
En een tensor van de eerste rang (een vector dus):
Vervolgens kan ik alle componenten van de tensor A
μν eerst met b
1 vermenigvuldigen, daarna met
b
2, dan met b
3 en tenslotte nog met b
4.
Op die manier krijg ik vier vlakken met componenten als volgt:
En als ik deze vier vlakken als vier plakken achter elkaar zet dan heb ik een kubus met componenten van de nieuw gevormde tensor T.
In formulevorm ziet dat er dan zo uit:
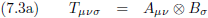
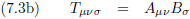 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
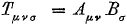
En ik kon het niet nalaten om toch één keer het symbool voor het tensor product erin te gooien.
Ook al wordt die nooit gebruikt, hij staat er wel!
Ik heb nu een covariante tensor (lage indices) en een covariante vector (lage index) gebruikt in dit voorbeeld, maar voor een
contravariante tensor (hoge indices) en een contravariante vector (hoge index) pakt dit natuurlijk net zo uit,
want het uitvoeren van de vermenigvuldiging gaat exact eender.
Tot en met drie rangen is een tensor nog te visualiseren als een kubus van getallen, maar voor hogere rangen werkt dit niet meer
(om stoer te doen heeft men het dan wel over een
hyperkubus, niemand weet wat het voorstelt maar het klinkt wel spannend).

Temperatuur wordt weergegeven middels een scalar, een tensor van de nulde rang
Het vermenigvuldigen van de componenten daarentegen verandert niet en het resultaat wordt dan (voor twee contravariante tensoren):
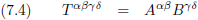 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
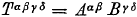
Het is uiteraard ook mogelijk om een covariante tensor en een contravariante tensor met elkaar te vermenigvuldigen.
Er ontstaat dan een gemengde tensor.
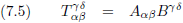 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
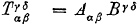
Einstein merkt nog op dat het bewijs, dat we hier als resultaat inderdaad een tensor hebben verkregen, volgt uit allerlei
vergelijkingen die in de
vorige paragraaf langsgekomen zijn.
Het bewijs komt uit de volgende vergelijkingen (hoe het tensor product van twee vectoren (tensoren van de eerste rang) een tensor
oplevert van de tweede rang):
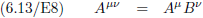 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

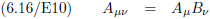 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

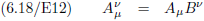 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Maar het is ook rechtstreeks te bewijzen uit de transformatieregels:
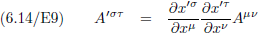 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
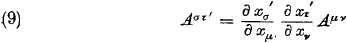
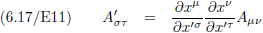 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

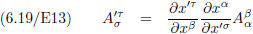 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
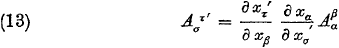
Eigenlijk verwijst hij naar de gehele
paragraaf 6
waar we de overstap hebben gemaakt van vectoren (tensoren van de eerste rang) naar ‘echte’ tensoren (rang 2 en hoger).

Snelheid wordt weergegeven middels een vector, een tensor van de eerste rang
Je kunt een tensor ook
verkleinen of, in de meest gangbare term, een
contractie uitvoeren
(Duits:
Verjüngung (verjongen), Engels:
contraction (contractie, samentrekking)).
Door een covariante index en een contravariante index aan elkaar gelijk te stellen vallen ze tegen elkaar weg en als gevolg
hiervan is dan de rang van de tensor 2 lager geworden.
Uiteraard kan dit alleen bij gemengde tensoren toegepast worden, omdat die zowel minstens één hoge index als één lage index hebben,
maar tegelijkertijd is het ook zo dat dit op
alle gemengde tensoren toegepast kan worden.
Laten we dit bijvoorbeeld eens toepassen op de tensor van vergelijking (7.5).
Eerst stellen we γ gelijk aan α:
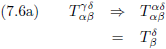 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
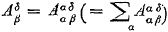
En vervolgens δ gelijk aan β:
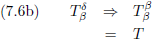 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
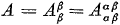
Merk op dat ik in dit voorbeeld twee keer achter elkaar de tensor verklein.
Ik begon met een tensor van de vierde rang, als tussenresultaat heb ik een tensor van de tweede rang, en ik eindig met een
tensor van de nulde rang (een getal).
Het bewijs komt voort uit de volgende vergelijkingen (en voor “invariant” kun je hier gewoon “getal” lezen):
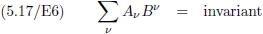 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
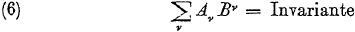
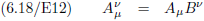 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:

Of uit de transformatieregel:
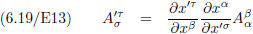 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
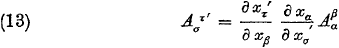
Er is uiteraard ook de mogelijkheid om naar hartelust te combineren.
Indien ik twee tensoren met elkaar vermenigvuldig (dyadisch product) en daarna het resultaat verklein (vooropgesteld dat het
resultaat een gemengde tensor is) ontstaat dit:
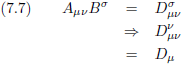 Oorspronkelijke vergelijkingen uit het artikel van Einstein:
Oorspronkelijke vergelijkingen uit het artikel van Einstein:
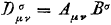
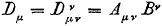
En Einstein noemt deze combi-bewerking
gemengde vermenigvuldiging, een kreet die je tegenwoordig
nergens meer tegenkomt (ik ben het in elk geval nooit ergens anders tegengekomen).
Hiervoor had ik een contravariante tensor van de eerste rang en een covariante tensor van de tweede rang,
maar ik kan natuurlijk ook uitgaan van twee tensoren van de tweede rang waarbij de ene tensor contravariant
en de andere tensor covariant is.
De verkleining kan dan ook twee keer uitgevoerd worden:
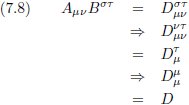 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
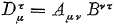
Hier doe ik hetzelfde als volgens vergelijking (7.6).
We borduren even voort op wat we net in vergelijking (7.8) gedaan hebben.
Uit twee tensoren A
μν en B
στ is uiteindelijk D voortgekomen.
D is een tensor van de nulde rang (geen indices), oftewel D is invariant, oftewel D is een scalar, oftewel D is een getal.
De omgekeerde redenering is ook geldig: indien D invariant is en B
στ is een tensor, dan
moet
A
μν ook een tensor zijn.
Stel we hebben een tensor A
μν die transformeert naar A
στ' en een tensor
B
μν die transformeert naar B
στ', dan geldt:
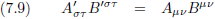 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
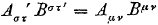
Er geldt ook:
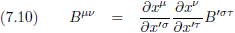 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
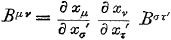
En als we dan vergelijking (7.10) in vergelijking (7.9) stoppen krijgen we:
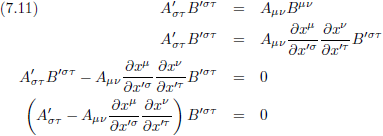 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
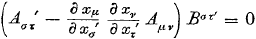
En hier staat hetzelfde als in vergelijking (6.17/E11), dus A is onmiskenbaar een tensor.
In dit voorbeeld is A een tensor van de tweede rang, maar dit geldt natuurlijk op analoge wijze voor een tensor van
iedere willekeurige rang.
In plaats van de tensor B
μν kun je ook twee vectoren
Cμ en
Dν neerschrijven, want die twee vectoren vormen middels het tensor product een nieuwe tensor
B
μν =
Cμ Dν.

Elektromagnetisme wordt weergegeven middels een tensor van de tweede rang
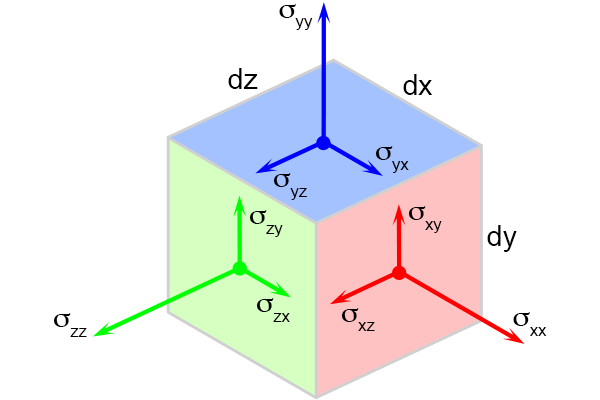
Mechanische spanning wordt weergegeven middels een tensor van de tweede rang

Vorm wordt weergegeven middels de metrische tensor, een tensor van de tweede rang
Einstein had het zojuist al over een gemengde vermenigvuldiging en nu noemt hij het wat algemener een
gemengde
operatie, want door te verkleinen neemt de rang van de tensor af en door het dyadisch product te nemen neemt de
rang van de tensor toe.
Enigszins vaag gesteld zorgen inwendig-achtige producten voor verlaging van rang en uitwendig-achtige producten (dyadisch)
voor een verhoging van rang.
STOP!
Hier maken we een hele belangrijke pas op de plaats.
Probeer datgene wat we tot nu toe in deze paragraaf gedaan hebben eens in grote lijnen te bekijken.
We zijn wel lekker bezig om tensoren met elkaar te ‘vermenigvuldigen’, maar ongemerkt hebben we twee fundamenteel
verschillende varianten op het tensor product.
Er zijn eigenlijk twee soorten tensor producten, er is een inwendige variant en een uitwendige variant.
Bij het
tensor inproduct doe ik iets inwendigs, de tensor keert in zichzelf, zijn rang daalt.
Dit herken ik doordat er gesommeerd wordt over een index, de dummy index.
Stel ik heb zoiets:
Hier staat eigenlijk:
Oftewel, voluit geschreven:
Kortom:
Door de rangen van de beide tensoren op te tellen en er dan twee vanaf te trekken voor iedere index waarover
gesommeerd wordt krijg je de rang van de resulterende tensor.
In dit voorbeeld: 1 + 1 − 2 = 0 (een scalar).
Indien er ergens een index tweemaal voorkomt dan moet er over die index gesommeerd worden (sommatieconventie
van Einstein).
Dus indien tweemaal dezelfde index aanwezig is:
- dan betekent dat: sommeren over die index,
- dan betekent dat: ‘iets inwendigs doen’,
- dan betekent dat: het tensor inproduct uitvoeren,
- dan betekent dat: twee omlaag in rang,
- dan betekent dat: dat er eigenlijk een ∙ (punt) staat tussen de tensoren die deelnemen
aan de bewerking,
- dan betekent dat: dat de punt weggelaten wordt omdat die geen informatie meer toevoegt,
- dan betekent dat ook dat een tensor-beginneling al heel snel de weg kwijt is helaas.
Indien je dus een index
wel tweemaal ziet staan in een tensorvergelijking, dan
moet je proberen de punten
die hierboven staan in een flits door je grijze massa te laten gaan.
En naast de inwendige variant is er dus ook de uitwendige variant, het
tensor uitproduct.
Bij het tensor uitproduct doe ik iets uitwendigs, de tensor keert zich naar buiten, hij explodeert,
zijn rang stijgt.
Dit herken ik doordat er
geen index tweemaal voorkomt.
Stel ik heb zoiets:
Oftewel, uitgeschreven in componenten:
Kortom:
Door de rangen van de beide tensoren op te tellen krijg je de rang van de resulterende tensor.
In dit voorbeeld: 1 + 1 = 2.
Indien geen enkele index tweemaal voorkomt dan moet er dyadisch vermenigvuldigd worden.
Dus indien
niet tweemaal dezelfde index aanwezig is:
- dan betekent dat: alle componenten dyadisch vermenigvuldigen,
- dan betekent dat: ‘iets uitwendigs doen’,
- dan betekent dat: het tensor uitproduct uitvoeren,
- dan betekent dat: omhoog in rang,
- dan betekent dat: dat er eigenlijk een
 (dyade)
staat tussen de tensoren die deelnemen aan de bewerking,
(dyade)
staat tussen de tensoren die deelnemen aan de bewerking,
- dan betekent dat: dat de dyade weggelaten wordt omdat die geen informatie meer toevoegt,
- dan betekent dat ook dat een tensor-beginneling al heel snel de weg (weer) kwijt is helaas.
Indien je dus een index
niet tweemaal ziet staan in een tensorvergelijking, dan
moet je proberen de punten
die hierboven staan in een flits door je grijze massa te laten gaan.

Kromming wordt weergegeven middels een tensor van de vierde rang
Nu pakken we de draad van het artikel weer op en ik zet vergelijking (7.11) hier weer neer die ik voor dit intermezzo
ook al had neergeschreven.
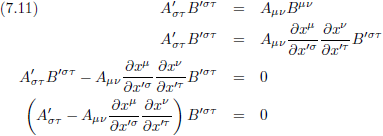 Oorspronkelijke vergelijking uit het artikel van Einstein:
Oorspronkelijke vergelijking uit het artikel van Einstein:
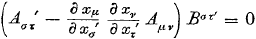
In plaats van de tensor B
μν kun je ook twee vectoren C
μ en
D
ν opschrijven, en voor B
στ' de vectoren C
σ'
en D
τ'.
Maar wat nou als de vectoren
C en
D dezelfde vectoren zijn?
Als ik hierboven kijk dan zie ik dat er aan het gedeelte dat tussen haakjes staat niets verandert of ik nou de
tensor B in de vergelijking zet of de vectoren
C en
D.
Echter, indien
C en
D dezelfde vectoren zijn, dan mag ik ook de indices μ en ν verwisselen
want de μ
e component van de ene vector vermenigvuldigen met de ν
e component van
de andere vector is gelijk aan de ν
e component vermenigvuldigen met de μ
e component.
En daar volgt dan uit dat A
μν = A
νμ, oftewel, A is een covariante
symmetrische tensor (zoals we al gezien hebben in
paragraaf 4 met de metrische tensor g).
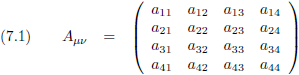
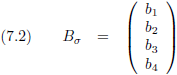




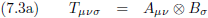
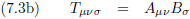
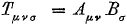

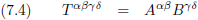
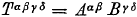
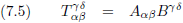
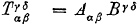
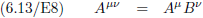

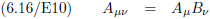

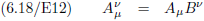

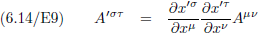
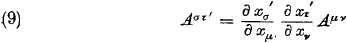
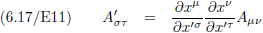

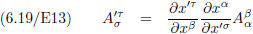
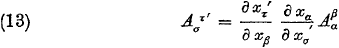

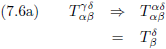
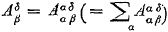
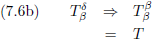
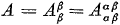
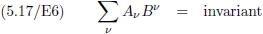
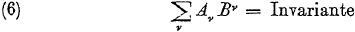
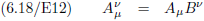

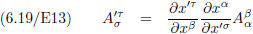
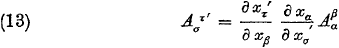
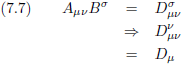
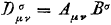
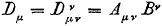
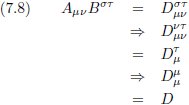
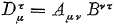
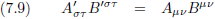
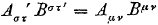
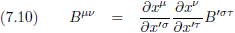
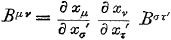
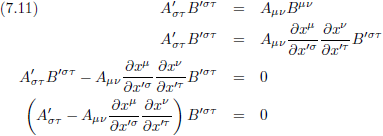
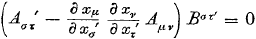



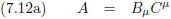
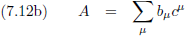
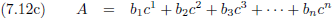
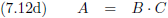
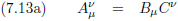
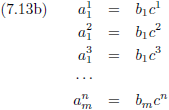
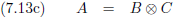
 (dyade)
staat tussen de tensoren die deelnemen aan de bewerking,
(dyade)
staat tussen de tensoren die deelnemen aan de bewerking,
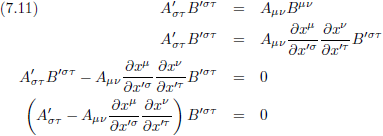
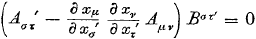

 Door naar de uitleg van de volgende paragraaf: paragraaf 8
Door naar de uitleg van de volgende paragraaf: paragraaf 8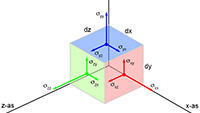 Terug naar de uitleg van de vorige paragraaf: paragraaf 6
Terug naar de uitleg van de vorige paragraaf: paragraaf 6 Naar de overzichtspagina van het artikel
Naar de overzichtspagina van het artikel Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 18
Vectoren, vraagstuk 18 Vectoren, vraagstuk 56
Vectoren, vraagstuk 56 Vectoren, vraagstuk 94
Vectoren, vraagstuk 94 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 1: snelheden
Relativiteitstheorie basic, hoofdstuk 1: snelheden Uitleg artikel algemene relativiteitstheorie: paragraaf 16
Uitleg artikel algemene relativiteitstheorie: paragraaf 16 De relativistische bewegingsvergelijkingen
De relativistische bewegingsvergelijkingen Leid de energie-impuls-relatie af
Leid de energie-impuls-relatie af Het modelleren van de dichtheid van de Zon
Het modelleren van de dichtheid van de Zon Vraagstukken algemene natuurkunde
Vraagstukken algemene natuurkunde De illusie dat dit een rechtvaardige wereld is
De illusie dat dit een rechtvaardige wereld is Reizigers naar de werkelijkheid
Reizigers naar de werkelijkheid Vorm en angst
Vorm en angst Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen