Uitleg artikel E = mc2
 (Credits voor de achtergrondfoto: NASA)
(Credits voor de achtergrondfoto: NASA)
Medio 1905 komt Einstein met zijn artikel waarin hij de speciale relativiteitstheorie uiteen zet.
In het najaar van 1905 publiceert hij vervolgens een kort artikel waarin hij nog een “interessant gevolg” van die speciale
relativiteitstheorie uit de doeken doet.
Het is een kort artikel van maar drie kantjes, maar met verstrekkende implicaties.
De beroemdste natuurkundige formule van de wereld, E = mc2, ziet hiermee het levenslicht terwijl deze formule in
het artikel helemaal niet voorkomt!
Een bijzondere historische curiositeit.
Hoe is Einstein aan zijn formule gekomen?
Dat spoor gaan we hier terug volgen.
Oftewel: E = mc2 volgens de meester.
Daartoe beginnen we bij het artikel van Einstein waarin hij de speciale relativiteitstheorie uiteenzet, want daarin zet hij een
vergelijking klaar die we verderop nodig hebben.
Dat artikel heet
Zur Elektrodynamik bewegter Körper (Over de elektrodynamica van bewegende lichamen).
- Geïnteresseerd in het oorspronkelijke artikel?
Stuur mij dan een email (karel@voorbijeinstein.nl)
met als onderwerp “PDF bestand 020103000000” en ik stuur je de file (gratis) toe.
Ik ga hier niet het hele artikel over de speciale relativiteitstheorie doorwerken, maar ik ga er even in vogelvlucht doorheen en ik
pak datgene eruit wat hier van belang is.
In de inleiding van het artikel verbaast Einstein zich erover dat het verschijnsel van een stroom die opgewekt wordt in een spoel op
twee totaal verschillende manieren beschreven en verklaard wordt.
Je kunt een magneet naar de spoel bewegen of je kunt de spoel naar de magneet bewegen, beide bewegingen wekken een spanning op aan
de uiteinden van de spoel en indien er sprake is van een gesloten stroomkring gaat er een elektrische stroom lopen.
Voor Galileï en Huygens was het reeds volkomen duidelijk dat mechanische beweging niet in absolute zin bestaat en Einstein zegt dat
dit kennelijk ook voor elektromagnetisme moet gelden en zet daarmee de ether definitief bij het grof vuil.
In de eerste - en tweede paragraaf van het artikel bespreekt hij
gelijktijdigheid,
en daaruit blijkt dat absolute gelijktijdigheid niet bestaat maar is gekoppeld aan de waarnemer.
Wat gelijktijdig is voor de één is niet gelijktijdig voor een ander en vice versa.
Dit is de conclusie die Einstein trekt aan het einde van paragraaf twee.
De derde paragraaf besteedt Einstein aan het afleiden van de Lorentz-transformaties.
Tijd en ruimte in twee stelsels, P en Q, die met een snelheid v ten opzichte van elkaar bewegen (in de x-richting) zijn als volgt in
elkaar om te rekenen:
Hierin is de
Lorentz-factor γ:
Lorentz had deze transformaties afgeleid in het licht van (leuke woordspeling) de vergelijkingen van Maxwell, maar Einstein zet ze hier in
een veel breder perspectief.
In paragraaf vier bespreekt Einstein vervolgens de verschijnselen
tijddilatatie en
lengtecontractie:
De vijfde paragraaf gaat over het
optellen van snelheden,
met dit als resultaat (wederom voor twee stelsels, P en Q):
Daarna laat Einstein de mechanica achter zich en stort zich op de wetten van Maxwell: het elektromagnetisme.
De beschouwingen in paragraaf zes laten zien dat de wetten van Maxwell onveranderd blijven na een
Lorentz-transformatie
(dit was immers ook waar Lorentz naar op zoek was dus dit is vanzelfsprekend).
Met al dit gereedschap (alle bovenstaande vergelijkingen) tot zijn beschikking gebruikt Einstein
de resterende paragrafen van het artikel (zeven, acht, negen en tien) om een aantal praktische verschijnselen
(het
Doppler-effect, aberratie, lichtenergie, stralingsdruk, convectiestromen
en de beweging van elektronen) door te rekenen.
Twee daarvan, het
Doppler-effect en lichtenergie
(hoe
elektromagnetische energie transformeert), hebben we ook nog nodig.
Het klassieke Doppler-effect voor een bewegende waarnemer is:
En voor een bewegende bron:
Einstein komt met één vergelijking voor het relativistische
Doppler-effect:
Voor lage snelheden wordt γ ≈ 1 en komt vergelijking (6) overeen met de vergelijkingen (5).
Wat we ook nog nodig hebben is de energie die besloten ligt in het elektromagnetische veld.
De
energie-inhoud van het elektrische veld (in vacuüm, per volume-eenheid) is:
En de
energie-inhoud van het magnetische veld (in vacuüm, per volume-eenheid) is:
De energie-inhoud van het elektromagnetische veld (in vacuüm, per volume-eenheid) is de som van deze twee energieën:
De essentiële vraag die Einstein hier beantwoord wilde hebben was hoe deze elektromagnetische energie door verschillende
waarnemers wordt waargenomen.
Na het nodige rekenwerk komt hij met de
transformatievergelijking voor elektromagnetische energie:
Deze vergelijking is het uitgangspunt van het artikel van Einstein waarin hij E = mc
2 afleidt, die moesten we dus
eerst leren begrijpen om Einstein verderop te kunnen volgen.
Op woensdag 27 september 1905 valt het artikel van Einstein, waarin hij zijn wereldberoemde formule uit de doeken doet,
bij de redactie van het Duitse wetenschappelijke tijdschrift
Annalen der Physik op de deurmat.
Het artikel heet
Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?
(
Is de traagheid van een lichaam van zijn energie-inhoud afhankelijk?).
- Geïnteresseerd in het oorspronkelijke artikel?
Stuur mij dan een email (karel@voorbijeinstein.nl)
met als onderwerp “PDF bestand 020103000000” en ik stuur je de file (gratis) toe.
Grappig genoeg wordt dé formule in het artikel helemaal niet genoemd.
Hieronder volgt een exacte weergave van dat artikel.
Ik heb dit prachtige stukje wetenschappelijke geschiedenis letterlijk overgenomen inclusief de symbolen die Einstein hanteert,
de lichtsnelheid is V en energie duidt hij aan met E, H, K, l of L.
Daar gaan we:
Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?
von A. Einstein.
Die Resultate einer jüngst in diesen Annalen von mir publizierten elektrodynamischen Untersuchung führen zu einer sehr interessanten
Folgerung, die hier abgeleitet werden soll.
Ich legte dort die Maxwell-Hertzschen Gleichungen für den leeren Raum nebst dem Maxwellschen Ausdruck für die elektromagnetische
Energie des Raumes zugrunde und auβerdem das Prinzip: Die Gesetze, nach denen sich die Zustände der physikalischen Systeme
ändern, sind unabhängig davon, auf welches von zwei relativ zueinander in gleichförmiger Parallel-Translationsbewegung befindlichen
Koordinatensystemen diese Zustandsänderungen bezogen werden (Relativitätsprinzip).
Gestützt auf diese Grundlagen leitete ich unter anderem das nachfolgende Resultat ab: Ein System von ebenen Lichtwellen besitze,
auf das Koordinatensystem (x, y, z) bezogen, die Energie l; die Strahlrichtung (Wellennormale) bilde den Winkel φ mit der
x-Achse des Systems.
Führt man ein neues, gegen das System (x, y, z) in gleichförmiger Paralleltranslation begriffenes Koordinatensystem
(ξ, η, ζ) ein, dessen Ursprung sich mit der Geschwindigkeit v längs der x-Achse bewegt, so besitzt die genannte
Lichtmenge - im System (ξ, η, ζ) gemessen - die Energie:
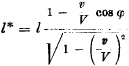
wobei V die Lichtgeschwindigkeit bedeutet.
Von diesem Resultat machen wir im folgenden Gebrauch.
Es befinde sich nun im System (x, y, z) ein ruhender Körper, dessen Energie - auf das System (x, y, z) bezogen - E
0 sei.
Relativ zu dem wie oben mit der Geschwindigkeit v bewegten System (ξ, η, ζ) sei die Energie des Körpers H
0.
Dieser Körper sende in einer mit der x-Achse den Winkel φ bildenden Richtung ebene Lichtwellen von der Energie L/2
(relativ zu (x, y, z) gemessen) und gleichzeitig eine gleich groβe Lichtmenge nach der entgegengesetzten Richtung.
Hierbei bleibt der Körper in Ruhe in bezug auf das System (x, y, z).
Für diesen Vorgang muβ das Energieprinzip gelten und zwar (nach dem Prinzip der Relativität) in bezug auf beide
Koordinatensysteme.
Nennen wir E
1 bez. H
1 die Energie des Körpers nach der Lichtaussendung relativ zum System (x, y, z)
bez. (ξ, η, ζ) gemessen, so erhalten wir mit Benutzung der oben angegebenen Relation:
Durch Subtraktion erhält man aus diesen Gleichungen:
Die beiden in diesem Ausdruck auftretenden Differenzen von der Form H - E haben einfache physikalische Bedeutungen.
H und E sind Energiewerte desselben Körpers, bezogen auf zwei relativ zueinander bewegte Koordinatensysteme, wobei der Körper in dem
einen System (System (x, y, z)) ruht.
Es ist also klar, daβ die Differenz H - E sich von der kinetischen Energie K des Körpers in bezug auf das andere System
(System (ξ, η, ζ)) nur durch eine additive Konstante C unterscheiden kann, welche von der Wahl der willkürlichen
additiven Konstanten der Energien H und E abhängt.
Wir können also setzen:
da C sich während der Lichtaussendung nicht ändert.
Wir erhälten also:
Die kinetische Energie des Körpers in bezug auf (ξ, η, ζ) nimmt infolge der Lichtaussendung ab, und zwar um einen von
den Qualitäten des Körpers unabhängigen Betrag.
Die Differenz K
0 - K
1 hängt ferner von der Geschwindigkeit ebenso ab wie die kinetische Energie des Elektrons.
Unter Vernachlässigung von Gröβen vierter und höherer Ordnung können wir setzen:
Aus dieser Gleichung folgt unmittelbar: Gibt ein Körper die Energie L in Form von Strahlung ab, so verkleinert sich seine Masse um
L/V
2.
Hierbei ist es offenbar unwesentlich, daβ die dem Körper entzogene Energie gerade in Energie der Strahlung übergeht, so
daβ wir zu der allgemeineren Folgerung geführt werden: Die Masse eines Körpers ist ein Maβ für dessen Energieinhalt;
ändert sich die Energie um L, so ändert sich die Masse in demselben Sinne um L/9 ∙ 10
20, wenn die Energie in Erg
und die Masse in Grammen gemessen wird.
Es ist nicht ausgeschlossen, daβ bei Körpern, deren Energieinhalt in hohem Maβe veränderlich ist (z. B. bei den
Radiumsalzen), eine Prüfung der Theorie gelingen wird.
Wenn die Theorie den Tatsachen entspricht, so überträgt die Strahlung Trägheit zwischen den emittierenden und absorbierenden
Körpern.
Bern, September 1905.
(Eingegangen 27. September 1905.)
Dit is de eerste vergelijking van Einstein:
Deze komt overeen met onze vergelijking (10), met dit verschil dat Einstein er ook nog een cos φ in heeft staan.
Wij zijn telkens uitgegaan van relatieve beweging in de x-richting en Einstein heeft dat wat algemener opgepakt.
Door de cos φ toe te voegen neemt hij de x-component van de snelheid en zit hij weer op ons pad.
Vanaf nu gaan we ervan uit dat de hoek φ = 0 en cos φ = 1.
Er is een referentiestelsel met (x, y, z) als coördinaten en een stelsel dat ten opzichte hiervan met een snelheid +v beweegt
en als coördinaten (ξ, η, ζ) heeft.
In het x-y-z-stelsel bevindt zich een voorwerp in rust ten opzichte van dit stelsel.
De energie van dit voorwerp is E
0 voor x-y-z-waarnemers en de energie van het voorwerp is H
0 voor
ξ-η-ζ-waarnemers.
Op een bepaald moment zendt het voorwerp licht uit in de +x-richting met energie L/2 en
tegelijkertijd eenzelfde
hoeveelheid licht in de −x-richting.
Nadat het licht uitgezonden is heeft het voorwerp een hoeveelheid energie gelijk aan E
1 voor x-y-z-waarnemers en
H
1 voor ξ-η-ζ-waarnemers.
Voor de x-y-z-waarnemers geldt:
Nu komt vergelijking (10) in actie want de ξ-η-ζ-waarnemers zeggen:
Deze twee laatste vergelijkingen trekken we van elkaar af:
Vervolgens zegt Einstein dat E en H betrekking hebben op de energie-inhoud van hetzelfde voorwerp waargenomen vanuit twee
verschillende referentiestelsels.
In het ene stelsel is het voorwerp in rust en in het andere stelsel is het voorwerp in beweging, dus het verschil tussen
E en H is de
kinetische energie (bewegingsenergie) K van het
voorwerp plus een willekeurige constante C:
Deze twee vergelijkingen vullen we in in (14):
Voor lage snelheden (snelheden ‘behoorlijk lager’ dan de lichtsnelheid, en dat is nagenoeg altijd het geval) kunnen we stellen dat:
En dit is de laatste vergelijking van het artikel van Einstein!
Niks E = mc
2, dat mag de lezer er zelf nog ‘even’ uithalen en dat gaan we natuurlijk doen.
Volgens de klassieke mechanica geldt voor de
kinetische energie:
Uit de combinatie van (18) en (19) volgt:
Of in de moderne, overbekende, notatie is die daar dan eindelijk:
Quod erat demonstrandum.
Wat hebben we hier nou aan?
De letter c staat voor de lichtsnelheid en snelheden drukken we normaliter uit in meters-per-seconde.
Bovendien is de lichtsnelheid een natuurconstante en als we ooit, in een ver verleden, de eenheid meter en de eenheid seconde anders
hadden gekozen dan had het zomaar kunnen zijn dat c = 1 m/s.
Echter, zo is het niet gegaan, en daarom is c in ons huidige eenhedenstelsel 299792458 m/s.
Maar stel nou dat c wel gelijk zou zijn aan één (puur een kwestie van afspraak), dan is c
2 ook gelijk aan één (want één
maal één is één).
Vergelijking (21) zou dan simpelweg worden: E = m.
Of voluit geschreven: energie = massa.
Anders gezegd: energie is een verschijningsvorm van massa en massa is een verschijningsvorm van energie.
Ruim honderd jaar geleden was dat een wereldontdekking en tegenwoordig is het nog steeds moeilijk te bevatten.
We hebben hierboven de afleiding van Einstein gevolgd, maar een alternatieve route is middels de
elastische botsing van twee ballen.
Wie het weet mag het zeggen, wat is de betere of handiger methode?
De botsing van de twee balletjes of de route van Einstein?
De twee balletjes hebben een volkomen elastische botsing hetgeen niet realistisch is, maar het voorwerp van Einstein moet volkomen
star zijn om het in rust te houden en dat is ook niet realistisch.
Bij de botsing van de twee balletjes nemen we de limiet dat de snelheid naar nul gaat, maar bij Einstein levert de gelijktijdigheid
problemen op tenzij je de limiet neemt dat het voorwerp een dikte van nul heeft.
Kortom, beide routes hebben discutabele limietovergangen.
Ik sta open voor alternatieven!
In de literatuur opent men heel vaak met:
Sorry, maar dan is de route al voor 90% afgelegd dus dat telt niet.
Een andere veelgebruikte route maakt gebruik van het volgende.
De impuls (massa maal snelheid) van een foton is:
Omdat m = E/c
2 geldt:
Deze formule wordt ook vaak als uitgangspunt gebruikt.
Sorry, maar dan gebruik je indirect het resultaat om het resultaat af te leiden dus dat telt ook niet.

Ontploffing van de atoombom boven Nagasaki
Doorgaans wordt E = mc2 in verband gebracht met nucleaire bommen ...
... kernreactoren ...

De Zon
(Credits: NASA)
... en het kernfusieproces dat sterren doet schijnen.
Dit zijn inderdaad de uitgesproken voorbeelden waar duidelijk wordt hoeveel energie er vertegenwoordigd wordt door een relatief
kleine hoeveelheid massa.
Bovendien levert het ook nog spectaculaire beelden op, en dat is voor de moderne mens met zijn/haar saaie en geestdodende leefomgeving
heel belangrijk (wanneer heb jij voor het laatst écht iets meegemaakt
of iets gedaan dat je nog nooit gedaan had?).
Terwijl, E = mc
2 is overal.
Op
deze pagina geef ik meer voorbeelden.

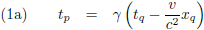
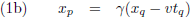
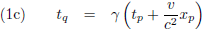
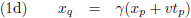
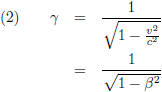
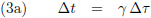
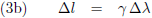
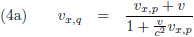
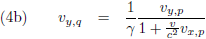
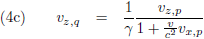
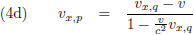
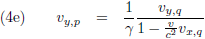
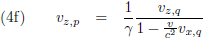
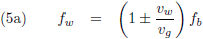
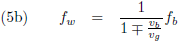
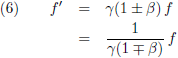
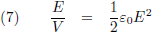
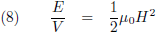
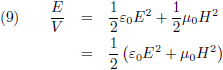
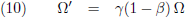

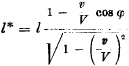
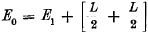
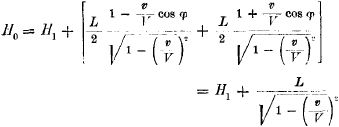
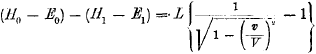
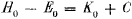
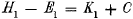
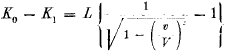
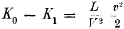
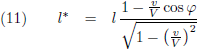
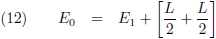
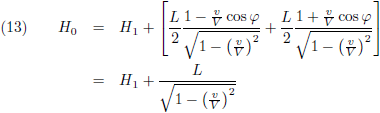
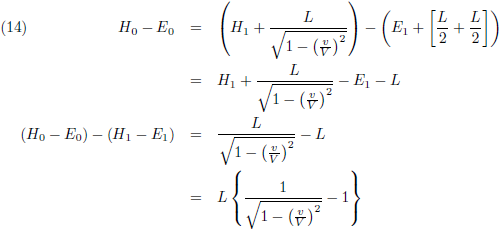
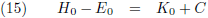
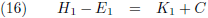
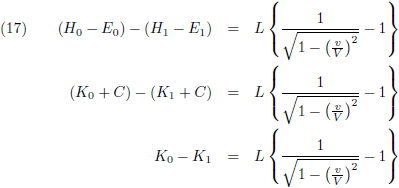
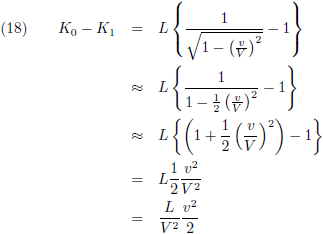
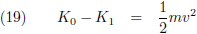
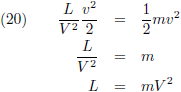
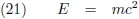
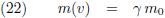
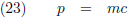
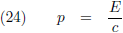









 Naar de overzichtspagina relativiteitstheorie
Naar de overzichtspagina relativiteitstheorie De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van Combinaties en manipulaties met nabla
Combinaties en manipulaties met nabla Vectoren, vraagstuk 37
Vectoren, vraagstuk 37 Vectoren, vraagstuk 75
Vectoren, vraagstuk 75 De sommatieconventie van Einstein
De sommatieconventie van Einstein De Taylor-reeks van
De Taylor-reeks van De Taylor-reeksen van
De Taylor-reeksen van De stelling van Green
De stelling van Green Uitleg artikel algemene relativiteitstheorie
Uitleg artikel algemene relativiteitstheorie De vrouw en haar spiegel
De vrouw en haar spiegel De transformatievergelijkingen voor krachten
De transformatievergelijkingen voor krachten Astronomie
Astronomie Vraagstukken elektriciteit en magnetisme
Vraagstukken elektriciteit en magnetisme Wanneer heb je voor het laatst écht iets meegemaakt?
Wanneer heb je voor het laatst écht iets meegemaakt? De illusie van gezond verstand
De illusie van gezond verstand Vertellingen
Vertellingen Once upon a time in the west: Geert Wilders
Once upon a time in the west: Geert Wilders Reacties op lezingen
Reacties op lezingen LaTeX
LaTeX Python code
Python code Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen