De trompet van Torricelli
De trompet van Torricelli is een bijzondere figuur, omdat het enerzijds eindige kenmerken heeft en anderzijds
oneindige kenmerken.
Ik ga de trompet construeren als volgt.
De opening van de trompet maak ik twintig centimeter breed, dus dit is het vooraanzicht van de trompet:
Verder maak ik de trompet zo dat de diameter van de trompet iedere tien centimeter evenredig kleiner wordt.
De voorkant van de trompet, de opening, is twintig centimeter breed, na tien centimeter de helft
(= 10 centimeter), na nogmaals tien centimeter een derde (= 6.67 centimeter), enzovoort.
Van opzij ziet de trompet er dan zo uit:
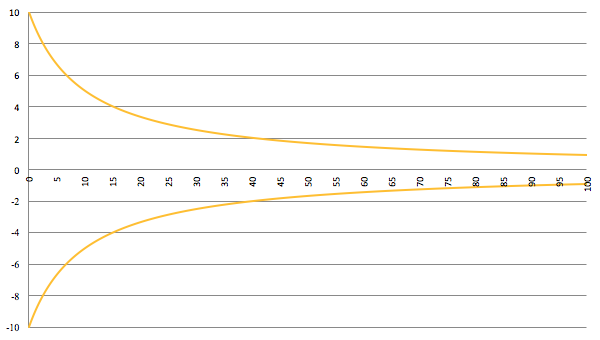
De eerste meter van de trompet
Wat is nou het bijzondere aan deze trompet?
Naarmate ik de trompet langer maak wordt het oppervlak van de trompet steeds groter, dat is logisch.
Echter, het volume blijft
niet alsmaar toenemen, maar bereikt een maximum.
De vorm van de trompet voldoet aan de volgende vergelijking (voor het gemak in decimeters):
Door deze functie om de x-as te wentelen vormt zich een omwentelingslichaam.
Het oppervlak van dit omwentelingslichaam is (L is de lengte van de trompet, en L = 0 bij x = 1):
Voor het oplossen van deze
integraal
heb ik gebruik gemaakt van de
tabel met integralen.
Het volume van dit omwentelingslichaam is:
De limietovergangen voor L gaat naar oneindig zijn:
De trompet heeft een oneindige lengte en een oneindig oppervlak, maar het volume is eindig.
Hoe bijzonder is dat!
Het is natuurlijk wel interessant om te onderzoeken waar de trompet aan moet voldoen om tot deze kenmerken te komen.
Hiervoor stelde ik dat de diameter van de trompet iedere tien centimeter evenredig kleiner wordt, maar dit kan op
oneindig veel manieren.
Ik heb bovenstaande berekening gedaan voor deze trompetvorm:
Laat ik dit eens veralgemeniseren:
Het oppervlak wordt dan (waarbij ik wederom gebruik maak van de
tabel met integralen):
En het volume wordt:
Ik los deze
integraal eerst op voor het bijzondere
geval dat b = 0.5:
In alle andere gevallen wordt de oplossing:
Vervolgens ga ik de limietgevallen onderzoeken, eerst het volume voor b = 0.5:
Vervolgens kijk ik naar het volume voor b is ongelijk aan 0.5:
Die term waar L in voorkomt moet naar nul gaan voor L gaat naar oneindig.
Dat gebeurt alleen indien de exponent kleiner is dan nul, en dus voor b > 0.5:
Wat gebeurt er dan met het oppervlak?
Ik neem de eerste term van de somreeks, n = 0, even apart:
Voor b < 1 is het bij deze eerste term al een uitgemaakte zaak: het oppervlak gaat naar oneindig.
Voor n > 0 en L gaat naar oneindig wordt die term met L erin nul en is er wat extra onderzoek nodig:
Het is niet zo simpel om rechtstreeks een uitspraak te doen over wat deze reeks doet wanneer n naar oneindig gaat,
maar ik kan wel onderzoeken wat de grootte van een bepaalde term is ten opzichte van de voorgaande term.
Omdat ik alleen geïnteresseerd ben in de grootte van de termen (en niet in het teken) laat ik die macht van
−1 even weg:
Vervolgens kijk ik alleen naar grote waarden van n:
Voor b > 1 is iedere term groter dan de voorgaande term en divergeert de reeks en is het oppervlak oneindig.
Conclusie: voor b > 0.5 is het oppervlak altijd oneindig en het volume altijd eindig.
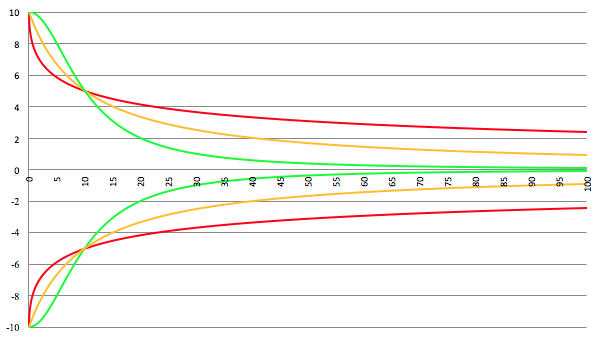
De grafiek van f (x) = 1/x
b voor b = 0.5 (de rode lijn),
b = 1 (de oranje lijn) en b = 2 (de groene lijn),
er zitten enkele transformaties in verwerkt om het begin van de trompet bij x = 0 te leggen,
de eenheid in centimeters weer te geven en de opening 20 cm te maken
Tijdens de bovenstaande berekening heb ik de vorm van de trompet op deze manier veralgemeniseerd:
Maar dat kan ook op deze manier:
De
afgeleide hiervan is:
Het oppervlak wordt dan (waarbij ik nogmaals gebruik maak van de
tabel met integralen):
En het volume wordt:
Vervolgens ga ik weer de limietgevallen onderzoeken, eerst het volume:
Die term waar L in voorkomt moet naar nul gaan voor L gaat naar oneindig.
Dat gebeurt alleen indien b > 1:
Wat gebeurt er dan met het oppervlak?
Voor b > 1 is zowel het volume als het oppervlak eindig.
Om een trompet te bouwen met een eindig volume en een oneindig oppervlak zal de vorm van de trompet daarom moeten voldoen aan:



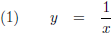
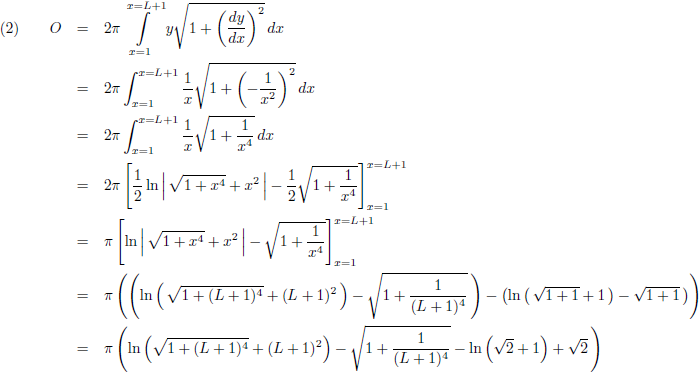
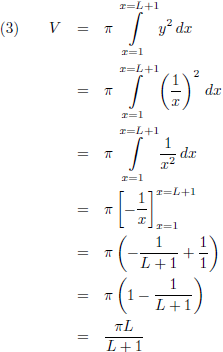
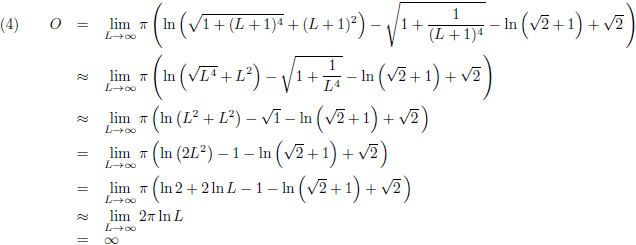
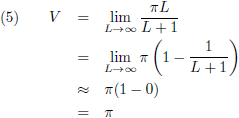
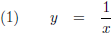
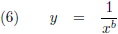
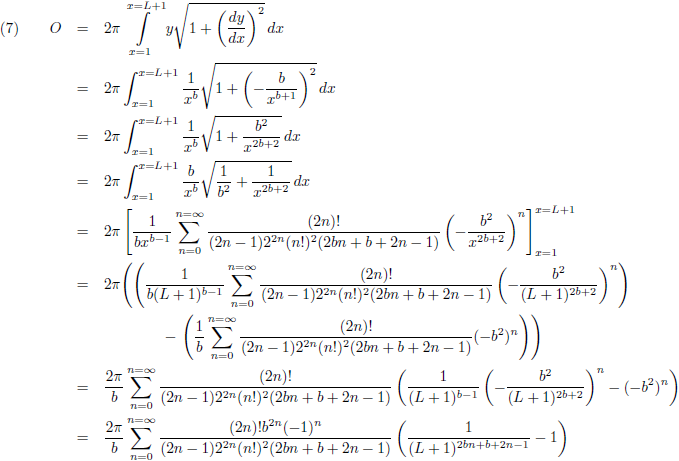
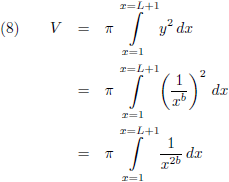
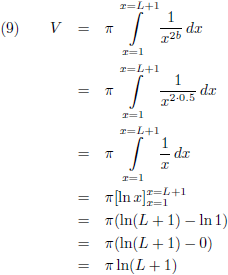
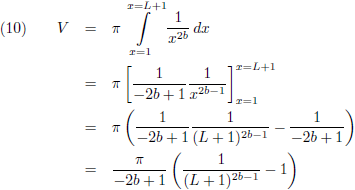
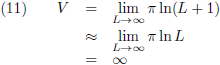
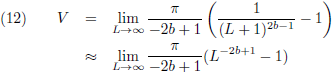
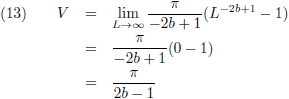
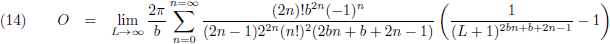
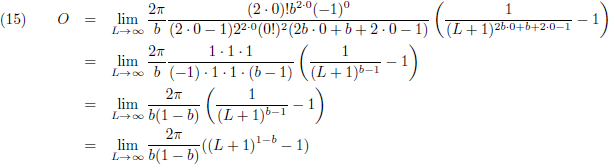
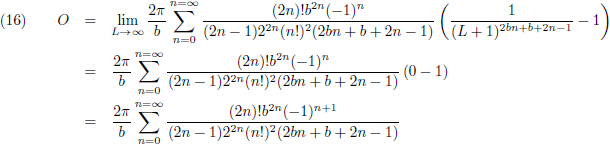
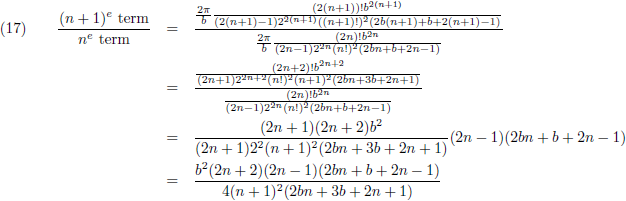
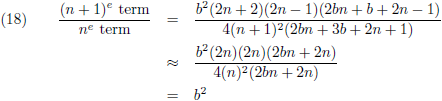

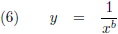
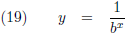
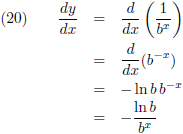
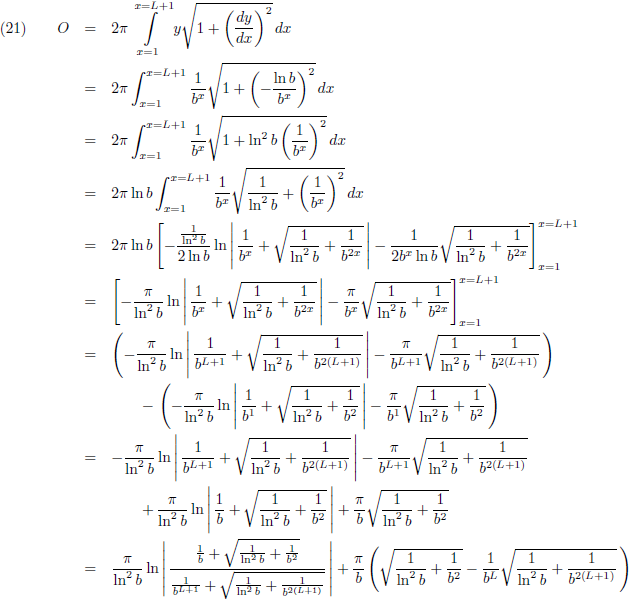
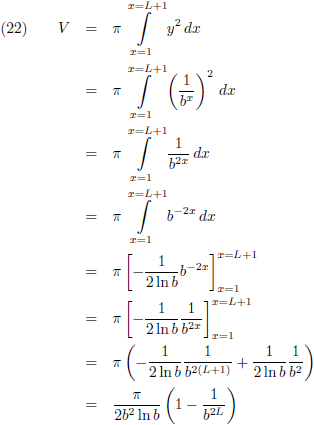
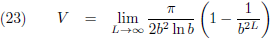
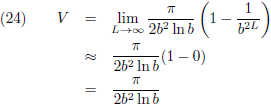
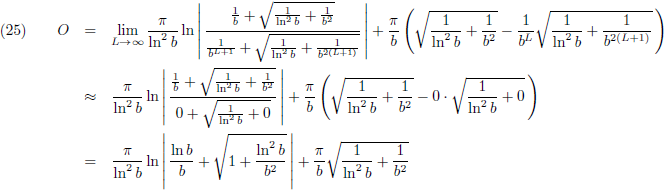
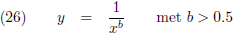

 Naar de overzichtspagina met bijzondere figuren
Naar de overzichtspagina met bijzondere figuren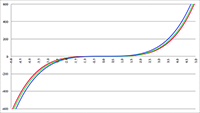 De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 29
Vectoren, vraagstuk 29 Vectoren, vraagstuk 67
Vectoren, vraagstuk 67 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van Boekhouden
Boekhouden Relativiteitstheorie rekenkundig, hoofdstuk 3: het balletje
Relativiteitstheorie rekenkundig, hoofdstuk 3: het balletje Uitleg artikel precessie van Mercurius: paragraaf 1
Uitleg artikel precessie van Mercurius: paragraaf 1 Eddington-Finkelstein-coördinaten
Eddington-Finkelstein-coördinaten De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt Fourier-analyse van het onzekerheidsprincipe van Heisenberg (II)
Fourier-analyse van het onzekerheidsprincipe van Heisenberg (II) De grote vragen in het leven
De grote vragen in het leven De illusie dat ik fout bezig ben
De illusie dat ik fout bezig ben De reis naar de werkelijkheid van Karel de Vlieger
De reis naar de werkelijkheid van Karel de Vlieger De Meezingnacht
De Meezingnacht De angst voor Liefde
De angst voor Liefde LaTeX
LaTeX Recent toegevoegde pagina’s
Recent toegevoegde pagina’s Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen