Alle symmetrieën van de Riemann-tensor
Toon alle symmetrieën van de Riemann-tensor aan.
Dit is de Riemann-tensor:
De Riemann-tensor volgens vergelijking (1) is gegeven in Christoffel-symbolen.
De definitie van de Christoffel-symbolen van de eerste soort is:
En de definitie van de Christoffel-symbolen van de tweede soort is:
Hieruit volgt:
Ik schrijf nu allereerst de Riemann-tensor in volledig covariante vorm:
Hiermee ga ik knutselen:
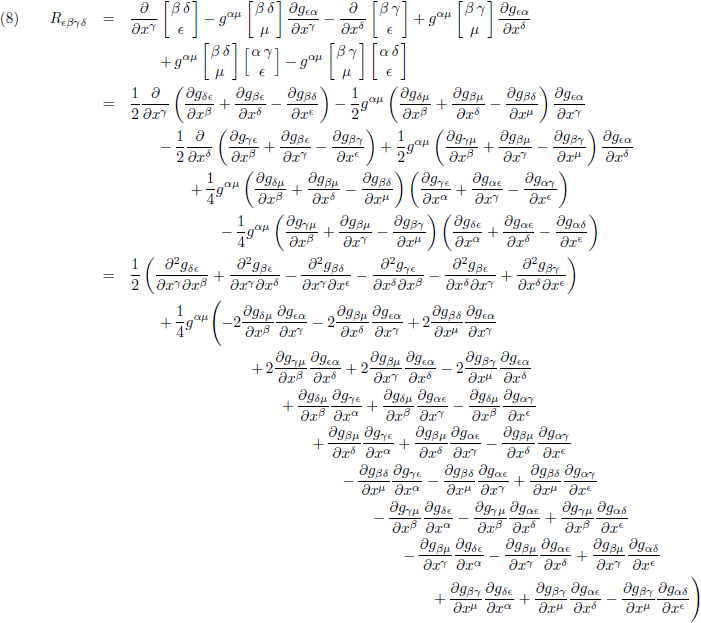
Met behulp van de vergelijkingen (3) en (4) kan ik vergelijking (6) verder verbouwen:
Om de chaos compleet te maken betrek ik vergelijking (2) erbij en ga ik vervolgens haakjes wegwerken:
Gelukkig is er ook goed nieuws, want we kunnen termen wegstrepen of samennemen:
Ik herschik de termen nog een beetje en ik zet ze onder elkaar:
Bij wat nu komen gaat moeten we de volgende zaken goed voor ogen houden:
- de metrische tensor is symmetrisch:
- de Christoffel-symbolen zijn symmetrisch in de eerste twee indices (de bovenindices):
- het maakt niet uit of ik ‘iets’ eerst naar de ene variabele differentieer
en daarna naar de andere of omgekeerd:
- dummy indices mag ik naar hartelust een andere naam geven.
Wat gebeurt er wanneer ik de eerste - en de tweede index van de Riemann-tensor verwissel:
De eerste conclusie is dat de Riemann-tensor anti-symmetrisch is in de eerste twee indices (symmetrisch betekent
dat je probleemloos twee indices mag verwisselen en anti-symmetrisch betekent dat bij verwisseling van twee
indices er een tekenwisseling plaatsvindt).
Wat gebeurt er wanneer ik de derde - en de vierde index verwissel:
De tweede conclusie is dat de Riemann-tensor ook anti-symmetrisch is in de laatste twee indices (dit volgt ook vrij
simpel uit de Riemann-tensor in gemengde vorm, zie
deze pagina).
Wat gebeurt er wanneer ik de eerste twee - en de laatste twee indices paarsgewijs verwissel:
De derde conclusie is dat de Riemann-tensor symmetrisch is in het eerste paar - en het tweede paar indices.
Samengevat:
Of omgekeerd:
Een logische vraag is natuurlijk (vind ik) of dit allemaal net zo uitpakt voor de gemengde vorm van de
Riemann-tensor, want ik heb deze symmetrieën immers afgeleid voor de Riemann-tensor in volledig covariante vorm
terwijl de Riemann-tensor in het ‘dagelijks gebruik’ in gemengde vorm langskomt.
Hiervoor kwam ik bijvoorbeeld als eerste tot de conclusie dat de covariante Riemann-tensor anti-symmetrisch is
in de eerste twee indices.
Wanneer ik dat rechtstreeks vertaal naar de Riemann-tensor in gemengde vorm dan zou dit de voorliggende vraag zijn:
Echter, op deze manier vergelijk ik appels met peren, omdat de indices α en β in het linkerlid en het
rechterlid op verschillende hoogte staan.
Kortom, dit is niet de goede vraag.
Ik moet de vraag zo stellen dat de indexnotatie klopt:
Dit is een zinvolle vraag.
Vervolgens verbouw ik de Riemann-tensor in het rechterlid naar de covariante vorm:
Door de eerste twee indices te verwisselen wisselt het teken als gevolg van de anti-symmetrie en ik knutsel nog
wat verder:
En zo klopt het inderdaad.
Vanaf vergelijking (17) had ik het ook als volgt kunnen doen:
Ook op deze manier klopt de anti-symmetrie waarbij de appels de appels en de peren de peren blijven.
De anti-symmetrie in de eerste twee indices kan ik ook op een andere manier voor het voetlicht brengen.
Indien ik de eerste twee indices aan elkaar gelijk stel dan moet er altijd nul uitkomen, want dat is het enige getal
dat anti-symmetrisch is ten opzichte van zichzelf (lees: zichzelf blijft na een tekenwisseling).
Dat ga ik laten zien en daarvoor ga ik de Riemann-tensor volledig uitschrijven in componenten van
de metrische tensor door vergelijking (3) in te vullen in vergelijking (1) en vervolgens de boel
wat te reorganiseren:
Ik kan twee termen tegen elkaar wegstrepen:
Vervolgens stel ik β gelijk aan α:
Nu is α ook een dummy index geworden en mag ik die, per term, naar believen verwisselen met een andere
dummy index.
En dit geldt natuurlijk ook voor de andere dummy indices onderling.
Het is een enorm gepuzzel, maar uiteindelijk ontstaat er dit:
Nu kan ik bijna alle termen tegen elkaar wegstrepen:
Met deze kennis in ons achterhoofd:
En omdat:
Hiermee wordt vergelijking (25):
Dit resultaat stop ik in vergelijking (24):
Ik verwissel de dummy indices in de linkerterm:
Waarmee bewezen is dat er anti-symmetrie is in de eerste twee indices.
De tweede conclusie was dat de Riemann-tensor anti-symmetrisch is in de laatste twee indices,
en zoals reeds gezegd volgt dit ook vrij simpel uit de Riemann-tensor in gemengde vorm
(zie
deze pagina).
Tot slot de symmetrie van de paarsgewijze verwisseling van de eerste twee - en de laatste twee indices.
Dat leidt tot deze vraag:
Ook deze vraagstelling leidt tot een conflict tussen de appels en de peren.
Ik moet wederom de vraag zo stellen dat de indexnotatie klopt:
Dit is weer een zinvolle vraag.
Nu wordt het een herhaling van zetten, ik verbouw de Riemann-tensor in het rechterlid naar de covariante vorm en ik
ga knutselen:
Dat brengt ons bij dit overzicht:
| Symmetrieën in de Riemann-tensor |
| Gemengde vorm |
Covariante vorm |
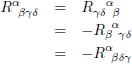 |
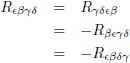 |
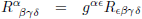 |
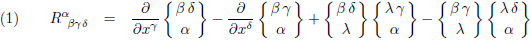
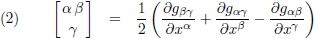
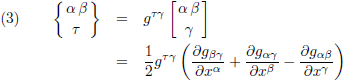
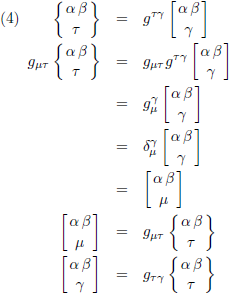
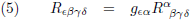
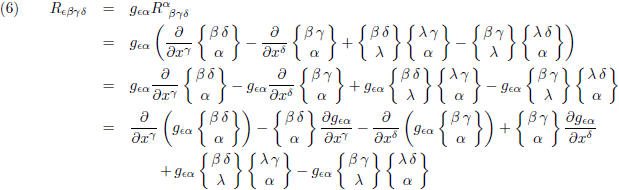
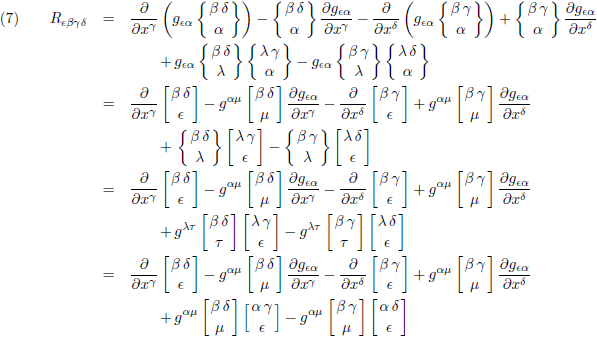

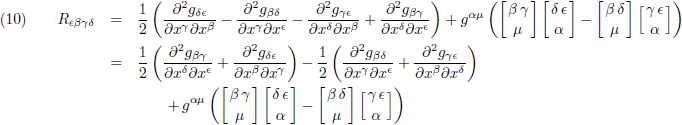
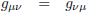
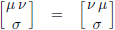
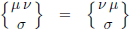
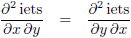
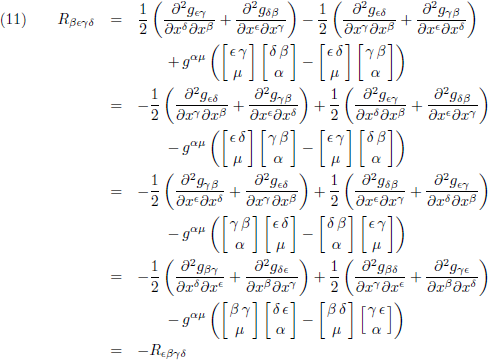
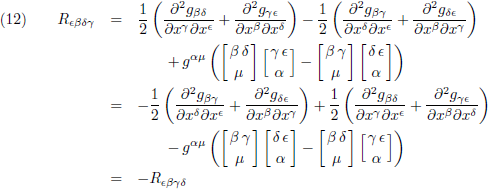
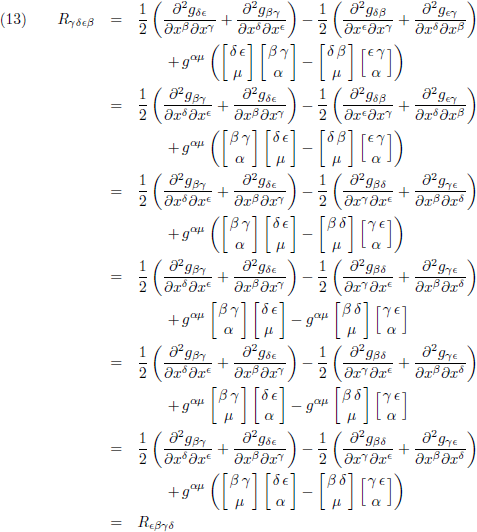
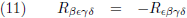
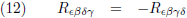
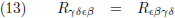
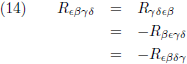
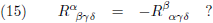
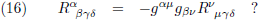
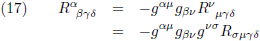
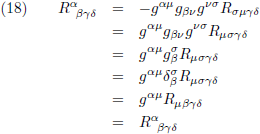
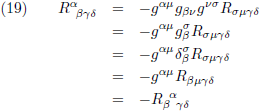

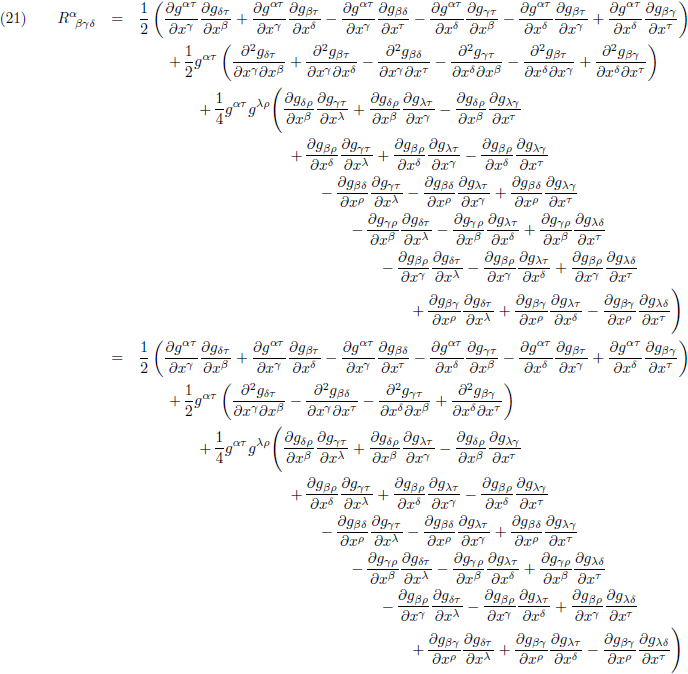
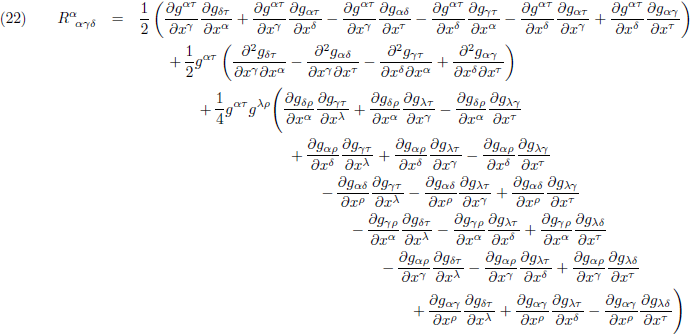

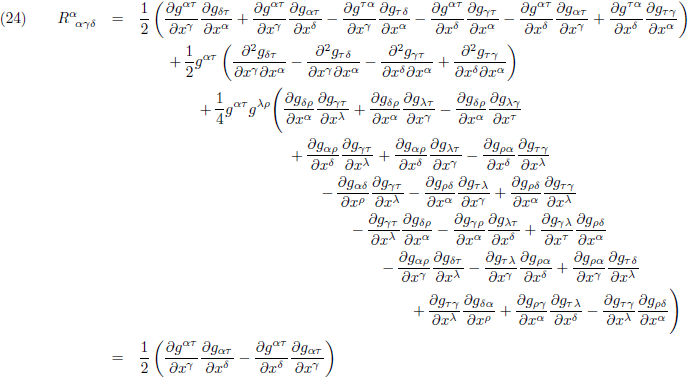
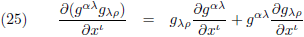
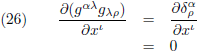
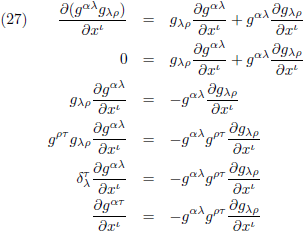
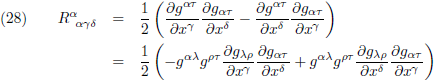
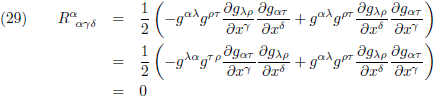
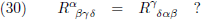
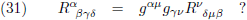
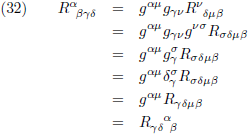
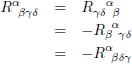
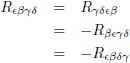
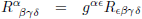


 Door naar het volgende vraagstuk: mathematisch verschillende componenten in de Riemann-tensor
Door naar het volgende vraagstuk: mathematisch verschillende componenten in de Riemann-tensor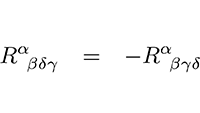 Terug naar het vorige vraagstuk: anti-symmetrie in de Riemann-tensor
Terug naar het vorige vraagstuk: anti-symmetrie in de Riemann-tensor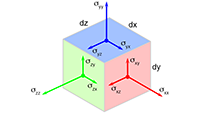 Naar de overzichtspagina met vraagstukken
Naar de overzichtspagina met vraagstukken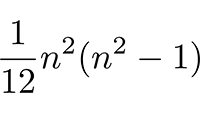 Onafhankelijke componenten in de Riemann-tensor
Onafhankelijke componenten in de Riemann-tensor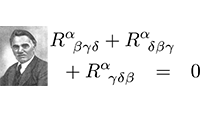 De Bianchi-identiteit
De Bianchi-identiteit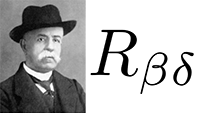 Hoe vormt zich de Ricci-tensor?
Hoe vormt zich de Ricci-tensor? Hoe vormt zich de Ricci-scalar?
Hoe vormt zich de Ricci-scalar? De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integralen van
De integralen van Vectoren, vraagstuk 19
Vectoren, vraagstuk 19 Vectoren, vraagstuk 57
Vectoren, vraagstuk 57 Vectoren, vraagstuk 95
Vectoren, vraagstuk 95 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid
Relativiteitstheorie basic, hoofdstuk 2: de lichtsnelheid Uitleg artikel algemene relativiteitstheorie: paragraaf 17
Uitleg artikel algemene relativiteitstheorie: paragraaf 17 De SuperLamborghini
De SuperLamborghini Ruimtetijdkromming
Ruimtetijdkromming Het traagheidsmoment van de Zon
Het traagheidsmoment van de Zon Vraagstukken algemene natuurkunde
Vraagstukken algemene natuurkunde Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen