De integraal van
f (x) = 1/(ax3 + bx2 + cx + d)1/2
Trefwoorden/keywords: integraal/integral, integreren/integrate, f (x) = 1/(ax3 + bx2 + cx + d)1/2
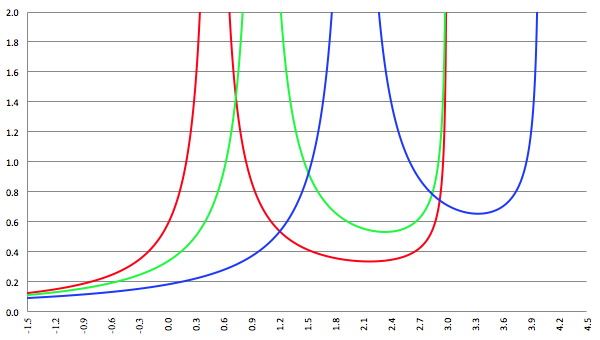
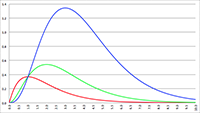
De grafiek van f (x) = 1/(ax
3 + bx
2 + cx + d)
1/2 voor a = −4, b = 16, c = −13, d = 3 (de rode lijn),
a = −3, b = 15, c = −21, d = 9 (de groene lijn) en a = −2, b = 16, c = −40, d = 32 (de blauwe lijn)
Gegeven is dat a < 0, dus die
derdegraads vergelijking in de noemer
‘begint’ ergens linksboven (in het tweede kwadrant) en ‘eindigt’ ergens rechtsonder (in het vierde kwadrant).
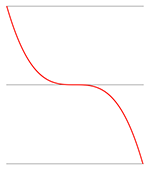
a < 0 |
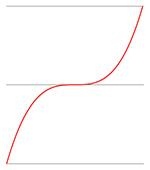
a > 0 |
Verder is gegeven dat de
discriminant D nul is,
dus er zijn twee nulpunten.
Voor de duidelijkheid maak ik een grafiek van alleen de
derdegraads vergelijking.
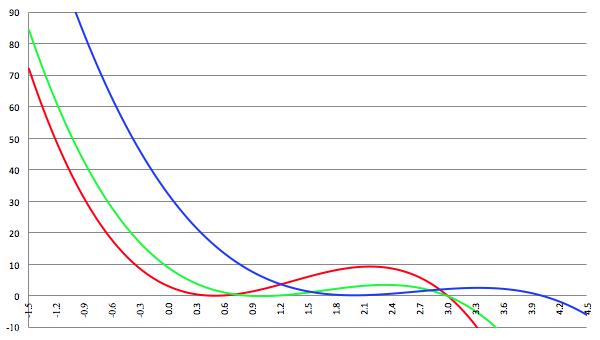
De grafiek van f (x) = ax
3 + bx
2 + cx + d voor a = −4, b = 16, c = −13, d = 3 (de rode lijn),
a = −3, b = 15, c = −21, d = 9 (de groene lijn) en a = −2, b = 16, c = −40, d = 32 (de blauwe lijn)
Ik zal ook nog even verticaal inzoomen in de buurt van de horizontale as.
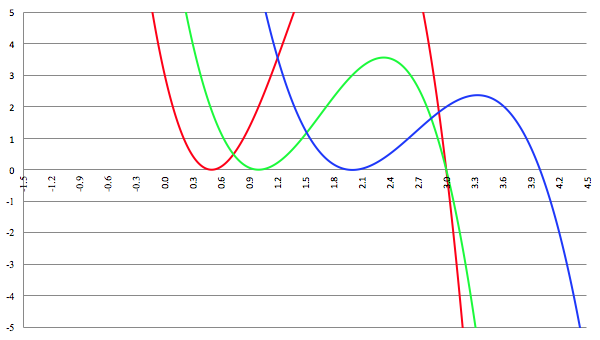
De grafiek van f (x) = ax
3 + bx
2 + cx + d voor a = −4, b = 16, c = −13, d = 3 (de rode lijn),
a = −3, b = 15, c = −21, d = 9 (de groene lijn) en a = −2, b = 16, c = −40, d = 32 (de blauwe lijn)
Om te beginnen ga ik die
derdegraads vergelijking normaliseren:
Ik stel:
Hiermee wordt de functie:
Ik haal er even een hulpvariabele bij:
De
discriminant is nul, dus er zijn twee nulpunten.
Of preciezer gezegd: twee nulpunten vallen samen en vormen een raakpunt.
Die kan ik als volgt berekenen (x
1 is het snijpunt, x
2 is het raakpunt):
Het verschil van x
2 en x
1 is:
Omdat q'' negatief is, is het verschil van x
2 en x
1 ook negatief.
Het raakpunt x
2 ligt dus links van het snijpunt x
1.
De
integraal wordt dan:
Nu ga ik het hele boeltje verschuiven zodat het raakpunt in de oorsprong komt te liggen.
Ik stel:
Hiermee wordt de
integraal:
Voor de
integraal heb ik 1/√a staan,
maar dat kan helemaal niet omdat a negatief is.
Dat ga ik nu repareren:
De oplossing van de
integraal van
1/(x (ax + b)
1/2) kun je elders vinden in de
tabel met integralen
(de plusmintekens verschijnen in verband met de
absolute waarde van u).
Dat brengt ons bij dit tussenresultaat:
Nu moet u uiteraard weer vervangen worden door x:
Ter controle ga ik het resultaat
differentiëren:
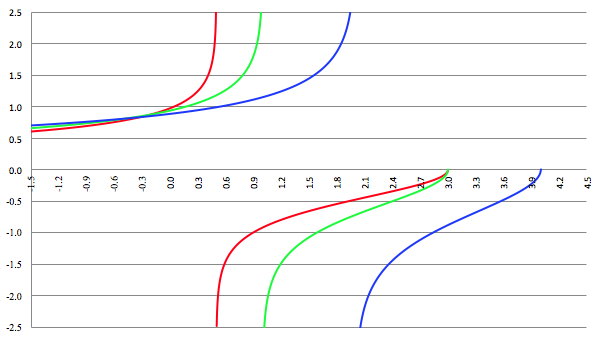
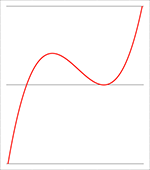
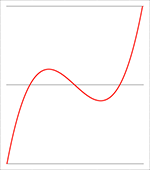
De grafiek van F (x) voor a = −4, b = 16, c = −13, d = 3 (de rode lijn),
a = −3, b = 15, c = −21, d = 9 (de groene lijn)
en a = −2, b = 16, c = −40, d = 32 (de blauwe lijn), C = 0
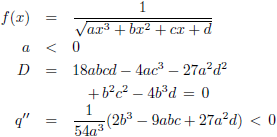





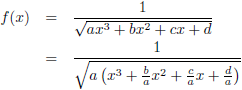
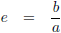
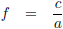

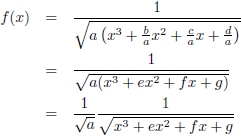
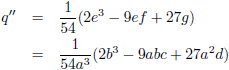
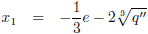
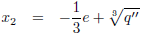
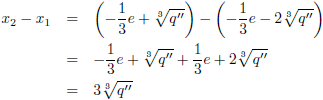
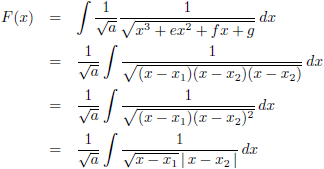
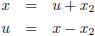
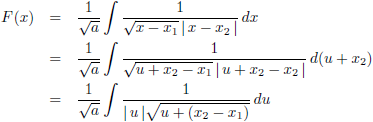
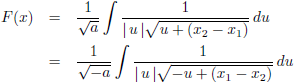
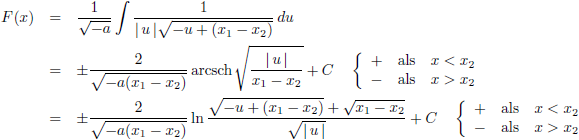
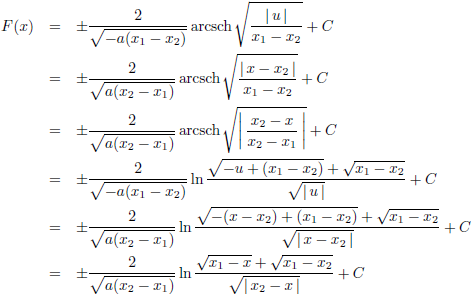
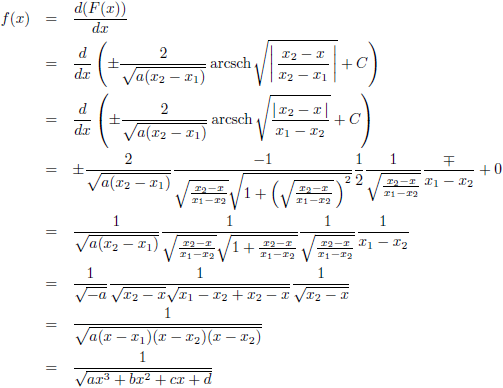

 Door naar de volgende integraal: de integraal van
Door naar de volgende integraal: de integraal van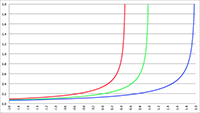 Terug naar de vorige integraal: de integraal van
Terug naar de vorige integraal: de integraal van Tabel met integralen
Tabel met integralen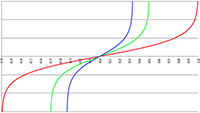 Tabel met afgeleiden
Tabel met afgeleiden Tabel met Taylor-reeksen
Tabel met Taylor-reeksen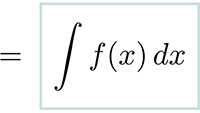 Integreren
Integreren Differentiëren
Differentiëren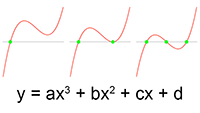 Derdegraads vergelijking oplossen
Derdegraads vergelijking oplossen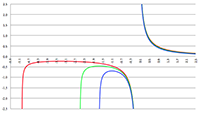 De integraal van
De integraal van Wiskunde algemeen
Wiskunde algemeen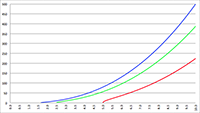 De integraal van
De integraal van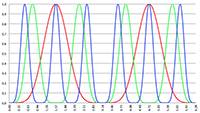 De integraal van
De integraal van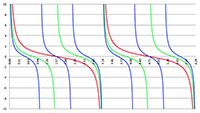 De integraal van
De integraal van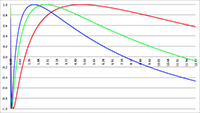 De integraal van
De integraal van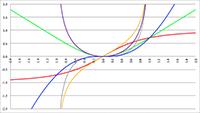 De integralen van
De integralen van Vectoren, vraagstuk 71
Vectoren, vraagstuk 71 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT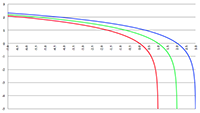 De Taylor-reeks van
De Taylor-reeks van De Taylor-reeks van
De Taylor-reeks van Lijnen trekken door negen punten
Lijnen trekken door negen punten Relativiteitstheorie rekenkundig, hoofdstuk 7: kromming
Relativiteitstheorie rekenkundig, hoofdstuk 7: kromming Relativistische slakken
Relativistische slakken De relativistische rotatie-energie van een massieve bol
De relativistische rotatie-energie van een massieve bol Astronomie
Astronomie Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen