De integraal van
f (x) = 1/(ax3 + bx2 + cx + d)1/2
Trefwoorden/keywords: integraal/integral, integreren/integrate, f (x) = 1/(ax3 + bx2 + cx + d)1/2
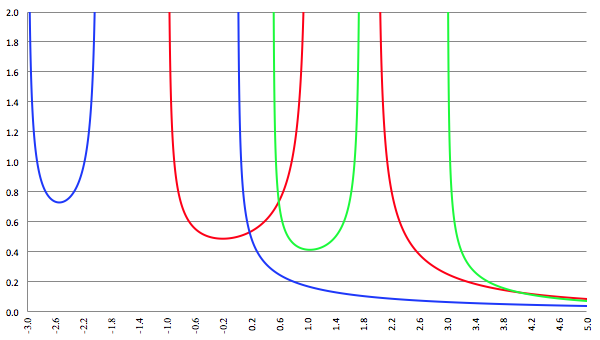
De grafiek van f (x) = 1/(ax
3 + bx
2 + cx + d)
1/2 voor a = 2, b = −4, c = −2, d = 4 (de rode lijn),
a = 8, b = −42, c = 61, d = −21 (de groene lijn) en a = 3, b = 15, c = 18, d = 0 (de blauwe lijn)
Gegeven is dat a > 0, dus die
derdegraads vergelijking in de noemer
‘begint’ ergens linksonder (in het derde kwadrant) en ‘eindigt’ ergens rechtsboven (in het eerste kwadrant).
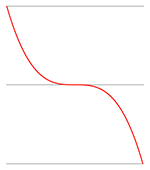
a < 0 |
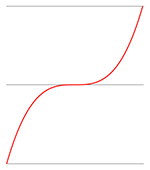
a > 0 |
Verder is gegeven dat de
discriminant D positief is,
dus er zijn drie nulpunten.
Voor de duidelijkheid maak ik een grafiek van alleen de
derdegraads vergelijking.
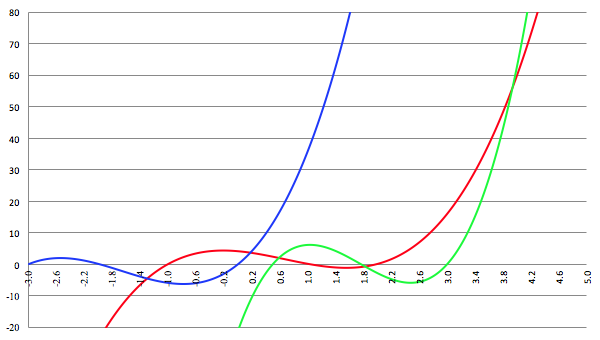
De grafiek van f (x) = ax
3 + bx
2 + cx + d voor a = 2, b = −4, c = −2, d = 4 (de rode lijn),
a = 8, b = −42, c = 61, d = −21 (de groene lijn) en a = 3, b = 15, c = 18, d = 0 (de blauwe lijn)
Ik zal ook nog even verticaal inzoomen in de buurt van de horizontale as.
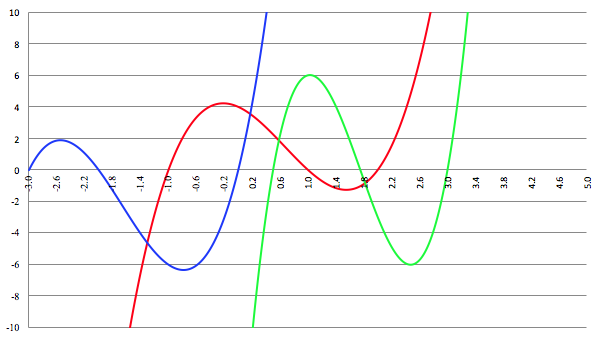
De grafiek van f (x) = ax
3 + bx
2 + cx + d voor a = 2, b = −4, c = −2, d = 4 (de rode lijn),
a = 8, b = −42, c = 61, d = −21 (de groene lijn) en a = 3, b = 15, c = 18, d = 0 (de blauwe lijn)
Voor het oplossen van deze
integraal
maken we maximaal gebruik van de trucendoos.
Om te beginnen ga ik die
derdegraads vergelijking normaliseren:
Ik stel:
Hiermee wordt de functie:
Ik haal er even wat hulpvariabelen bij:
De
discriminant is positief, dus er zijn drie nulpunten.
Die kan ik als volgt berekenen (van links naar rechts, dus x
1 < x
2 < x
3):
Hiermee wordt de functie:
De
integraal wordt dan:
Nu ga ik het hele boeltje verschuiven zodat het linkernulpunt in de oorsprong komt te liggen.
Ik stel:
Hiermee wordt de
integraal:
Vervolgens stel ik:
Hiermee wordt de
integraal:
Ik ga gebruik maken van
goniometrische substitutie door secans of cosecans:
Hiermee wordt de integraal:
Ik stel:
Hiermee wordt de
integraal:
Deze
integraal
staat te boek als de elliptische integraal van de eerste soort.
De oplossing van die
integraal
kun je elders vinden in de
tabel met integralen:
Nu moet t uiteraard weer vervangen worden door x:
En ik ga h anders opschrijven:
Die eerste term van het antwoord neem ik ook nog even onder handen:
Om het uiteindelijke antwoord op te schrijven neem ik de reeks met al die
sinussen, want die convergeert het beste:
Om te voorkomen dat je tegen de grenzen van je rekenprogramma aanloopt is het wel handig om niet
iedere term opnieuw te berekenen, maar ten opzichte van de voorgaande term:
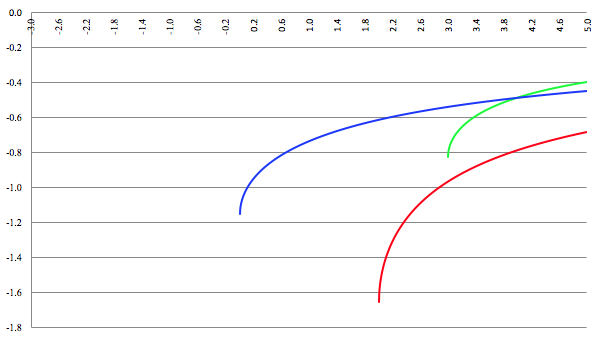
De grafiek van F (x) voor a = 2, b = −4, c = −2, d = 4 (de rode lijn),
a = 8, b = −42, c = 61, d = −21 (de groene lijn) en a = 3, b = 15, c = 18, d = 0 (de blauwe lijn), C = 0,
10 termen meegenomen
Voor het maken van de bovenstaande grafiek heb ik tien termen meegenomen en dan is het even goed opletten of dat wel genoeg is.
Daarom maak ik de grafiek nogmaals, maar dan met tien termen extra.
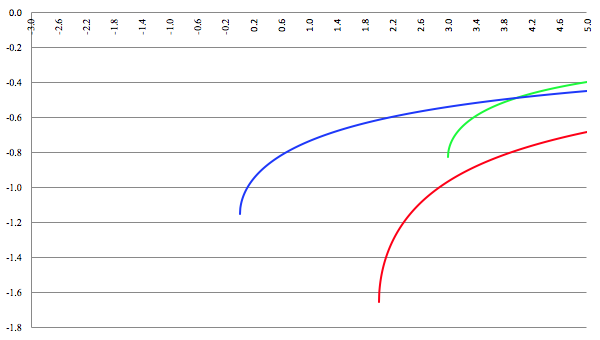
De grafiek van F (x) voor a = 2, b = −4, c = −2, d = 4 (de rode lijn),
a = 8, b = −42, c = 61, d = −21 (de groene lijn) en a = 3, b = 15, c = 18, d = 0 (de blauwe lijn), C = 0,
20 termen meegenomen
Voor de duidelijkheid leg ik de beide voorgaande grafieken over elkaar heen (met een ander kleurtje).
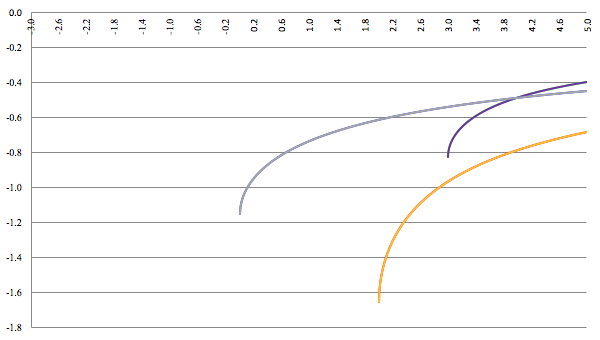
De grafiek van F (x) voor a = 2, b = −4, c = −2, d = 4 (de rode lijn),
a = 8, b = −42, c = 61, d = −21 (de groene lijn) en a = 3, b = 15, c = 18, d = 0 (de blauwe lijn), C = 0,
10 termen meegenomen,
de grafiek van F (x) voor a = 2, b = −4, c = −2, d = 4 (de oranje lijn),
a = 8, b = −42, c = 61, d = −21 (de paarse lijn) en a = 3, b = 15, c = 18, d = 0 (de grijze lijn), C = 0,
20 termen meegenomen
De grafieken zijn in dit geval identiek, dus tien termen meenemen is voldoende.
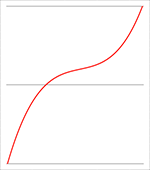
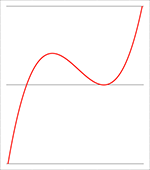
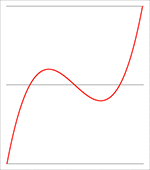
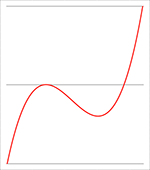
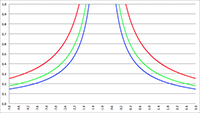
De problemen ontstaan wanneer twee nulpunten dicht bij elkaar in de buurt komen, want dan ontstaat een van beide onderstaande
situaties en moeten er heel veel meer termen meegenomen worden om tot een nauwkeurig antwoord te komen.
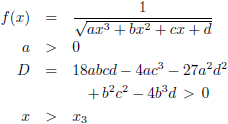





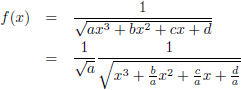
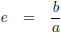
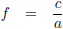

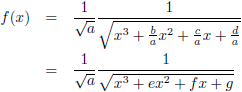
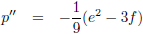
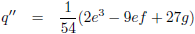
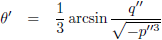
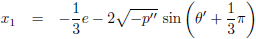
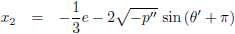
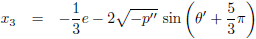
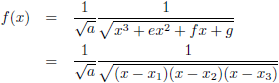
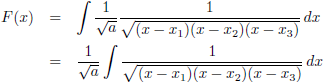
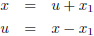
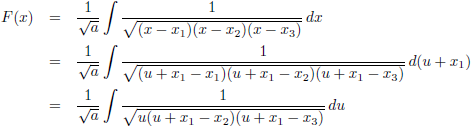
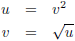
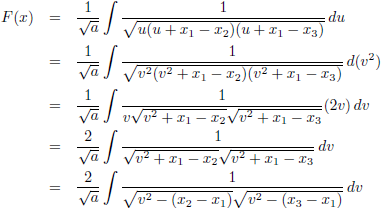
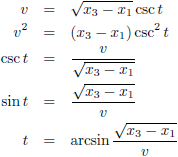
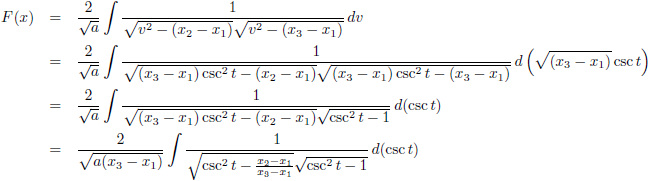
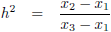
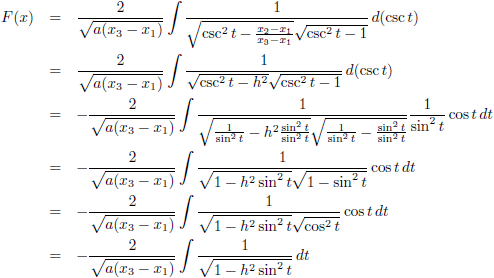
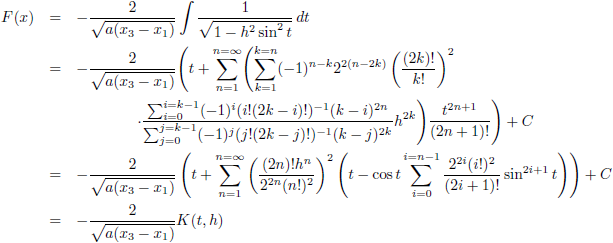
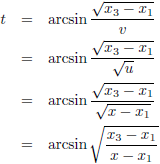
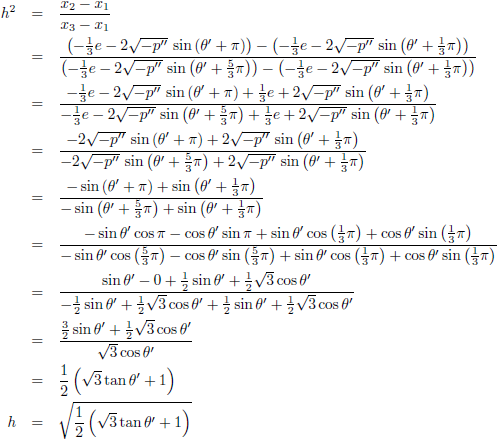
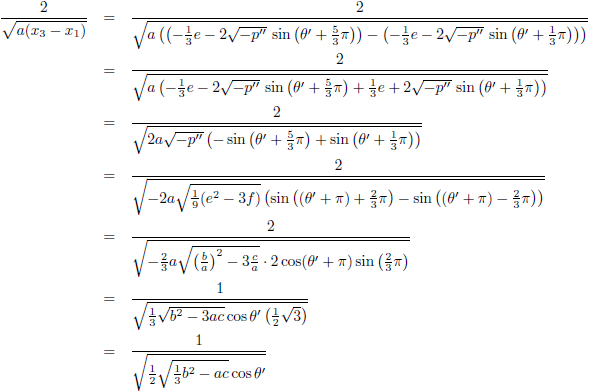
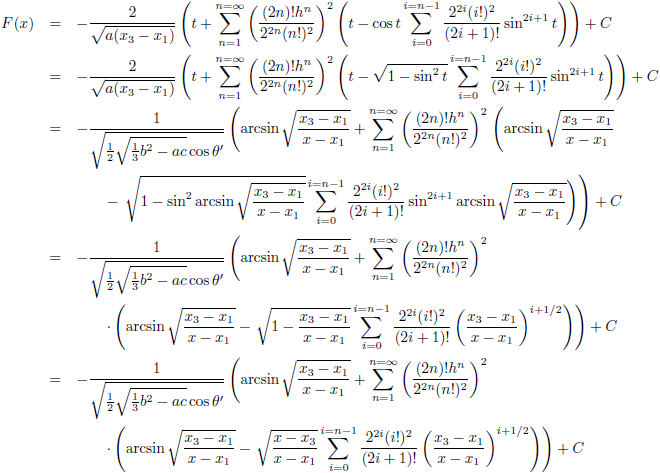






 Door naar de volgende integraal: de integraal van
Door naar de volgende integraal: de integraal van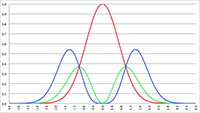 Terug naar de vorige integraal: de integraal van
Terug naar de vorige integraal: de integraal van Tabel met integralen
Tabel met integralen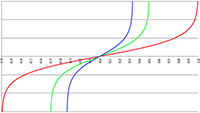 Tabel met afgeleiden
Tabel met afgeleiden Tabel met Taylor-reeksen
Tabel met Taylor-reeksen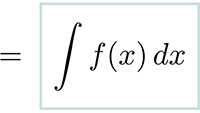 Integreren
Integreren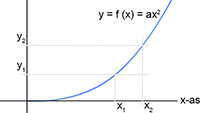 Differentiëren
Differentiëren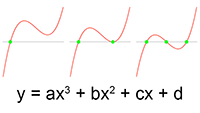 Derdegraads vergelijking oplossen
Derdegraads vergelijking oplossen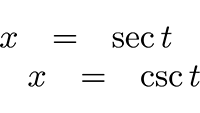 Goniometrische substitutie door secans of cosecans
Goniometrische substitutie door secans of cosecans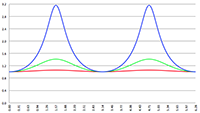 De integraal van
De integraal van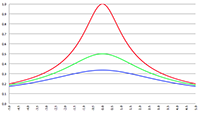 De integraal van
De integraal van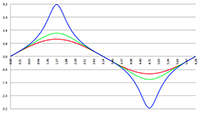 De integraal van
De integraal van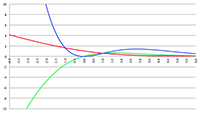 De integraal van
De integraal van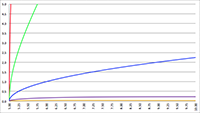 De integralen van
De integralen van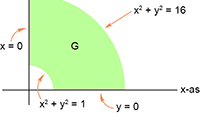 Vectoren, vraagstuk 24
Vectoren, vraagstuk 24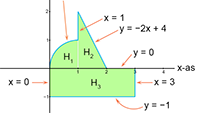 Vectoren, vraagstuk 62
Vectoren, vraagstuk 62 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT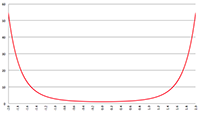 De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 7: kromming
Relativiteitstheorie basic, hoofdstuk 7: kromming Uitleg artikel algemene relativiteitstheorie: paragraaf 21
Uitleg artikel algemene relativiteitstheorie: paragraaf 21 Afleiding van de Reissner-Nordström-oplossing
Afleiding van de Reissner-Nordström-oplossing Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen