Error 404: Not Found

Oeps! En toen was je ineens waar je niet wezen wilde!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
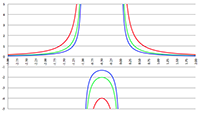 De integraal van
De integraal van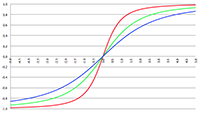 De integraal van
De integraal van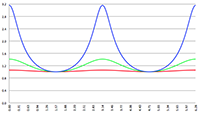 De integraal van
De integraal van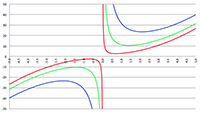 De integraal van
De integraal van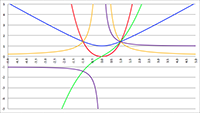 De integralen van
De integralen van Vectoren, vraagstuk 25
Vectoren, vraagstuk 25 Vectoren, vraagstuk 63
Vectoren, vraagstuk 63 Vraagstukken xref voor de UT
Vraagstukken xref voor de UT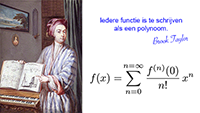 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen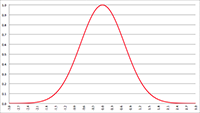 De Taylor-reeks van
De Taylor-reeks van De stelling van Stokes
De stelling van Stokes Relativiteitstheorie basic, hoofdstuk 8: nabeschouwingen
Relativiteitstheorie basic, hoofdstuk 8: nabeschouwingen Uitleg artikel algemene relativiteitstheorie: paragraaf 22
Uitleg artikel algemene relativiteitstheorie: paragraaf 22 Een geodetische lijn rondom een puntmassa
Een geodetische lijn rondom een puntmassa De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt Vraagstukken kwantummechanica
Vraagstukken kwantummechanica De Boltzmann-verdeling
De Boltzmann-verdeling De illusie van pijn en lijden
De illusie van pijn en lijden De reis naar de werkelijkheid van Danny Mekić
De reis naar de werkelijkheid van Danny Mekić De BAG-controle
De BAG-controle De Natuur spreekt: Flower/Bloem
De Natuur spreekt: Flower/Bloem LaTeX
LaTeX LaTeX code
LaTeX code Kalender van de jaren 0221 − 0230 met weekdagen
Kalender van de jaren 0221 − 0230 met weekdagen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt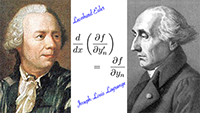 De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat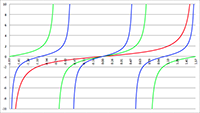 De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax)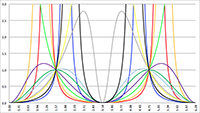 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2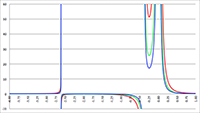 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen