Error 404: Not Found

Oeps! En toen was je ineens waar je niet wezen wilde!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
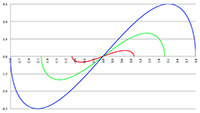 De integraal van
De integraal van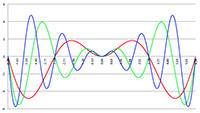 De integraal van
De integraal van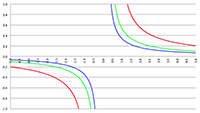 De integraal van
De integraal van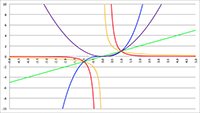 De integralen van
De integralen van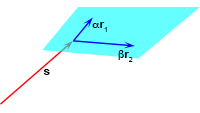 Vectoren, vraagstuk 3
Vectoren, vraagstuk 3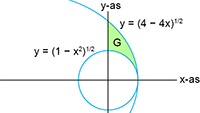 Vectoren, vraagstuk 41
Vectoren, vraagstuk 41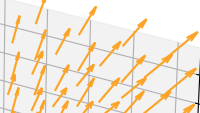 Vectoren, vraagstuk 79
Vectoren, vraagstuk 79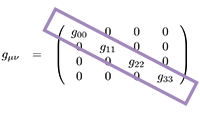 De diagonale metrische tensor, covariant en contravariant
De diagonale metrische tensor, covariant en contravariant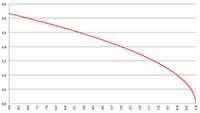 De Taylor-reeks van
De Taylor-reeks van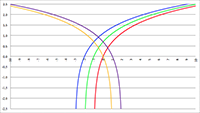 De Taylor-reeksen van
De Taylor-reeksen van De stelling van Green
De stelling van Green Uitleg artikel algemene relativiteitstheorie: paragraaf 2
Uitleg artikel algemene relativiteitstheorie: paragraaf 2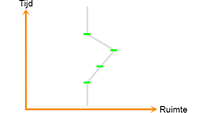 Het tekenen van een wereldlijn
Het tekenen van een wereldlijn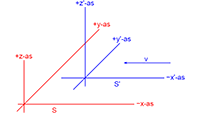 Lorentz-transformaties zonder invariantie van de lichtsnelheid
Lorentz-transformaties zonder invariantie van de lichtsnelheid Vraagstukken astronomie
Vraagstukken astronomie Het magnetische veld in een rechte spoel
Het magnetische veld in een rechte spoel Grijp jij je kansen?
Grijp jij je kansen? De illusie dat ik iets te verliezen heb
De illusie dat ik iets te verliezen heb De betekenis van relativiteit
De betekenis van relativiteit De puzzel
De puzzel Reacties op lezingen
Reacties op lezingen LaTeX
LaTeX Kalender van de jaren 0001 − 0010 met weekdagen
Kalender van de jaren 0001 − 0010 met weekdagen Kalender van de jaren 0381 − 0390 met weekdagen
Kalender van de jaren 0381 − 0390 met weekdagen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen