Error 404: Not Found

Oeps! En toen was je ineens waar je niet wezen wilde!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
 De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van De integraal van
De integraal van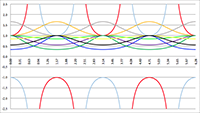 De integralen van
De integralen van Vectoren, vraagstuk 74
Vectoren, vraagstuk 74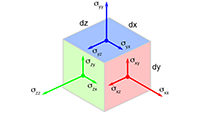 Vraagstukken tensoren
Vraagstukken tensoren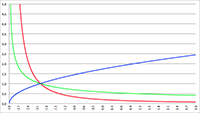 De Taylor-reeks van
De Taylor-reeks van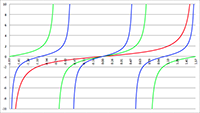 De Taylor-reeks van
De Taylor-reeks van Het probleem van de gevangenen
Het probleem van de gevangenen Uitleg artikel E = mc2
Uitleg artikel E = mc2 Een raket, een tunnel en twee kanonnen
Een raket, een tunnel en twee kanonnen Klassiek als limietgeval van relativistisch
Klassiek als limietgeval van relativistisch Astronomie
Astronomie Elektriciteit en magnetisme
Elektriciteit en magnetisme Zou je als kind geïnspireerd zijn?
Zou je als kind geïnspireerd zijn? De illusie van verbinding (I)
De illusie van verbinding (I) Vertellingen
Vertellingen Babies, wiskunde en Geert Wilders
Babies, wiskunde en Geert Wilders Reacties op lezingen
Reacties op lezingen LaTeX
LaTeX Cookiebeleid
Cookiebeleid Kalender van de jaren 0331 − 0340 met weekdagen
Kalender van de jaren 0331 − 0340 met weekdagen Kalender van de jaren 0711 − 0720 met weekdagen
Kalender van de jaren 0711 − 0720 met weekdagen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt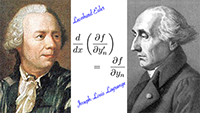 De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat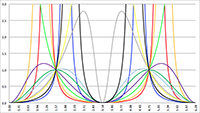 De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2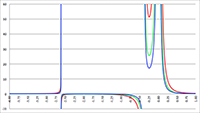 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen