Error 404: Not Found

Oeps! En toen was je ineens waar je niet wezen wilde!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
Maak je keuze in het menu om vrolijk verder te gaan op deze website.
Excuses voor het ongemak!
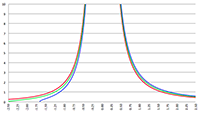 De integraal van
De integraal van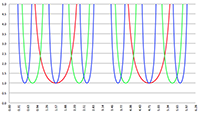 De integraal van
De integraal van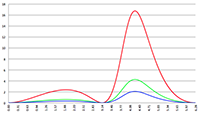 De integraal van
De integraal van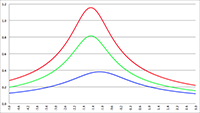 De integraal van
De integraal van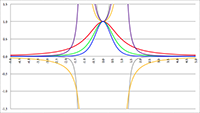 De integralen van
De integralen van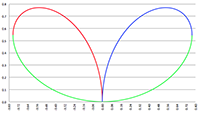 Vectoren, vraagstuk 60
Vectoren, vraagstuk 60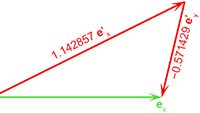 Bereken de covariante - en contravariante componenten
Bereken de covariante - en contravariante componenten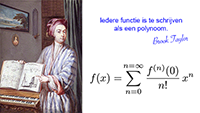 Tabel met Taylor-reeksen
Tabel met Taylor-reeksen De Taylor-reeks van
De Taylor-reeks van De stelling van Gauss
De stelling van Gauss Relativiteitstheorie basic, hoofdstuk 5: versnelling
Relativiteitstheorie basic, hoofdstuk 5: versnelling Uitleg artikel algemene relativiteitstheorie: paragraaf 19
Uitleg artikel algemene relativiteitstheorie: paragraaf 19 Afleiding van de Schwarzschild-oplossing
Afleiding van de Schwarzschild-oplossing De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Kwantummechanica
Kwantummechanica Oplossing voor de algemene golfvergelijking
Oplossing voor de algemene golfvergelijking De illusie van de recessie
De illusie van de recessie De reis naar de werkelijkheid van Tenzin Gyatso (de 14e Dalai Lama)
De reis naar de werkelijkheid van Tenzin Gyatso (de 14e Dalai Lama) Bruiloft in Marokko
Bruiloft in Marokko De Natuur spreekt: Water
De Natuur spreekt: Water LaTeX
LaTeX LaTeX code
LaTeX code Kalender van de jaren 0191 − 0200 met weekdagen
Kalender van de jaren 0191 − 0200 met weekdagen Kalender van de jaren 0571 − 0580 met weekdagen
Kalender van de jaren 0571 − 0580 met weekdagen Voorbeelden van E = mc2
Voorbeelden van E = mc2 De pijn die je voelt wanneer je in een zwart gat valt
De pijn die je voelt wanneer je in een zwart gat valt De versnelling van een baksteen die in een zwart gat valt
De versnelling van een baksteen die in een zwart gat valt De snelheid van een baksteen die in een zwart gat valt
De snelheid van een baksteen die in een zwart gat valt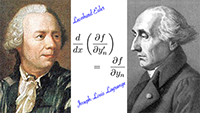 De Euler-Lagrange-vergelijking
De Euler-Lagrange-vergelijking De baan van een baksteen bij een zwart gat
De baan van een baksteen bij een zwart gat De Taylor-reeks van f (x) = tan (ax)
De Taylor-reeks van f (x) = tan (ax) De integralen van f (x) = sin2 x/(1 + a cos x)2
De integralen van f (x) = sin2 x/(1 + a cos x)2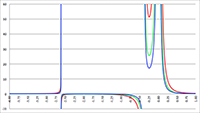 De integraal van f (x) = 1/(x2 (ax2 + bx + c))
De integraal van f (x) = 1/(x2 (ax2 + bx + c)) De invaltijd van een baksteen die in een zwart gat valt
De invaltijd van een baksteen die in een zwart gat valt Naar de overzichtspagina wiskunde
Naar de overzichtspagina wiskunde Naar de overzichtspagina natuurkunde
Naar de overzichtspagina natuurkunde Naar de overzichtspagina filosofie
Naar de overzichtspagina filosofie Doneer enkele euro’s
Doneer enkele euro’s Wetenschappelijke boeken te koop
Wetenschappelijke boeken te koop Lezingen
Lezingen